Адаптивная система с нечетким регулятором.
Похожие статьи вашей тематики
Рассматриваемая в этом параграфе АдСУ с нечетким регулятором (НР) следует отнести к адаптивным системам прямого подхода, поскольку в ней отсутствует процедура идентификации. Функциональная блок-схема АдСУ с НР показана на рис. 2.6 [20].

Рис 2.6
Объект управления является неопределенным и нелинейным, его параметры изменяются в процессе функционирования. Для поддержания заданного качества управления параметры НР составляющие вектора  изменяются синхронно (с некоторой инерционностью) с изменением параметров ОУ. Необходимое значение составляющих изменяются синхронно (с некоторой инерционностью) с изменением параметров ОУ. Необходимое значение составляющих  определяется в блоке адаптации (АА) на основании информации о значении ошибки определяется в блоке адаптации (АА) на основании информации о значении ошибки  и ее производной и ее производной  в основном контуре управления. Блок АА содержит процедуру дифференцирования в основном контуре управления. Блок АА содержит процедуру дифференцирования  и процедуру определения значений составляющих вектора и процедуру определения значений составляющих вектора  , на основании аналитического выражения закона адаптации. Желаемое качество управления в системе определяется критерием оптимизации , на основании аналитического выражения закона адаптации. Желаемое качество управления в системе определяется критерием оптимизации  относительно переменных состояния объекта вектора относительно переменных состояния объекта вектора  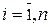 . Такая постановка задачи управления позволяет искать решение для управляющего воздействия . Такая постановка задачи управления позволяет искать решение для управляющего воздействия  в форме функции вектора в форме функции вектора  (модальное управление). Регулятор представляется в виде функционального преобразователя составляющих вектора (модальное управление). Регулятор представляется в виде функционального преобразователя составляющих вектора  . Наиболее известным методом определения такого регулятора является метод АКОР (аналитическое конструирование оптимальных регуляторов), позволяющий определять функциональную форму управления . Наиболее известным методом определения такого регулятора является метод АКОР (аналитическое конструирование оптимальных регуляторов), позволяющий определять функциональную форму управления  на основе решения задачи оптимизации критерия на основе решения задачи оптимизации критерия  . Основным недостатком оптимального регулятора является необходимость иметь информацию о всех переменных состояния ОК для определения управляющего воздействия . Основным недостатком оптимального регулятора является необходимость иметь информацию о всех переменных состояния ОК для определения управляющего воздействия  . В рассматриваемой АдСУ оптимальный регулятор заменяется нечетким регулятором (НР). Согласно теоретическим доказательствам [21] НР аппроксимирует любую непрерывную функцию с заданной точностью. Это его свойство позволяет использовать НР в качестве аппроксиматора оптимального регулятора. Кроме того НР может работать на основе сигнала ошибки основного контура, что очень важно для практической реализации АдСУ. Пусть объект управления имеет математическое описание: . В рассматриваемой АдСУ оптимальный регулятор заменяется нечетким регулятором (НР). Согласно теоретическим доказательствам [21] НР аппроксимирует любую непрерывную функцию с заданной точностью. Это его свойство позволяет использовать НР в качестве аппроксиматора оптимального регулятора. Кроме того НР может работать на основе сигнала ошибки основного контура, что очень важно для практической реализации АдСУ. Пусть объект управления имеет математическое описание:
  … …  (2.25) (2.25)
Для определения оптимального управления (ОпРег) по методу  принимаем критерий оптимизации в форме принимаем критерий оптимизации в форме
 (2.26) (2.26)
Где  – макропеременная, представляющая собой некоторую произвольную дифференцируемую или кусочно-дифференцируемую функцию фазовых координат – макропеременная, представляющая собой некоторую произвольную дифференцируемую или кусочно-дифференцируемую функцию фазовых координат  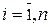 , ,  . Согласно [22] оптимальное управление . Согласно [22] оптимальное управление  можно получить в результате решения уравнения можно получить в результате решения уравнения
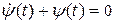
Для ОУ с описанием (2.25) оптимальное управление имеет вид:
 (2.27) (2.27)
Работа нечеткого регулятора основана на понятиях нечеткого множества, лингвистической переменной и нечеткой логики. При использовании НР в детерминированных САУ входные переменные регулятора проходят операцию фаззификации, где они представляются множеством лингвистических значений (например, ошибка: маленькая, средняя, большая) или термов  , где i – индекс лингвистической переменной и j - индекс множества лингвистических значений, каждое из которых характеризуется нечетким подмножеством , где i – индекс лингвистической переменной и j - индекс множества лингвистических значений, каждое из которых характеризуется нечетким подмножеством  . Нечеткое подмножество содержит элементы базового множества X с частичной принадлежностью этому множеству, характеризуемый числом из интервала . Нечеткое подмножество содержит элементы базового множества X с частичной принадлежностью этому множеству, характеризуемый числом из интервала  и определяемой функцией принадлежности и определяемой функцией принадлежности   . Ядром НР является механизм принятия решения об управлении на базе набора условных операторов, называемых продукционными правилами, сформулированными в терминах лингвистических переменных, заданных термами. Например: . Ядром НР является механизм принятия решения об управлении на базе набора условных операторов, называемых продукционными правилами, сформулированными в терминах лингвистических переменных, заданных термами. Например:
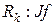  is is  AND … AND AND … AND  is is  THEN U is THEN U is 
где U – выходная переменная,  – терм выходной переменной. – терм выходной переменной.
На первом этапе работы нечеткого регулятора (операция фаззификации) для текущего момента времени t и каждой входной переменной  происходит расчет значений функций принадлежности по значению происходит расчет значений функций принадлежности по значению  . Затем определяется степень истинности . Затем определяется степень истинности  каждого продукционного правила на основании правил нечеткой логики. Для выходных переменных НР также задаются функции принадлежности термов. Функция принадлежности нечеткого подмножества лингвистической переменной выходного (управляющего) сигнала формируется в результате применения процедуры импликации к совокупности степени истинности правил и функциям принадлежности термов выходной переменной. В результате получается функция принадлежности выходной переменной каждого продукционного правила на основании правил нечеткой логики. Для выходных переменных НР также задаются функции принадлежности термов. Функция принадлежности нечеткого подмножества лингвистической переменной выходного (управляющего) сигнала формируется в результате применения процедуры импликации к совокупности степени истинности правил и функциям принадлежности термов выходной переменной. В результате получается функция принадлежности выходной переменной  . Завершающий этап работы НР – дефаззификация. На основании этой процедуры происходит преобразование значений лингвистических переменных выходного сигнала в виде нечеткого подмножества с функцией принадлежности . Завершающий этап работы НР – дефаззификация. На основании этой процедуры происходит преобразование значений лингвистических переменных выходного сигнала в виде нечеткого подмножества с функцией принадлежности  в численное значение сигнала u. Необходимая особенность НР принятого в АдСУ состоит в особой форме функций принадлежности термов выходного сигнала, которые задаются в виде в численное значение сигнала u. Необходимая особенность НР принятого в АдСУ состоит в особой форме функций принадлежности термов выходного сигнала, которые задаются в виде 
где  , j=1…L - коэффициенты настройки регулятора, представляющие собой дискретные значения, которые может принимать управляющий сигнал. Эта форма , j=1…L - коэффициенты настройки регулятора, представляющие собой дискретные значения, которые может принимать управляющий сигнал. Эта форма  позволяет представить в дальнейшем сигнал и в аналитической форме. позволяет представить в дальнейшем сигнал и в аналитической форме.
В результате применения метода центральной площади для решения задачи дефаззификации численное значение управляющего сигнала при входных сигналах  принимает вид [20]: принимает вид [20]:
 (2.28) (2.28)
Выражение (2.28) будет реализуемым, если знаменатель (2.28) не обращается в ноль. Поэтому целесообразно выбирать функции принадлежности термов входного сигнала в виде:
 где где 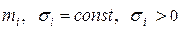
Если обозначить  - оптимальное управление, тогда - оптимальное управление, тогда  , где , где  – вектор настройки коэффициентов нечеткого регулятора, точно воспроизводящий оптимальный закон управления. При этом значения составляющих – вектор настройки коэффициентов нечеткого регулятора, точно воспроизводящий оптимальный закон управления. При этом значения составляющих  еще требуется определить. В рассматриваемой АдСУ эта задача решается при рассмотрении вопроса обеспечения устойчивости системы в целом. Устойчивая работа любой системы автоматического управления, как правило, связана с ограничениями на некоторые параметры, которые подбираются именно так, чтобы САУ обладала устойчивостью. Такими параметрами могут быть составляющие еще требуется определить. В рассматриваемой АдСУ эта задача решается при рассмотрении вопроса обеспечения устойчивости системы в целом. Устойчивая работа любой системы автоматического управления, как правило, связана с ограничениями на некоторые параметры, которые подбираются именно так, чтобы САУ обладала устойчивостью. Такими параметрами могут быть составляющие  . В качестве критерия устойчивости принимается второй метод Ляпунова. При формировании функции Ляпунова V в ее состав вводится слагаемое, содержащее искомые составляющие . В качестве критерия устойчивости принимается второй метод Ляпунова. При формировании функции Ляпунова V в ее состав вводится слагаемое, содержащее искомые составляющие  : :  , где , где  ; γ – положительный коэффициент. Полная производная функции Ляпунова имеет вид ; γ – положительный коэффициент. Полная производная функции Ляпунова имеет вид
 , где , где 
При определении значений  следует учитывать описание объектом (8.1). Для этого система уравнений для объекта (2.25) представляется в виде: следует учитывать описание объектом (8.1). Для этого система уравнений для объекта (2.25) представляется в виде:


.....
 (2.29) (2.29)
С учетом аппроксимации управляющего воздействия  нечетким регулятором нечетким регулятором  и и  и оптимального управления и оптимального управления  (2.27) система (2.29) принимает форму: (2.27) система (2.29) принимает форму:


.....
 (2.30) (2.30)
При описании объекта управления (2.30) полная производная по времени от функции Ляпунова равна:

Отметим, что  . Тогда . Тогда  примет вид: примет вид:
 (2.31) (2.31)
Согласно методу Ляпунова условием устойчивости замкнутой системы является отрицательное значение производной  . Согласно (2.31) это условие будет выполнено, если определять значение . Согласно (2.31) это условие будет выполнено, если определять значение  из уравнения из уравнения

Для решения практических задач удобно принять функцию  , где e - ошибка основного контура системы e = yзад - , где e - ошибка основного контура системы e = yзад -  . При описании ОУ обычно принимают . При описании ОУ обычно принимают  , тогда e = yзад - , тогда e = yзад -  , ,  . Тогда . Тогда  . Переменная . Переменная  согласно (2.25) входит в уравнение, которое содержит управляющее воздействие u, тогда в этом случае согласно (2.25) входит в уравнение, которое содержит управляющее воздействие u, тогда в этом случае  . .
В качестве примера рассмотрим определение закона адаптации для объекта, структурная схема которого показана на рис. 2.7

Рис 2.7
Математическое описание этого объекта в переменных состояния имеет вид:



Функциональная блок-схема АдСУ имеет вид рис (2.6). Выходная переменная НР является управляющим воздействием  . Макропеременная . Макропеременная  Ошибка основного контура при g(t)- yзад e = yзад - Ошибка основного контура при g(t)- yзад e = yзад - 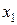 , , 
Уравнение адаптации:

В том случае, когда функция 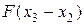 принимает постоянное значение или равна нулю (частная производная по x равна нулю) процесс адаптации не происходит. Если принимает постоянное значение или равна нулю (частная производная по x равна нулю) процесс адаптации не происходит. Если 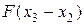 – статическое нелинейное звено и производная – статическое нелинейное звено и производная 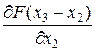 =const, сигнал управления в НР формируется согласно уравнению =const, сигнал управления в НР формируется согласно уравнению

|




 изменяются синхронно (с некоторой инерционностью) с изменением параметров ОУ. Необходимое значение составляющих
изменяются синхронно (с некоторой инерционностью) с изменением параметров ОУ. Необходимое значение составляющих  и ее производной
и ее производной  в основном контуре управления. Блок АА содержит процедуру дифференцирования
в основном контуре управления. Блок АА содержит процедуру дифференцирования  относительно переменных состояния объекта вектора
относительно переменных состояния объекта вектора 
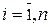 . Такая постановка задачи управления позволяет искать решение для управляющего воздействия
. Такая постановка задачи управления позволяет искать решение для управляющего воздействия  в форме функции вектора
в форме функции вектора  (модальное управление). Регулятор представляется в виде функционального преобразователя составляющих вектора
(модальное управление). Регулятор представляется в виде функционального преобразователя составляющих вектора  на основе решения задачи оптимизации критерия
на основе решения задачи оптимизации критерия  . В рассматриваемой АдСУ оптимальный регулятор заменяется нечетким регулятором (НР). Согласно теоретическим доказательствам [21] НР аппроксимирует любую непрерывную функцию с заданной точностью. Это его свойство позволяет использовать НР в качестве аппроксиматора оптимального регулятора. Кроме того НР может работать на основе сигнала ошибки основного контура, что очень важно для практической реализации АдСУ. Пусть объект управления имеет математическое описание:
. В рассматриваемой АдСУ оптимальный регулятор заменяется нечетким регулятором (НР). Согласно теоретическим доказательствам [21] НР аппроксимирует любую непрерывную функцию с заданной точностью. Это его свойство позволяет использовать НР в качестве аппроксиматора оптимального регулятора. Кроме того НР может работать на основе сигнала ошибки основного контура, что очень важно для практической реализации АдСУ. Пусть объект управления имеет математическое описание:
 …
…  (2.25)
(2.25) принимаем критерий оптимизации в форме
принимаем критерий оптимизации в форме (2.26)
(2.26) – макропеременная, представляющая собой некоторую произвольную дифференцируемую или кусочно-дифференцируемую функцию фазовых координат
– макропеременная, представляющая собой некоторую произвольную дифференцируемую или кусочно-дифференцируемую функцию фазовых координат 
 . Согласно [22] оптимальное управление
. Согласно [22] оптимальное управление  можно получить в результате решения уравнения
можно получить в результате решения уравнения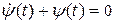
 (2.27)
(2.27) , где i – индекс лингвистической переменной и j - индекс множества лингвистических значений, каждое из которых характеризуется нечетким подмножеством
, где i – индекс лингвистической переменной и j - индекс множества лингвистических значений, каждое из которых характеризуется нечетким подмножеством  . Нечеткое подмножество содержит элементы базового множества X с частичной принадлежностью этому множеству, характеризуемый числом из интервала
. Нечеткое подмножество содержит элементы базового множества X с частичной принадлежностью этому множеству, характеризуемый числом из интервала  и определяемой функцией принадлежности
и определяемой функцией принадлежности 
 . Ядром НР является механизм принятия решения об управлении на базе набора условных операторов, называемых продукционными правилами, сформулированными в терминах лингвистических переменных, заданных термами. Например:
. Ядром НР является механизм принятия решения об управлении на базе набора условных операторов, называемых продукционными правилами, сформулированными в терминах лингвистических переменных, заданных термами. Например: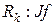
 is
is  AND … AND
AND … AND  is
is  THEN U is
THEN U is 
 происходит расчет значений функций принадлежности по значению
происходит расчет значений функций принадлежности по значению  . Затем определяется степень истинности
. Затем определяется степень истинности  каждого продукционного правила на основании правил нечеткой логики. Для выходных переменных НР также задаются функции принадлежности термов. Функция принадлежности нечеткого подмножества лингвистической переменной выходного (управляющего) сигнала формируется в результате применения процедуры импликации к совокупности степени истинности правил и функциям принадлежности термов выходной переменной. В результате получается функция принадлежности выходной переменной
каждого продукционного правила на основании правил нечеткой логики. Для выходных переменных НР также задаются функции принадлежности термов. Функция принадлежности нечеткого подмножества лингвистической переменной выходного (управляющего) сигнала формируется в результате применения процедуры импликации к совокупности степени истинности правил и функциям принадлежности термов выходной переменной. В результате получается функция принадлежности выходной переменной  . Завершающий этап работы НР – дефаззификация. На основании этой процедуры происходит преобразование значений лингвистических переменных выходного сигнала в виде нечеткого подмножества с функцией принадлежности
. Завершающий этап работы НР – дефаззификация. На основании этой процедуры происходит преобразование значений лингвистических переменных выходного сигнала в виде нечеткого подмножества с функцией принадлежности 
 , j=1…L - коэффициенты настройки регулятора, представляющие собой дискретные значения, которые может принимать управляющий сигнал. Эта форма
, j=1…L - коэффициенты настройки регулятора, представляющие собой дискретные значения, которые может принимать управляющий сигнал. Эта форма  позволяет представить в дальнейшем сигнал и в аналитической форме.
позволяет представить в дальнейшем сигнал и в аналитической форме. принимает вид [20]:
принимает вид [20]: (2.28)
(2.28) где
где 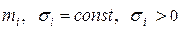
 , где
, где  – вектор настройки коэффициентов нечеткого регулятора, точно воспроизводящий оптимальный закон управления. При этом значения составляющих
– вектор настройки коэффициентов нечеткого регулятора, точно воспроизводящий оптимальный закон управления. При этом значения составляющих  , где
, где  ; γ – положительный коэффициент. Полная производная функции Ляпунова имеет вид
; γ – положительный коэффициент. Полная производная функции Ляпунова имеет вид , где
, где 


 (2.29)
(2.29) нечетким регулятором
нечетким регулятором  и
и  и оптимального управления
и оптимального управления  (2.27) система (2.29) принимает форму:
(2.27) система (2.29) принимает форму: (2.30)
(2.30)
 . Тогда
. Тогда  примет вид:
примет вид: (2.31)
(2.31) . Согласно (2.31) это условие будет выполнено, если определять значение
. Согласно (2.31) это условие будет выполнено, если определять значение 
 , где e - ошибка основного контура системы e = yзад -
, где e - ошибка основного контура системы e = yзад -  . При описании ОУ обычно принимают
. При описании ОУ обычно принимают  , тогда e = yзад -
, тогда e = yзад -  ,
,  . Тогда
. Тогда  . Переменная
. Переменная  .
.



 . Макропеременная
. Макропеременная  Ошибка основного контура при g(t)- yзад e = yзад -
Ошибка основного контура при g(t)- yзад e = yзад - 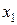 ,
, 

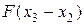 принимает постоянное значение или равна нулю (частная производная по x равна нулю) процесс адаптации не происходит. Если
принимает постоянное значение или равна нулю (частная производная по x равна нулю) процесс адаптации не происходит. Если 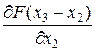 =const, сигнал управления в НР формируется согласно уравнению
=const, сигнал управления в НР формируется согласно уравнению



