
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы поиска экстремумов унимодальных функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пользуясь тем же приемом, но вычисляя значение функции в подинтервалах неодинаковое число раз, можно дополнительно повысить эффективность поиска. Вычисляя N значений функций на i последовательно сужаемых интервалах, получим для коэффициента дробления интервала неопределенности
При таком методе поиска целевую функцию приходится вычислять J раз, причем J = Ni. Можно найти оптимальное значение N, при котором J при заданном f д минимально. Зная что i = J/N можно получить
Такая функция имеет минимум при N =3. При этом на каждом интервале f д=0.5, т.е. каждые три измерения позволяют сузить интервалы неопределенности вдвое. Поскольку интервал неопределенности делится каждый раз надвое, то метод получил название метода деления интервала пополам. На рис.4.6 показано, что три первых вычисленных значения функции позволяют сузить интервал неопределенности вдвое.
Рис. 4.6 Заметим далее, что значение целевой функции в середине нового интервала уже известно. Поэтому для завершения поиска на следующем этапе потребуется вычислить только два (вместо трех) значений целевой функции. В общем случае при N ³3 коэффициент дробления интервала неопределенности составит
Выше предполагалось, что значения целевой функции вычисляются при постоянном приращении проектного параметра. Если снять это ограничение, то эффективность поиска можно повысить. Как уже отмечалось, вычисление целевой функции в двух точках интервала неопределенности позволяет его сузить. Можно таким образом выбрать эти точки, что интервал неопределенности будет минимальным. На рис. 4.7 показаны обозначения, используемые в этой схеме. Если значение целевой функции в x 1 больше, чем в х 2, т.е. f (x 1) > f (x 2), то новый интервал неопределенности z `= z 1 + z 2. Если f (x 1) < f (x 2), то z `` = z 2 + z 3. Задача состоит в том, чтобы одновременно минимизировать z ` и z ``, удовлетворив условиям
z 1 > 0; z 2 > 0; z 3 > 0.
Рис. 4.7 Из равенства (4.1) можно исключить z 2. Тогда z-z 3= min и z-z 1= min. Так как величина z задана, то правые части уравнений будут тем меньше, чем одновременно большими будут z 1 и z 3. Следовательно, оптимум соответствует условию z 1= z 3= z /2. Но тогда из (4.1) видно, что z 2=0, что противоречит условию z 2>0. Пусть z 2 имеет очень малое значение e. Тогда из z 1 и z 3 вычтем по e/2. В результате после вычислений первой пары значений целевой функции при близких значениях x 1 и x 2 интервал неопределенности сузится, как показано на рис. 4.8, и коэффициент дробления на шаге будет равен
Рис. 4.8 Очевидно в пределе, при e®0, f д ®1/2. В дальнейшем, при использовании метода дихотомии выполняются те же операции, что и при методе деления интервала пополам. Отметим, однако, что для достижения одинаковых сужений интервала неопределенности метод дихотомии требует вычисления целевой функции в точках на одну меньше. Рассмотрим метод золотого сечения. Сущность метода состоит в следующем. Интервал неопределенности делится на две части так, чтобы отношение длины большего отрезка к длине всего интервала было бы равно отношению длины меньшего отрезка к большему. На рис. 4.9 показан интервал неопределенности z, состоящий из отрезков z 1 и z 2, отношение длин которых определяется правилом золотого сечения
Рис. 4.9
Из (4.2) следует z 12 = z 2 z. Подставим z из (4.3) z = z 2 + z 1 и получим z 12= z 22 + z 1 z 2. Разделим обе части на z 12
Решая это квадратное уравнение, находим для положительного корня значение
На рис. 4.10 показано деление интервала неопределенности в этом соотношении и нанесены соответствующие значения целевой функции, которые позволяют уменьшить интервал неопределенности в 1/0.618 раза.
Рис. 4.10 На этой стадии еще не видны преимущества метода золотого сечения перед методом дихотомии, однако они явно проявляются при дальнейшем делении интервала, так как оказывается, что одно из значений целевой функции, которое требуется вычислить на следующем шаге уже известно. Поэтому, чтобы уменьшить неопределенность еще в 1/0.618 раза потребуется дополнительно только одно значение целевой функции в новой точке. После вычисления N значений целевой функции коэффициент дробления интервала неопределенности составляет N -1 f д = 0,618, где (N -1) - число шагов.
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 741; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.82.60 (0.006 с.) |


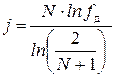 .
.













