
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Антагонистически матричные игры и их решениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Самым простым случаем в теории игр является конечная парная игра с нулевой суммой (антагонистическая игра двух лиц или двух коалиций). Рассмотрим такую игру G, в которой участвуют 2 игрока А и B, имеющие противоположные интересы: выигрыш одного равен проигрышу другого. Если это так, то мы можем интересоваться только выигрышем игрока А. Естественно, А хочет максимизировать свой выигрыш, а В хочет его минимизировать, так как это его проигрыш. Пусть у игрока А имеется m возможных стратегий Ai i =1, m, а у игрока B - n возможных стратегий Bj j =1, n Обозначим выигрыш игрока А через aij, что означает, что A воспользовался стратегией Ai, а B стратегией Bj. Предположим, что для каждой пары стратегий Ai, Bj выигрыш aij нам известен. Тогда можно составить прямоугольную матрицу, в которой перечислены стратегии игроков и соответствующие выигрыши. Такая матрица еще называется платежной матрицей. Таблица 6.1
Если такие таблицы составлены, то говорят, что игра G приведена к матричной форме. Кстати, само по себе приведение игры к матричной форме может представлять трудную задачу из-за необозримого множества стратегий и неясностей в выигрышах. Заметим, что если игра приведена к матричной форме, то многоходовая игра фактически сведена к одноходовой. От игрока требуется сделать только один ход - выбрать стратегию. Рассмотрим пример игры G (4х5) в матричной форме. У игрока A четыре стратегии, у игрока B - 5. Таблица 6.2
Поразмышляем какой стратегией игроку A воспользоваться? Неплохо бы на первый взгляд воспользоваться стратегией A 3 и получить выигрыш 10. Но это будет лишь в том случае, если B воспользуется B 1. Если же B выберет B 3, то A получит всего лишь 1. Как же быть? Очевидно, из принципа гарантированного результата (а в теории игр это основной принцип, его иначе называют принцип минимакса) надо выбрать ту стратегию, при которой минимальный выигрыш A максимален. Сделаем в матрице дополнительный правый столбец, куда и запишем минимальные выигрыши A при каждой из его стратегий. Выделим наибольшее значение - 3. Эта величина - гарантированный выигрыш Ai; ведя себя осторожно меньше этого мы не выиграем (а может быть и больше). Этот выигрыш называется нижней ценой игры или max min (максимальный из минимальных выигрышей). Обозначим его a = 3
Теперь порассуждаем за игрока B. Играя, он хотел бы отдать поменьше, но должен рассчитывать на наихудшее поведение A. Припишем к таблице нижнюю строку, куда впишем max проигрыши B и выделим минимальный из максимальных проигрышей. Он равен 5. Это min max или верхняя цена игры. Обозначим его b. Это тот проигрыш, больше которого умный противник нам не отдаст. Возвращаясь к первой таблице запишем принцип минимакса: анализируя наши стратегии Аi выбираем в каждой из строк минимальный выигрыш aij и обозначаем его
Строим дополнительный столбец и сводим в него все значения a i. Из этого столбца выбираем максимальное значение a i обозначим его a = max a i. Учитывая (6.1) запишем
Величина a называется нижней ценой игры или максимином. Для игрока В: в столбцах выбираем максимальные значения выигрышей aij и обозначаем b i = max aij. Строим дополнительную строку снизу и сводим в нее значения b i, из них выбираем минимальное
Величина b называется верхней ценой игры или максимином. Этот принцип вытекает из предположения о разумности игроков, стремящихся достигнуть цели, противоположной цели противника. Итак, исходя из принципа осторожности A выбирает стратегию A 4, а B - стратегию B 3. Устойчивы ли эти стратегии по отношению к информации о поведении противника. В нашем примере - нет. Допустим, игрок A узнал, что B придерживается B 3. Он тут же воспользуется A 1 и получит выигрыш равный 5. Но B в ответ ему выберет B 4, сводя выигрыш к 2 и т.д. Рассмотрим другую игру. В этом примере нижняя цена игры равна верхней a = b = 6. Что из этого следует. Минимаксные стратегии игроков A и B будут устойчивыми. Пока оба игрока их придерживаются выигрыш будет равен 6. Допустим A узнал, что B придерживается B 2. Выберет ли он другую стратегию? Нет. В свою очередь B узнав, что A придерживается стратегии A 2 не изменит своей, так как проиграет еще больше. Таблица 6.3
Пара стратегий A 2, B 2 обладает свойством равновесия, а выигрыш называется седловой точкой матрицы. Признак наличия седловой точки - это равенство нижней и верхней цены игры. При этом общее значение a и b называется ценой игры. Стратегии в этом случае называются оптимальными чистыми стратегиями, а их совокупность - решением игры. Наличие седловой точки в игре - это далеко не правило. И тем не менее есть игры, которые всегда имеют седловую точку и решаются в чистых стратегиях. Это так называемые игры с полной информацией. Игрой с полной информацией называется такая игра, в которой игрок при каждом личном ходе знает всю предысторию игры: шашки, шахматы и т.п. В каждой такой игре существует пара стратегий, дающая устойчивый выигрыш, равный цене игры. Элементарный пример: игроки кладут пятаки на стол. Проигрывает тот, кто не может положить очередной пятак на стол. Легко показать, что выигрывает тот, кто начинает. Для этого ему нужно первый пятак положить в центр стола, а затем на каждый ход противника отвечать симметричным ходом. Шахматная партия всегда заканчивается либо победой белых, либо -победой черных, либо ничьей, только чем именно мы не знаем, да и вряд ли будем знать в обозримом будущем. При многократном повторении игры игрок может с определенной вероятностью смешивать свои стратегии. Доказано, что в смешанных стратегиях каждая конечная игра имеет седловую точку. Упрощение игр. Если игра m x n не имеет седловой точки, то отыскание ее решения, особенно при больших m и n, представляет собой довольно трудоемкую задачу. Иногда эту задачу удается сузить, если предварительно упростить игру, т.е. сократить число стратегий путем вычеркивания некоторых излишних. Излишние стратегии бывают двух родов: дублирующие и заведомо невыгодные. Рассмотрим, например игрус матрицей: Таблица 6.4
Из матрицы видно, что стратегия А 3 в точности дублирует стратегию А 1; поэтому любую из этих двух стратегий можно вычеркнуть. Далее, сравнивая почленно строки А 1 и А 2, видим, что все элементы строки А 2 меньше (или равны) соответствующих элементов строки А 1. Значит, стратегия А 2 для нас не выгодна. Вычеркивая А 3 и А 2, приведем матрицу к более простому виду: Таблица 6.5
Для противника В стратегия В 3 заведомо невыгодна; вычеркиваем и ее, матрица приводится к виду, а игра 4х4 сведена к игре 2х3.
Таблица 6.6
Иногда удается упростить игру искусственным введением вместо чистых стратегий - смешанных. Пусть имеется игра 3х4 с матрицей: Таблица 6.7
Рассматривая матрицу, замечаем, что, в силу симметрии элементов столбцов В 1 и В 2; В 3 и В 4, а также строк А 1 и А 2, эти стратегии, если входят в решение, то только с одинаковыми вероятностями: p 1= p 2, q 1= q 2, q 3= q 4. Отсюда возникает идея: заранее объединить стратегии В 1 и В 2 в одну смешанную стратегию В 12, состоящую наполовину из В 1, наполовину из В 2. Также поступаем со стратегиями В 3 и В 4. Матрица приводится к виду:
Таблица 6.8
Теперь видно, что если противник пользуется стратегиями В 12, В 34, стратегии А 1 и А 2 дублируют друг друга; вычеркивая какую-либо из них (или объединяя А 1 и А 2 в одну А 12), приводим матрицу к виду 2х2: Таблица 6.9
Таким образом, игра 3х4 сведена к игре 2х2. Приступая к решению любой игры m x n, необходимо прежде всего выполнить следующие процедуры: - посмотреть, нет ли в матрице седловой точки: если есть, решение уже найдено; - если седловой точки нет, сравнить между собой почленно столбцы и строки с целью вычеркивания дублирующих и заведомо невыгодных стратегий; - посмотреть, нельзя ли уменьшить число стратегий путем замены некоторых групп чистых - смешанными. 6.2.2. Графический метод решения игр 2х n и m х2 Рассмотрим игру 2х2 Таблица 6.10
Возьмем участок оси абсцисс длиной единица (см. рис.6.3) Левый конец участка (точка с абсциссой х =0) будет изображать стратегию А 1, правый конец участка (х =1) - стратегию А 2; все промежуточные точки участка будут изображать смешанные стратегии игрока А, причем вероятность р1 стратегии А 1 будет равна расстоянию от точки SA до правого конца участка, а вероятность р 2 - расстоянию от точки до левого конца. Проведем через точки А 1 и А 2 два перпендикуляра к оси абсцисс: ось I-I и ось II-II. На оси I-I будем откладывать выигрыш при стратегии А 1, на оси I I-I I - выигрыши при стратегии А 2.
Рис.6.3
Пусть противник применяет стратегию В 1; она дает на осях I-I и II-II соответственно точки с ординатами а 11 и а 21. Проведем через эти точки прямую В 1 В 1. Эта прямая отображает наш выигрыш при любой смешанной стратегии; например точка М - выигрыш при стратегии SA = (p 1, p 2). Прямую В 1 В 1 условно назовем «стратегией В 1» таким же способом строится стратегия В 2. При решении игры необходимо найти оптимальную стратегию SA*, т.е. такую при которой наш минимальный выигрыш (при наихудшем для нас поведении В) обращался бы в максимум. Для этого строим нижнюю границу выигрыша при стратегиях В 1, В 2 - это ломаная B 1 NB 2. На этой границе будет лежать минимальный выигрыш игрока А при любой смешанной стратегии; точка N определяет решение и цену игры. Рассмотрим какие возможны случаи при решении игр графическим методом. На рис. 6.4 показан случай, когда оптимальной стратегией игрока А является чистая стратегия А 2, хотя это и не соответствует точке пересечения стратегий. На рис. 6.5 изображен случай, когда заведомо невыгодная стратегия В 2 имеется у противника.
Рис. 6.4.
Рис. 6.5.
Для игр с большим числом стратегий чем 2 расмотрим игру 2х n. Матрица ее имеет вид Таблица 6.11
a ¹ b Седловой точки нет, решения в чистых стратегиях нет. Найдем графическим методом смешанные стратегии.
Рис. 6.6.
С вероятностью P 1 A применяет 1-ю стратегию и с вероятностью P 2 - вторую.
Методы решения конечных игр До сих пор мы рассматривали только элементарные игры 2х n, m х2 для которых существует простая геометрическая интерпретация, позволяющая решать эти игры с помощью простейших приемов. В случае игр 3х n или m х3 подобная интерпретация также может быть построена, но вместо плоской она становится пространственной и гораздо менее наглядной. В случае игры m х n при m,n >3 от геометрической интерпретации приходится отказаться и в силу вступают чисто расчетные методы решения игр. В общем случае, при больших m и n, решение игры представляет собой довольно трудоемкую задачу, но принципиальных трудностей не содержит. Можно легко показать, что решение любой конечной игры m х n может быть сведено к известной нам задаче линейного программирования. 6.3.1. Решение игр m x n Пусть имеется игра m х n без седловой точки с матрицей aij , то есть a¹b. Допустим, что все выигрыши aij положительны. Если это не так, то этого всегда можно добиться, прибавляя ко всем членам матрицы достаточно большое число M; от этого цена игры увеличится на M, а решение SA* , SB* не изменится. Если все aij положительны, то и цена игры, то есть средний выигрыш при оптимальной стратегии, тоже положителен: V >0. Таблица 6.12
Мы хотим найти решение игры, то есть две оптимальные смешанные стратегии, дающие каждой стороне максимально возможный для нее средний выигрыш (или минимальный средний проигрыш)
где р 1+ р 2+...+ рm =1; q 1+ q 2+...+ qn =1 - вероятности применения чистых стратегий и оптимальный средний выигрыш. Найдем оптимальную стратегию игрока A, то есть SA*. Мы уже знаем, что если один из игроков (в данном случае А) применяет свою оптимальную стратегию, то другой игрок не может улучшить свое положение, отступая от своей оптимальной стратегии. Заставим все же игрока В отступать от своей оптимальной стратегии, пользуясь при этом чистыми стратегиями B 1, B 2,... Bn. Сам же игрок A по-прежнему придерживается своей оптимальной стратегии SA*. При этом выигрыш игрока A при любой чистой стратегии Bi будет не меньше цены игры V. Опишем это.
Первое неравенство говорит о том, что игрок A применяет свои стратегии Ai (i =1, m) с вероятностями pi (i = 1, m), при этом игрок B применяет свою первую чистую стратегию. Разделим левые и правые части неравенства на положительную величину V и введем обозначения
Тогда условия (6.6) примут вид
где x 1, x 2,..., xm - как видно из (6.6) неотрицательные числа. P 1 + P 2 + P 3+... Pm = 1 и в силу (6.6) переменные
Но, что такое V. Это гарантированный выигрыш игрока A. Очевидно, что A хочет свой гарантированный выигрыш максимизировать, а это значит, что величина 1/ V будет стремиться к min. Таким образом, задача решения игры свелась к математической задаче: найти неотрицательные значения переменных x 1, x 2,..., xm такие, чтобы они удовлетворяли линейным ограничениям - неравенствам (6.7) и обращали в минимум линейную функцию этих переменных:
Что за запись мы видим перед собой? Очевидно, это запись задачи линейного программирования. Таким образом, задача решения игры m х n свелась к задаче ЛП с n ограничениями неравенствами и m переменными. Найдя переменные x 1, x 2,..., xm например, (симплекс-методом) можно по формулам (6.8) и (6.6) найти сначала V, затем p 1, p 2,..., pm, а значит найти цену игры и оптимальную стратегию SA *. Оптимальная стратегия игрока B находится совершенно аналогично, с одной лишь разницей. B стремится минимизировать выигрыш, а значит и цену игры V или, что то же самое, максимизировать величину 1/ V. Кроме того, в ограничениях - неравенствах знаки будут обратные. Напишем задачу ЛП для игрока B
Пара задач линейного программирования (6.7), (6.9) и (6.10), (6.11) по которой находятся оптимальные стратегии SA* и SB* называется парой двойственных задач линейного программирования. Доказано, что максимум линейной функции в одной из них, равен минимуму в другой, а это значит, что цена игры V будет одинаковой в обеих задачах, а это в свою очередь значит, что a=b и седловая точка достигнута. Таким образом, решение игры m x n эквивалентно решению задачи линейного программирования. Нужно заметить, что и наоборот, - для любой задачи ЛП может быть построена эквивалентная ей задача теории игр. Эта связь оказывается очень полезной. Дело в том, что существуют приближенные численные методы решения игр, которые при большой размерности задач ЛП оказываются проще, чем «классические» методы ЛП. Пример: найти методом ЛП решение игры, заданной матрицей Таблица 6.13
Прибавим к элементам матрицы М =5, сделаем их неотрицательными. Стратегия А 4 по сравнению с А 1 заведомо невыгодная, поэтому ее исключаем. Находим верхнюю и нижнюю цену игры: a=2; b=9; a¹b, седловой точки нет n = g+5.
Найдем оптимальную смешанную стратегию игрока А SA =(p 1, p 2, p 3). Условия (6.7) примут вид:
Минимизируемая линейная функция
Перейдем от условий неравенств (6.12) к условиям равенств
Результат: Lmin = 1/5 при y 1= y 2= y 3=0, x 1=1/20; x 2=1/10; x 3=1/20 Тогда n = 1/ Lmin =5, a g = n-5 = 0. Это значение выигрыша достигается при вероятностях стратегий: p 1=1/4; p 2=1/2; p 3=1/4, т.е. SA =(0,25; 0,5; 0,25)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 748; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.149.244 (0.01 с.) |


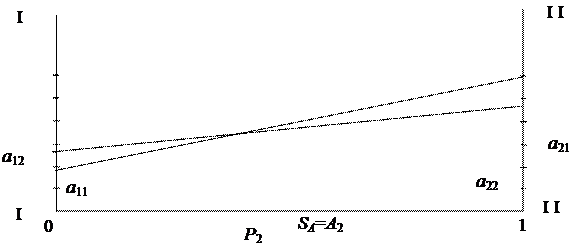

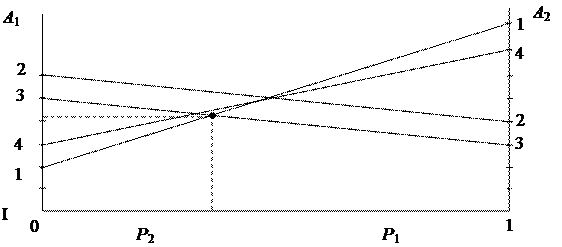
 a 12 p 1+ a 22 p 2+...+ a 32 p 3 +...+ am 2 pm ³ V
………………………………………
a 1 n p 1+ a 2n p 2+...+ a 3 n p 3 +...+ amnpm ³ V
a 12 p 1+ a 22 p 2+...+ a 32 p 3 +...+ am 2 pm ³ V
………………………………………
a 1 n p 1+ a 2n p 2+...+ a 3 n p 3 +...+ amnpm ³ V




