
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка транспортной задачи линейного программированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Симплекс-метод решения задачи линейного программирования является универсальным и применим для решения любых таких задач. Однако существуют некоторые частные типы задач линейного программирования, которые, в силу некоторых особенностей своей структуры, допускают решение более простыми методами. К ним относится, в частности, так называемая транспортная задача. Классическая транспортная задача линейного программирования формулируется следующим образом. Имеется m пунктов отправления: А 1, А 2,..., Am, в которых сосредоточены запасы какого-то однородного товара (груза) в количестве соответственно a 1, a 2,..., am единиц. Кроме того, имеется n пунктов назначения: B 1, B 2,..., Bn, подавших заявки соответственно на b 1, b 2,..., bn единиц товара. Предполагается, что сумма всех заявок равна сумме всех запасов:
Известна стоимость cij перевозки единицы товара от каждого пункта отправления Ai до каждого пункта назначения Bj. Таблица (матрица) стоимостей перевозки сij задана:
Требуется составить такой план перевозок, при котором все заявки были бы выполнены, и при этом общая стоимость всех перевозок была минимальна. При такой постановке задачи показателем эффективности плана перевозок является стоимость; поэтому поставленную задачу точнее называют транспортной задачей по критерию стоимости. Дадим этой задаче математическую формулировку. Обозначим xij - количество груза, отправляемого из i -го пункта отправления Аi в j -й пункт назначения Вj (i = 1,..., m; j = 1,..., n). Неотрицательные переменные x 11, x 12,..., xmn (число которых, очевидно, равно m x n) должны удовлетворять следующим условиям: 1. Суммарное количество груза, направляемое из каждого пункта отправления во все пункты назначения, должно быть равно запасу груза в данном пункте. Это даст нам m условий-равенств:
или, короче,
2. Суммарное количество груза, доставляемое в каждый пункт назначения изо всех пунктов отправления, должно быть равно заявке, поданной данным пунктом. Это даст n условий-равенств:
или, короче,
3. Суммарная стоимость всех перевозок, т.е. сумма величин xij, умноженных на соответствующие стоимости cij должна быть минимальной: L = c 11 x 11 + c 12 x 12 +... + c 1 n x 1 n + + c 21 x 21 + c 22 x 22 +... + c 2 n x 2 n +... + + cm 1 xm 1 + cm 2 xm 2 +... + cmnxmn = min, или, гораздо короче,
где знак двойной суммы Функция (3.31) линейна, ограничения - равенства (3.29), (3.30) также линейны. Перед нами - типичная задача линейного программирования с ограничениями-равенствами (ОЗЛП). Как и всякую другую задачу линейного программирования, ее можно было бы решить симплекс-методом, но данная задача имеет некоторые особенности, позволяющие решить ее более просто. Причиной является то, чтовсе коэффициенты при переменных в уравнениях (3.29), (3.30) равны единице. Кроме того, имеет значение структура связей между условиями. Нетрудно убедиться, что не все m+n уравнений нашей задачи являются независимыми. Действительно, складывая между собой все уравнения (3.29) и все уравнения (3.30), мы должны получить одно и то же, в силу условия (3.28). Таким образом, условия (2), (3) связаны одной линейной зависимостью, и фактически из этих уравнений только m+n -1, а не m+n являются линейно независимыми. Значит, ранг системы уравнений (3.29), (3.30) равен r = m+n - 1, а, следовательно, можно разрешить эти уравнения относительно m+n -1 базисных переменных, выразив их через остальные, свободные. Подсчитаем количество свободных переменных. Оно равно: k = mn - (m + n - 1) = mn - m - (n - 1) = m (n - 1) - (n - 1) = (m - 1) (n - 1). Мы знаем, что в задаче линейного программирования оптимальное решение достигается в одной из вершин ОДР, где по крайней мере(m -1) (n -1 ) значений xij должны быть равны нулю. Условимся о терминологии. Значения xij количества единиц груза, направляемых из пункта Ai в пункт Bj мы будем называть перевозками. Любую совокупность значений (xij) (i = 1,..., m; j = 1,..., n) будем называть планом перевозок, или просто планом. План (xij) будем называть допустимым, если он удовлетворяет условиям (3.29), (3.30) (так называемым «балансовым условиям»): все заявки удовлетворены, все запасы исчерпаны. Допустимый план будем называть опорным, если в нем отличны от нуля не более r = m+n -1 базисных перевозок xij, а остальные перевозки равны нулю. План (xij) будем называть оптимальным, если он, среди всех допустимых планов, приводит к наименьшей стоимости всех перевозок. Перейдем к изложению методов решения транспортной задачи (ТЗ). Эти методы не требуют манипуляций с симплекс-таблицами, а сводятся к более простым операциям непосредственно с таблицей, где в определенном порядке записаны все условия ТЗ. Такую таблицу мы будем называть транспортной таблицей. В транспортной таблице записываются - пункты отправления и назначения, - запасы, имеющиеся в пунктах отправления, - заявки, поданные пунктами назначения, - стоимости перевозок из каждого пункта отправления в каждый пункт назначения. Стоимости перевозок мы будем помещать в правом верхнем углу каждой ячейки, с тем чтобы в самой ячейке при составлении плана помещать перевозки xij. Образец транспортной таблицы дан в табл.3.8. Для краткости в дальнейшем будем обозначать пункты отправления - ПО, пункты назначения - ПН. В правом верхнем углу каждой клетки проставлены стоимости перевозки единицы товара (груза) из ПО Аi в ПН Bj. В правом столбце помещены запасы товара в каждом ПО, в нижней строке - заявки, поданные каждым ПН. Для ТЗ сумма запасов равна сумме заявок; общее значение этой суммы записывается в правой нижней ячейке таблицы. Таблица 3.8
Выше мы показали, что ранг системы уравнений-ограничений ТЗ равен r = m+n -1, где m - число строк, а n - число столбцов транспортной таблицы. Значит, в каждом опорном плане, включая оптимальный, будут отличны от нуля не более, чем m+ n -1 перевозок. Ячейки (клетки) таблицы, в которых мы будем записывать эти отличные от нуля перевозки, условимся называть базисными, а остальные (пустые) свободными. Таким образом, решение ТЗ свелось к следующему. Найти такие значения положительных перевозок, которые, будучи проставлены в базисных клетках транспортной таблицы, удовлетворяли бы следующим условиям: - сумма перевозок в каждой строке таблицы должна быть равна запасу данного ПО; - сумма перевозок в каждом столбце должна быть равна заявке данного ПН; - общая стоимость перевозок - минимальная. В дальнейшем все действия по нахождению решения ТЗ будут сводиться к преобразованию транспортной таблицы 3.8. При описании этих преобразований нам удобно будет пользоваться нумерацией клеток таблицы (подобной нумерации клеток шахматной доски). Клеткой (Аi,Bj) или, короче, клеткой (i,j) мы будем называть клетку, стоящую в i -й строке и j -м столбце транспортной таблицы. Например, самая верхняя левая клетка будет обозначаться (1,1), стоящая под ней (2,1) и т.д. 3.5.2. Нахождение опорного плана Решение транспортной задачи, как и всякой задачи линейного программирования, начинается с нахождения опорного решения, или, как мы будем говорить, опорного плана. В отличие от общего случая ОЗЛП с произвольными ограничениями и минимизируемой функцией, решение ТЗ всегда существует. Построение опорного плана. Воспользуемся так называемым «способом северо-западного угла». Пояснить его проще всего будет на конкретном примере. Пример 1. Условия ТЗ заданы транспортной таблицей (см. табл.3.9)
Таблица 3.9
Требуется найти опорное решение ТЗ (построить опорный план). Решение. Перепишем табл.2 и будем заполнять ее перевозками постепенно, начиная с левой верхней ячейки (1,1) («северо-западного угла» таблицы). Будем рассуждать при этом следующим образом. Пункт B1 подал заявку на 18 единиц груза. Удовлетворим эту заявку за счет запаса 48, имеющегося в пункте А 1, и запишем перевозку 18 в клетке (1,1). После этого заявка пункта В 1 удовлетворена, а в пункте А 1 осталось еще 30 единиц груза. Удовлетворим за счет них заявку пункта В 2 (27 единиц), запишем 27 в клетке (1,2); оставшиеся 3 единицы пункта А 1 назначим пункту В 3 В составе заявки пункта В 3 остались неудовлетворенными 39 единиц. Из них 30 покроем за счет пункта А 2, чем его запас будет исчерпан, и еще 9 возьмем из пункта А3. Из оставшихся 18 единиц пункта А 3 12 выделим пункту В 4; оставшиеся 6 единиц назначим пункту В 5, что вместе со всеми 20 единицами пункта А 4 покроет заявку (см. табл.3.10). На этом распределение запасов закончено: каждый пункт назначения получил груз согласно своей заявке. Это выражается в том, что сумма перевозок в каждой строке равна соответствующему запасу, а в столбце - заявке. Таким образом, нами сразу же составлен план перевозок, удовлетворяющий балансовым условиям. Полученное решение является не только допустимым, но и опорным решением транспортной задачи. Таблица 3.10
Клетки таблицы, в которых стоят ненулевые перевозки, являются базисными, их число удовлетворяет условию r = m+n - 1 = 8. Остальные клетки - свободные (пустые), в них стоят ненулевые перевозки, их число равно (n - 1)(m - 1) = 12. Значит, наш план - опорный и поставленная задача построения опорное плана решена.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 1212; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |





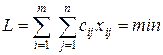
 означает, что суммирование производится по всем комбинациям индексов (i = 1,..., m; j = 1,..., n), т.е. по всем комбинациям пунктов отправления с пунктами назначения.
означает, что суммирование производится по всем комбинациям индексов (i = 1,..., m; j = 1,..., n), т.е. по всем комбинациям пунктов отправления с пунктами назначения.


