
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование транспортной сетиСодержание книги Поиск на нашем сайте
Эта задача встречается на практике наиболее часто и является одной из наиболее важных. Задача формулируется так Имеются отправители грузов Ai, А2...Ai...Am с имеющимся у каждого отправителя количеством груза a1, а2...аi...аm тонн. Имеются получатели груза В1 B2...Bj...Bn с требуемым каждому количеством груза в1 в2...вj..вn тонн. Каждый отправитель может удовлетворить запросы любого получателя. Расстояния между отправителями и получателями известны и составляют Условие задачи записывается в виде таблицы 1. Таблица 1 Матрица условий
где Хij - количество тонн груза предназначенного к отправке из Аi, в Вj, а так как потребность пункта Вj, составляет bj тонн, то
Сказанное справедливо для любого пункта Вj, поэтому получаем систему п- уравнений:
С другой стороны общее количество груза, отправляемого из пункта Аi, во все пункты назначения Вj, составит
По условиям задачи эта сумма равна наличию груза в пункте Аi.
Сказанное справедливо к любому пункту отправления, имеем т аналогичных (1) уравнений:
Более компактно уравнения (1) и (2) записываются в форме
Суммарная транспортная работа Р из условий, таким образом, равна
Таким образом, в математической форме транспортная задача требует определения значений переменных Хij, минимизирующих линейную формулу
При этом суммарное количество груза у отправителей должно быть равно количеству, требуемому получателю
Транспортная задача линейного программирования и её применение при решении автотранспортных задач Рассмотрим метод потенциалов. Этот метод рекомендуется использовать в курсовом проектировании. Метод потенциалов реализуется с помощью строго регламентированной процедуры вычислений - алгоритма метода. При этом все вычисления производят в таблице-матрице, составленной по условиям задачи, представленной на рисунке 1. Задача формулируется так: имеется ряд поставщиков транспортно-однородного груза и ряд потребителей этого груза. Требуется получить такой план закрепления, чтобы при перевозке грузов транспортная работа (ткм) была минимальной. Так как оптимизации подлежит транспортная работа, поэтому в качестве затрат в матрицу вводится расстояние между всеми пунктами. Для решения задач по составлению оптимальных планов закрепления необходимо провести подготовительную работу, заключающуюся в определении следующих исходных данных: 1. Наименование грузоотправителей и объём поставок грузов. 2. Наименование грузополучателей и объёмы потребления. 3. Расстояние перевозки от каждого грузоотправителя до каждого получателя. На основании исходных данных формируется матрица (табл.2).
Таблица 2 Матрица условий
Рассмотрим решение задачи на конкретном примере. Потребителям В1, В2, В3 и В4 требуется песок в количестве 30, 70, 40 и 30 тонн. На складах поставщиков А1 А2, и А3 имеется соответственно 80, 50 и 40 тонн. Расстояния 1ij между ними указаны в таблице-матрице, которую составляем. В правых верхних углах записаны расстояния между поставщиками и потребителями. Каждая из клеток представляет собой реальные маршруты перевозок груза в процессе решения задачи. В средней части этих клеток будут записываться значения Хij>0, где Хij Значения Хij делятся на основные Хij >0 и не основные Хij <0. Основные Хij, записанные в матрице, обычно называют загрузками, а клетки, в которых они записаны, называются занятыми. Клетки матрицы без загрузок называют незанятыми. В матрице также предусмотрены вспомогательные столбцы Для удобства подсчётов тонны заявленного груза переводят в ездки (для существа задачи это безразлично). Составляем допустимый исходный план следующим порядком. Три ограничения, которые представлены в математической записи линейного программирования: - полное обеспечение всех потребностей; - полный вывоз всего груза; - неотрицательность любой поставки. Если все эти требования не выполняются, то задача не решается. 1. Сначала планируем перевозки с первого склада (А1) ближайшим потребителям. 2. Затем со второго склада (А2) ближайшим потребителям и т. д. заполняем таблицу. Проводится это способом минимального элемента по строке следующим образом Переходим к перераспределению груза со склада А2. В первую очередь, удовлетворяем ближайшего, ещё не удовлетворённого потребителя. Им является потребитель В1 (4 км), которому требуется 30 тонн груза (10 тонн было завезено со склада А1), поэтому со склада А2 мы можем поставить 20 тонн груза, полностью удовлетворив потребителя В1. На складе А2 осталось 30 тонн груза, следующий ближайший потребитель является В2, которому требуется 70 тонн груза. Оставшиеся 30 тонн получает потребитель В2. Со склада А3 направляем оставшиеся 40 тонн потребителю В2. Таким образом, потребности всех потребителей полностью удовлетворены, а со всех складов полностью вывезены все запасы груза. На этом этапе вычисления закончены. 3. Вычисляется транспортная работа, которая будет равна Р=10-9+40-5+30-8+204+30-9+4022=1760тонно-км. В таблице 3 представлен исходный допустимый план перевозок. Таблица 3 Исходный допустимый план перевозок
Проверяем заполненность матрицы, т. е. число заполненных клеток по критерию m+n-1. Если число клеток отличается от числа по критерию и матрица является вырожденной, по ней проводить дальнейшие расчёты невозможно. Необходимо откорректировать матрицу. Если заполненных клеток не хватает, то добавляем в клетки фиктивную нагрузку 0 т. Если клетки лишние, то их число уменьшаем методом, описанным ниже. Проверка разработанного плана на оптимальность состоит из двух этапов: на первом этапе вычисляются вспомогательные индексы - Ui и Vj, а на втором этапе исследуются незанятые клетки на потенциальность с целью определения суммы индексов
- для каждой занятой клетки матрицы сумма, соответствующей ей индексов U и V, равна расстоянию в данной клетке, т. е. Ui + Vj = Lij, где Lij - расстояние в клетке. Это даёт возможность при известном одном индексе определить значение другого.
Исследуем допустимый исходный план на оптимальность, для чего сравниваем во всех незанятых клетках расстояния Lij с суммой соответствующих ей индексов по критерию Lij ≥ Ui + Vj, т. е. расстояния должны быть больше или равны сумме индексов. Запишем в матрицу (табл. 3) Uj = 0, тогда в соответствии с формулами:
Далее
Таким образом, все вспомогательные индексы определены и можно приступить к проверке незанятых клеток на оптимальность. Эта проверка заключается в сравнении расстояния каждой незанятой клетки матрицы с суммой соответствующих ей индексов с целью выявления Ui + Vj>Lij.
Проверка показывает, что у незанятых клеток A3Bi и А3В3 расстояние меньше суммы индексов, следовательно, составленный допустимый исходный план не является оптимальным и подлежит улучшению. Выявленные клетки являются резервом улучшения плана, и поэтому их называют потенциальными, почему и рассматриваемый метод называют "методом потенциалов". Полученные потенциалы обозначим в матрице цифрой в квадратике (цифра - превышение индекса над расстоянием). Процедура улучшения неоптимального плана сводится к перемещению загрузок в потенциальные клетки матрицы. Поскольку нельзя просто перенести загрузку в клетках, не изменив суммарные значения по строкам и столбцам, то разработан специальный способ перемещения загрузок, не нарушающий загрузку строк и столбцов. Он заключается в составлении цепочки возможных перемещении загрузок в матрице, определении величины перемещения загрузки и самого перемещения. Такую цепочку можно построить всегда, причём единственным способом. Делается это так: - для клетки с наибольшим потенциалом (в нашем случае А3В3) строим замкнутую цепочку из горизонтальных и вертикальных линий так, чтобы одна её вершина лежала в потенциальной клетке, а все остальные вершины располагались бы в занятых клетках. Конфигурации цепочки могут быть разной формы, но только из вертикальных и горизонтальных клеток. - составив цепочку, помечают знаком (+) её нечетные вершины (считая первой в потенциальной клетке) и знаком (-) чётные вершины. Наименьшая из чётных загрузок определяет величину перемещаемой загрузки (в нашем случае 20 т). - переместив эту загрузку из клетки со знаком (-) в клетку со знаком (+), получаем новый вариант плана с меньшей транспортной работой (табл. 4). Величины новых перемещений представлены в квадратиках. Таблица 4
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 361; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.177.204 (0.008 с.) |

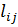 км. Общее количество грузов, имеющееся у отправителей и требуемое получателю, равно.
км. Общее количество грузов, имеющееся у отправителей и требуемое получателю, равно. Количество тонн груза для доставки в пункт Вj, из всех пунктов отправления равно
Количество тонн груза для доставки в пункт Вj, из всех пунктов отправления равно




 (2)
(2)
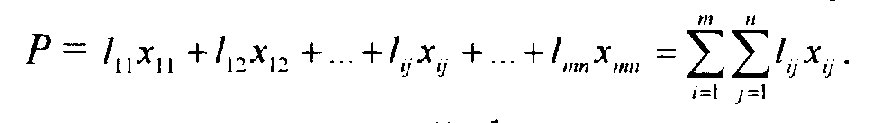


 Рис. 5. Алгоритм метода
Рис. 5. Алгоритм метода 
 объём поставок, в крайних случаях в эти клетки могут записываться и не основные поставки
объём поставок, в крайних случаях в эти клетки могут записываться и не основные поставки  80 тонн. Запрос удовлетворяется полностью на складе остаётся ещё 40 тонн, которые направляем к следующему ближайшему потребителю. Им оказывается потребитель В4, которому требуется 30 тонн груза. Полностью удовлетворяем запрос и этого потребителя, а на складе А1 остаётся 10 тонн, которые направляем к следующему ближайшему (последнему) потребителю В1 которому требуется 30 тонн груза, таким образом весь груз со склада А1 вывезен полностью.
80 тонн. Запрос удовлетворяется полностью на складе остаётся ещё 40 тонн, которые направляем к следующему ближайшему потребителю. Им оказывается потребитель В4, которому требуется 30 тонн груза. Полностью удовлетворяем запрос и этого потребителя, а на складе А1 остаётся 10 тонн, которые направляем к следующему ближайшему (последнему) потребителю В1 которому требуется 30 тонн груза, таким образом весь груз со склада А1 вывезен полностью.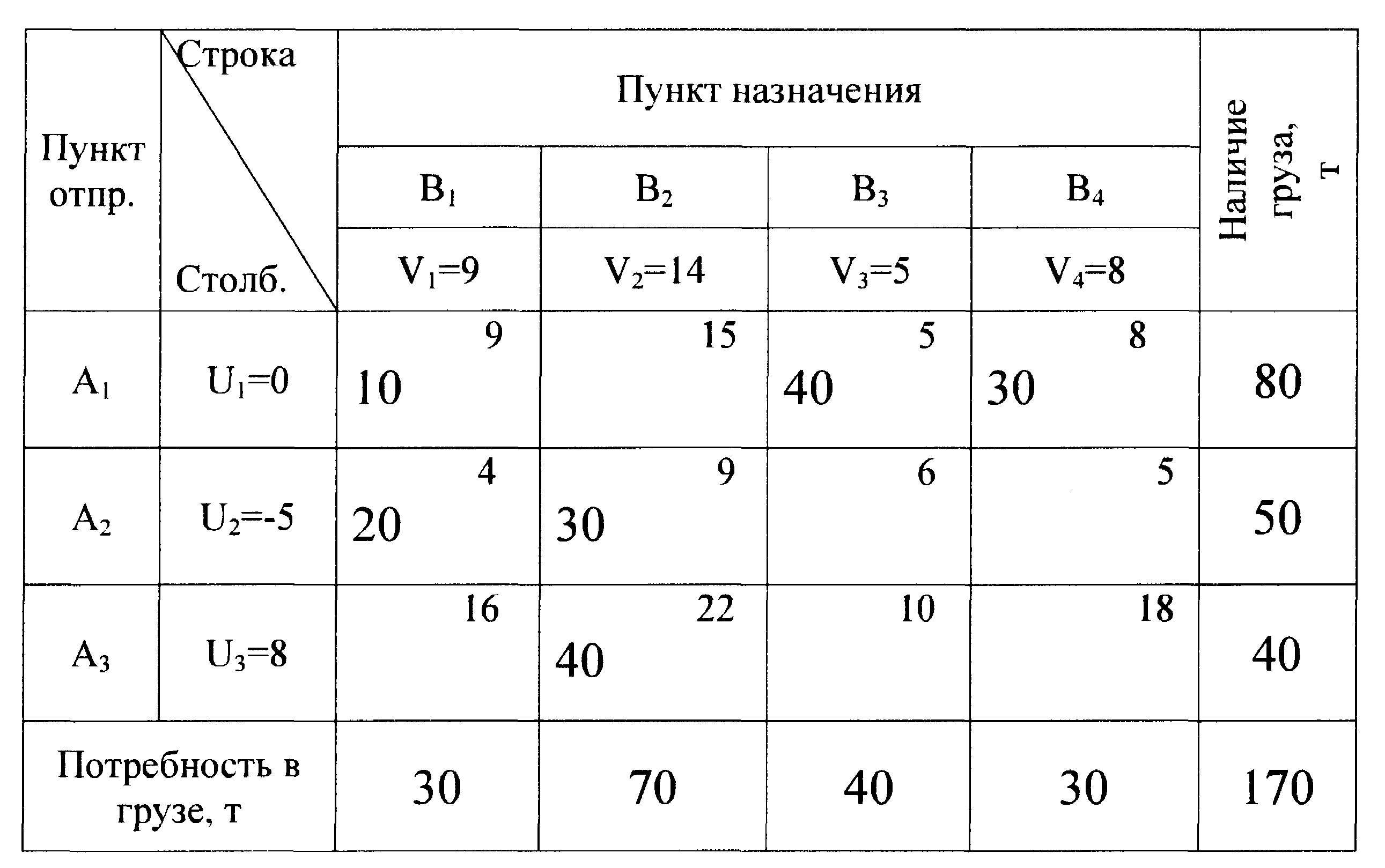
 . Рассчитываем на матрице специальные индексы U и V и заносим их в строку и столбец матрицы. Для определения индексов используются следующие правила:
. Рассчитываем на матрице специальные индексы U и V и заносим их в строку и столбец матрицы. Для определения индексов используются следующие правила: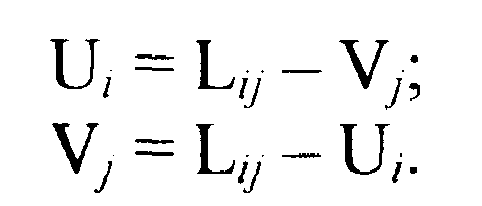 (5)
(5)





