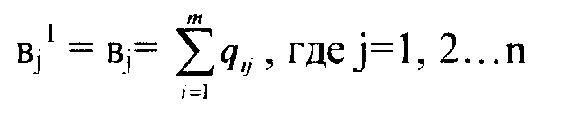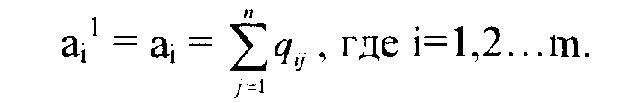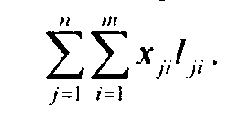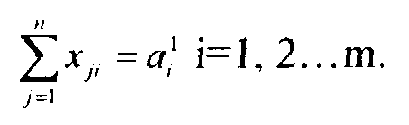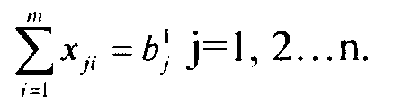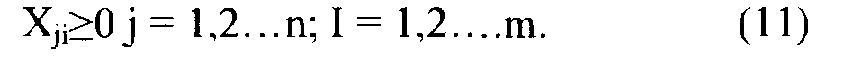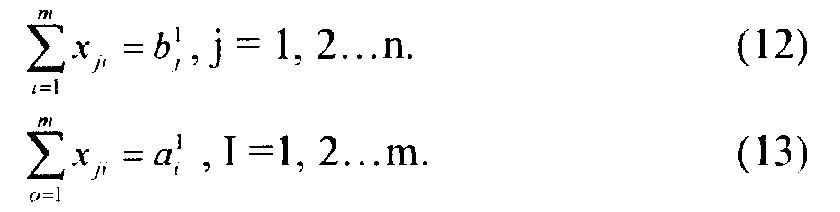Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прогнозирование перевозок грузовСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
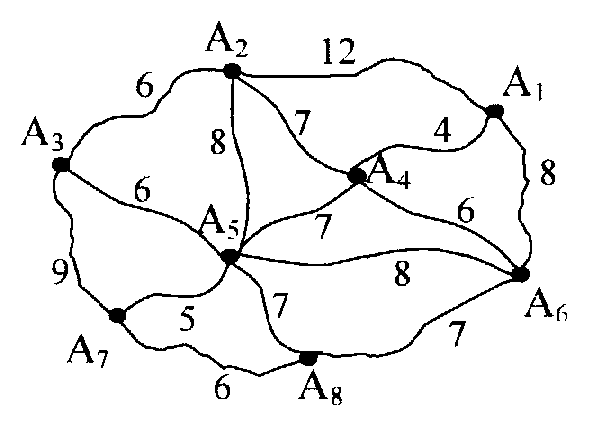
Одним из важнейших факторов, оказывающих влияние на эффективность использования транспортных средств, является расстояние перевозки, от величины которого зависит количество транспортной работы. Многочисленными исследованиями доказано, что, чем меньше будет выполняться транспортной продукции, измеряемой в тонно-километрах, тем лучше для хозяйства страны. Это связано с тем, что сокращение транспортной работы сопровождается снижением транспортных затрат и уменьшением потребности в транспортных средствах. Поэтому перевозки грузов для всех отраслей хозяйства должны осуществляться по возможности на короткие (оптимальные) расстояния. Большая часть перевозок грузов осуществляется по сложившейся сети дорог и улиц с конкретными условиями эксплуатации подвижного состава и организации движения. Практически между двумя пунктами, расположенными на транспортной сети региона может быть множественное число вариантов проезда, которым соответствуют определённые расстояния, скорости и время. Из теории известно, что максимальную производительность однотипного подвижного состава можно получить на том маршруте, где будут минимальные затраты времени. Однако критерий, по которому находят оптимальное решение, определяется не только затратами времени, а той целью, которую необходимо достигнуть при решении задачи оптимального варианта проезда. Наиболее часто в качестве критерия принимается минимум суммарного пробега, так как при одинаковых условиях движения на всех участках маршрута план, оптимальный по пробегу, будет оптимальным по затратам времени и стоимости. Не применяя никаких вычислений, кратчайший путь между двумя пунктами можно выбрать в том случае, если они находятся в пределах видимости. Если же они достаточно удалены друг от друга, то возникают различные варианты передвижения, которые необходимо сравнить, чтобы выбрать наилучший. Решение такой задачи осуществляется методом потенциалов. Транспортная сеть состоит из пунктов А1,А2...Аi и дорог её соединяющих. Длины участков между каждой парой пунктов известны и равны lij. Из начального пункта в конечный можно попасть по множеству маршрутов, требуется найти путь наименьшей протяжённости. Рассмотрим процедуру вычислений, определив кратчайшее расстояние от пункта А1 до всех остальных по сети дорог, представленных на рисунке 5.
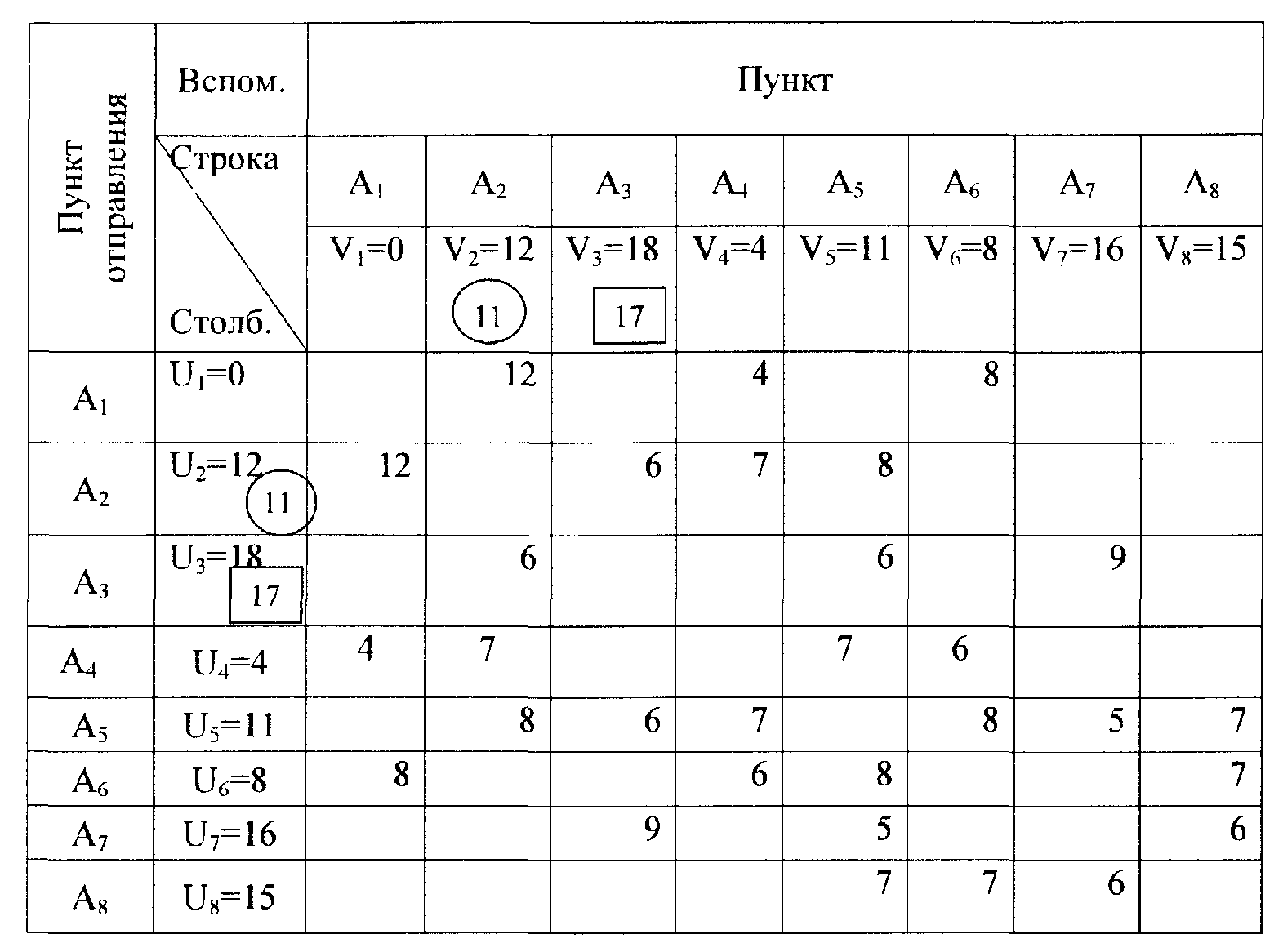
Рис. 5. Схема транспортной сети Построив модель транспортной сети, замеряем расстояния между ближайшими (соседними) пунктами. Составим матрицу (табл.15) Таблица 15 Матрица условий
(исходный вариант), заполняя расстояния между соседними пунктами. При дальнейших расчётах пользуемся следующим правилом. Каждому пункту Aj соответствует некоторое число Vj, характеризующее расстояние от пункта Aj до пункта Аj. Приступаем к нахождению индексов, используя правила Vj = Ui; Vj= Ui+lij. 1. Принимаем индекс U1=V1=0. 2. По правилу находим через А1А2, A1A4 и А1А6 V2=0+12=12, V4=0+4=4, V6=0+8=8 и Vj= Ui. U2=V2=12, U4=V4=4, U6=V6=8 и заносим в таблицу 16. 3. Находим V3 через А2А3 с известным U2: V3=U2+123=12+6=18 и V3=U3=18. 4. V5 =min (по столбцу) =11, V5 =U5 =11. 5. V7=min (по столбцу) =16, V7=U7 =16. 6. V8=min (по столбцу) =A6AS =15, V8=U8=15. Проверяем заполненные клетки таблицы на оптимальность по критерию lij В таблице 15 142 <V2 – U4 7<12–4=8, критерий не соблюдается, поэтому решение не оптимально. Рассчитываем новый индекс V2 по вышеуказанному критерию Vj = Ui+lij=4+7=11. Получаем U2=V2=11. Получаем новую таблицу (со значениями V2 U2 в кружках) и проверяем её на оптимальность. Она не оптимальна, так как l53 Определяем новый индекс V3=U5+l53 =11+6=17, U3=V3=17. Проверка таблицы 15 (с индексом кружочек и квадратик) показывает, что решение оптимально. Следовательно, кратчайшее расстояние от точки А1 задано числами V2...V8, т. е. А1 - А2=11 км, A1 - А3=17 км........А1 - А8=15 км. Таблица (оптимальная) даёт также последовательность прохождения промежуточных пунктов, например из А1 в А7, и определяется следующим образом: 1. В столбце, соответствующему конечному пункту А7 отыскиваем заполненную клетку, у которой расстояние равно разности индексов столбца и строки lij=Vj-Ui (у нас А5А7). Она означает последнее звено маршрута А5-А7. 2. Для определения предпоследнего операция повторяется для столбца А5. Это будет звено А4-А5. 3. Затем перед ним по столбцу А4 звено А1-А4. Итак, А1®А4®А5®А7 кратчайший путь найден. Затем повторяем все решения с самого начала (всю матрицу), принимая: а) исходный пункт А2 (т.е. V2=U2=0); б) исходный пункт А3 (V3=U3=0) и т. д. определяем все кратчайшие расстояния.
Одной из важнейших задач оперативного планирования перевозки грузов автомобильным транспортом является увязка грузопотоков в маршруты. Решение этой задачи позволяет снизить непроизводительные пробеги автомобилей, поэтому в практике оперативного планирования перевозок грузов на автотранспорте, как правило, после закрепления потребителей за поставщиками, обеспечивающего минимизацию транспортной работы, решается другая задача - маршрутизация. В общем виде она формулируется так: при постоянных множествах пунктов производства, потребления, размещения подвижного состава, объёма поставок и потребления грузов и ограничениях на ресурсы подвижного состава необходимо найти допустимые, т. е. удовлетворяющие налагаемым практикой планирования ограничениям и упорядоченные подмножества связанных пунктов, при реализации которых достигается экстремальное значение целевой функции, отражающей эффективность процесса поставок грузов. В настоящее время ярко выраженная разница в технологии перевозок разделяет методы маршрутизации на два класса: маршрутизация помашинных отправок грузов и маршрутизация мелких партий грузов. Задача маршрутизации помашинных отправок возникает в тех случаях, когда у любого отправителя каждый отдельный автомобиль загружается полностью в адрес только одного потребителя. Примером таких перевозок являются перевозки различных массовых навалочных грузов, кирпича, леса и т.п. Решение состоит из двух этапов: оптимального решения транспортной задачи и формирования набора маршрутов. Технология конструирования маршрутов может быть выполнена методом совмещённых планов, разработанным на базе линейного программирования. Идея метода совмещённых планов (матриц) состоит в следующем. На первом этапе ищем оптимальный план холостых пробегов автомобилей (как это делалось при решении задачи по закреплению потребителей за поставщиками). На втором этапе в одну матрицу записываем два плана: заданный и полученный, после чего путём специальной процедуры выбираем маршруты движения автотранспорта. В простейшей постановке задача маршрутизации грузовых перевозок состоит в следующем. Разнородный груз сосредоточен в пунктах отправления А1, A2...Ai...Am в количествах соответственно а1, a2...ai…am единиц. Его необходимо доставить в пункты назначения В1,B2...Bj...Bn в количествах в1, в2…вj...вn соответственно. Объём перевозок из i-го пункта отправления в j-й пункт назначения составляет qijединиц и известен для всех пунктов. Расстояние от i-ro пункта отправления до j-ro пункта назначения равно lij и известно для всех комбинаций ij. В процессе выполнения перевозок в пунктах назначения В1, B2...Bj...Bn после разгрузки автомобилей будет образовываться порожняк в количествах Этот порожняк необходимо подать под очередную загрузку в пункты отправления А1, А2...Аi...Аm в количестве Величины аi, вj, qij, Количество прибывающих в пункт назначения гружёных автомобилей представляет ресурсы порожняка в данном пункте. Количество убывающих из пункта отправления гружёных автомобилей - потребность этого пункта в порожняке.
По смыслу рассматриваемой задачи всегда имеет место условие
Расстояние от Bj до Аi, равное lji=ljj, известно для всех сочетаний i, j. За смену каждый автомобиль выполняет несколько ездок с грузом из одного или нескольких пунктов отправления в один или несколько пунктов назначения. После каждой ездки с грузом автомобиль возвращается в пункт отправления порожняком. Из каждого пункта назначения автомобиль может следовать под погрузку в любой пункт отправления, имеющий груз. Дополнительным условием задачи является требование, чтобы за рабочую смену автомобиль направлялся не более чем в 4 разных пункта отправления и такое же количество пунктов назначения. Практически это означает, что при сменном задании с большим числом ездок необходимо составлять кольцевой маршрут так, чтобы по нему можно было сделать несколько оборотов. Таким образом, требуется составить такой план перевозок (маршруты движения автомобилей и сменные задания водителям), который обеспечит выполнение заданных объёмов перевозок с наименьшим холостым пробегом автомобилей. Обозначим количество порожняка в автомобилеездках, подаваемого из пункта Bj в пункт Ai, через xij. Суммарный холостой пробег автомобилей из всех пунктов наличия порожняка во все пункты его подачи при этом составит
Условие полного удовлетворения спроса на порожняк каждого пункта отправления за счёт подачи из разных пунктов наличия порожняка записывается следующим образом:
Весь порожняк из каждого пункта назначения должен быть подан в пункты отправления под погрузку. Формально это означает, что
Количество автомобилей не может быть отрицательным, т. е.
Таким образом, требуется определить совокупность величин х,; (план возврата порожняка), удовлетворяющих условиям
и минимизирующих суммарный холостой пробег автомобилей
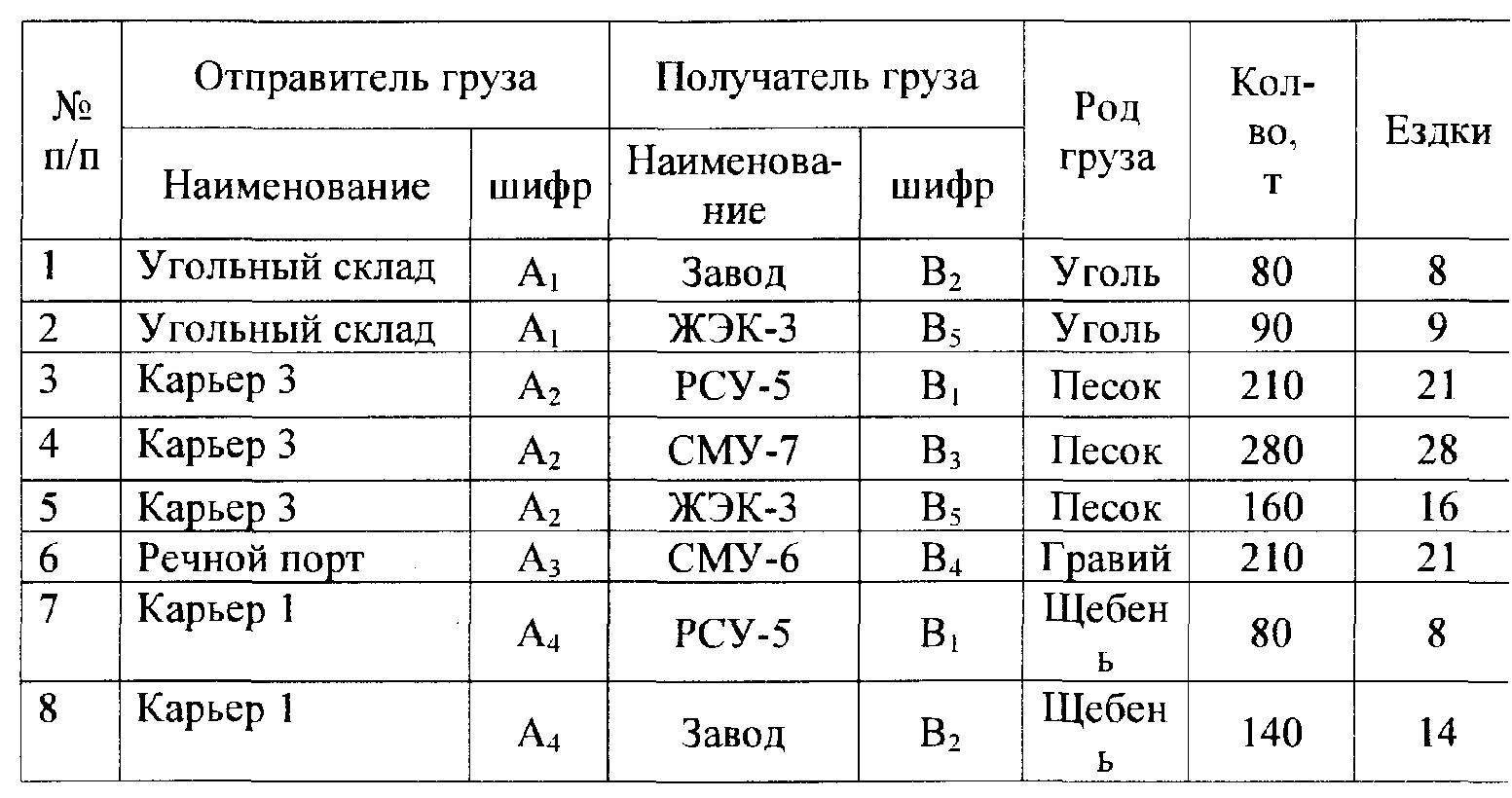
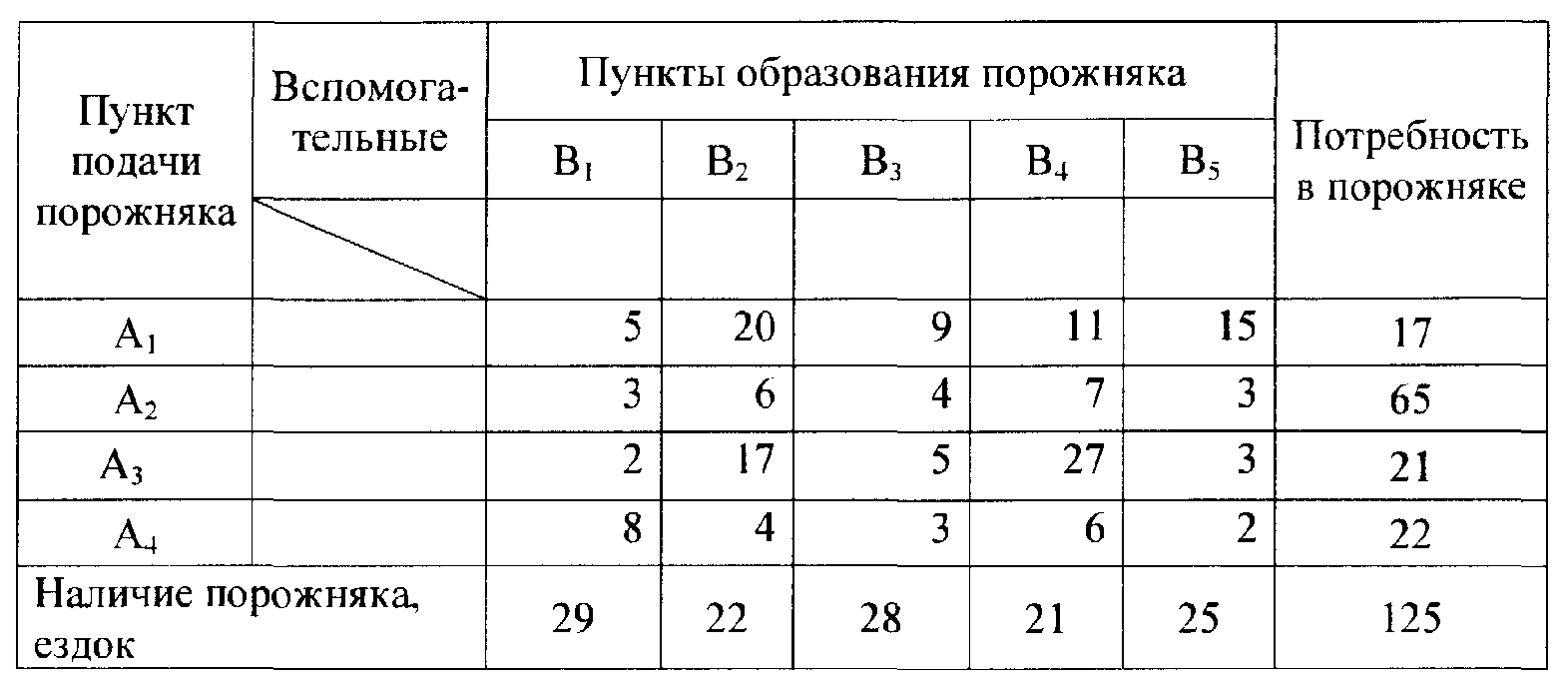
По смыслу задачи имеет место равенство Сформулированная задача (11 - 14) называется задачей минимизации холостых пробегов автомобилей. Это транспортная задача линейного программирования, имеющая n∙m число переменных, связанных посредством n+m линейных уравнений. Далее рассмотрим постановку указанной задачи на конкретном примере - задания на перевозку грузов на известные расстояния. Исходные данные приведены в таблице 16. Таблица 16 Исходные данные
Расстояния между всеми пунктами заданы в табл.17 (матрица расстояний).
Таблица 17 Матрица расстояний
Решение поставленной задачи рассматриваемым методом совмещённых планов включает три этапа.
Этап 1. Минимизация холостых пробегов автомобилей и нахождение оптимального плана возврата порожних автомобилей под погрузку после их выгрузки. Используя данные таблицы 16 и таблицы 17, составляем матрицу условий (табл. 18) Таблица 18 Матрица условий
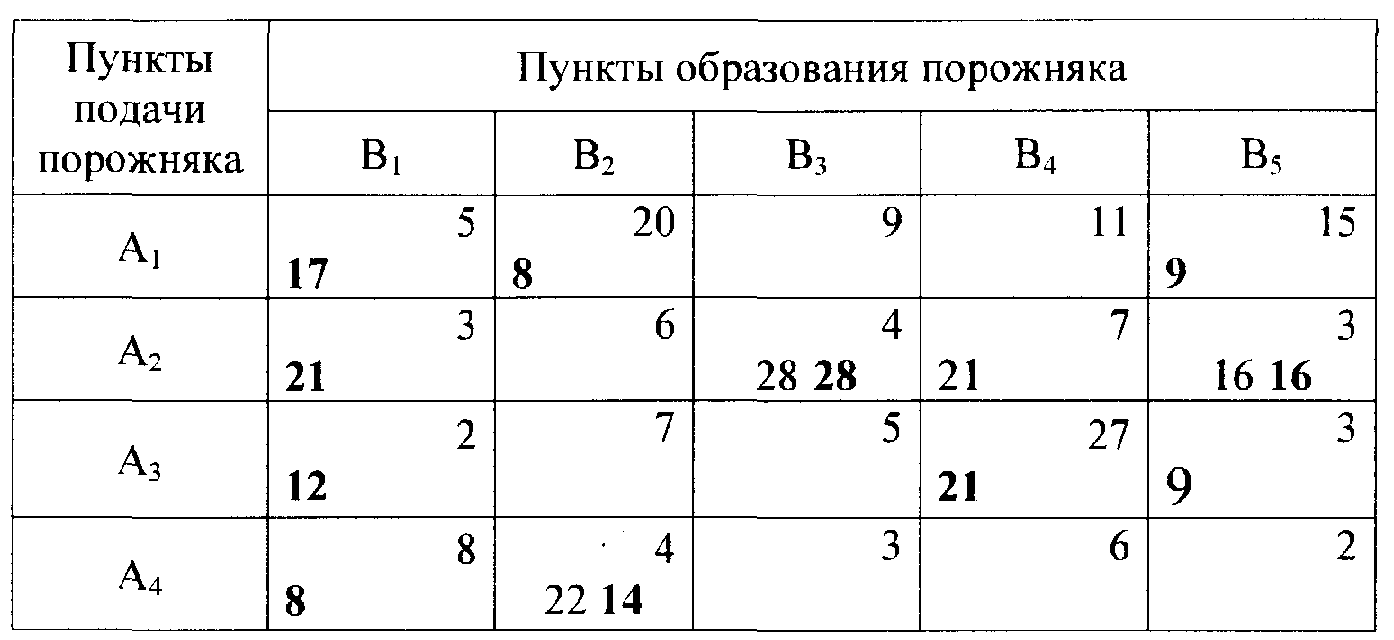
В соответствии с алгоритмом метода потенциалов находим допустимый план холостых пробегов. Затем через построение цепочек перемещений составляем улучшенный план холостых пробегов и, наконец, получаем оптимальный план возврата порожних автомобилей. Этот оптимальный план возврата порожняка представлен в таблице 19. Таблица 19 Оптимальный план возврата порожняка под погрузку
Этап 2. Составляем матрицу совмещённых планов (табл.20).
Таблица 20 Матрица совмещённых планов
Для этого в матрицу возврата порожняка (т.е. холостых пробегов) таблицу 19 записываем число гружёных ездок из таблицы16 исходных данных. В разбираемом примере ездки с грузом обозначены жирным шрифтом, а порожние - обычным. Вспомогательные и итоговые строки и столбцы для дальнейших расчётов не нужны, и поэтому они исключены из матрицы. Маршруты движения автомобилей строятся непосредственно на матрице совмещённых планов, таблице 20. При этом сначала выбираются все маятниковые маршруты, а затем все кольцевые. Маятниковые маршруты определяют клетки с двойной загрузкой, т. е. клетки, в которых записаны одновременно ездки с грузом и без груза. В нашем примере двойные загрузки имеют клетки А2В3, А2В5 и А4В2, которые обозначают следующие маятниковые маршруты: маршрут 1 А2 - В3 - А2 на 28 ездок; маршрут 2 А2 - В5 - А2 на 16 ездок; маршрут 3 А4 - В2 - Ад на 14 ездок. Количество ездок по каждому маятниковому маршруту определяется наименьшей из загрузок рассматриваемой клетки. Запланированные на маршруты 1 - 3 гружёные и порожние ездки исключаются из матрицы, после чего продолжается составление маршрутов. Поскольку в матрице теперь отсутствуют клетки с двойной загрузкой, приступаем к составлению кольцевых маршрутов. Кольцевые маршруты из четырёх звеньев (две ездки с грузом и две без груза) составляются следующим образом: из горизонтальных и вертикальных отрезков строят прямоугольник так, чтобы все его нечётные вершины лежали в клетках с гружёными, а чётные - в клетках с порожними ездками. Вершины прямоугольника обозначают кольцевой маршрут с двумя пунктами отправления и двумя пунктами назначения. Количество оборотов по маршруту определяется наименьшей из загрузок, обозначающих вершины прямоугольника. Таблица 21
|
||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 659; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.134.63 (0.014 с.) |

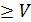 j – Ui.
j – Ui.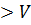 3 -U5 6<18-11.
3 -U5 6<18-11.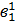 ,
, 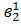 …
… 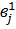 …
… 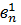 единиц.
единиц.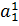 ,
, 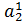 …
… 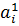 …
… 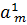 .
.