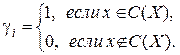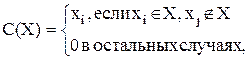Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции над функциями выбораСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В теории принятия решений введены следующие операции над функциями выбора: объединение, пересечение и дополнение. Объединение функций выбора С 1 и С 2 – функция С, определяемая формулой С (X)= C 1(X)È C 2(X). Пересечение функций выбора С 1 и С 2 – функция С, определяемая формулой С (X)= C 1(X)Ç C 2(X). Дополнение функции выбора С 1 – функция
Декомпозиция функций выбора Общие и частные декомпозиции. Общие декомпозиции. Исследуя связь между функциями выбора и бинарными отношениями, установим возможность декомпозиции произвольной функции выбора на нормальные функции. Нормальная функция выбора C (X) - это функция выбора, порожденная бинарным отношением R ÍW2 Декомпозиция 1. Пусть R 1,..., Rk - бинарные отношения на W; y(g1, …, gk) – булева функция (функция аргументами которой являются 0 и 1). Определим функцию выбора C = C (R l,..., Rk; y) на W:
где
Функцию выбора C = C (R 1,..., Rk; y), определенную формулами (2.3) и (2.4), назовем y - композицией нормальных функций выбора, порожденных бинарными отношениями R 1,..., Rk). Декомпозиция 2. Функцию выбора С, определяемую соотношением
назовем функцией разрешения и обозначим через С +. Функцию С:
назовем функцией запрета и обозначим через С -. Смысл функций разрешений и запретов очевиден. Именно, при функции разрешения элемент хi выбирается из X тогда и только тогда, когда в X входит и элемент хj, при функции запрета элемент хi выбирается из X тогда и только тогда, когда xj не входит в X. Частные декомпозиции. Декомпозиция 3. Введем следующие понятия. Булева функция yм(g1, …, gk) = Ú g1, …, gk, где дизъюнкция берется по всем наборам, называется мажоритарной или функцией голосования. Название объясняется тем, что YМ = 1 тогда я только тогда, когда больше половины переменных равны 1 (правило большинства). Функция выбора вида C (R 1,..., Rk; y м) называется мажоритарно-нормальной (МНФ). Таким образом, класс МНФ составляют все те функции выбора, которые получаются правилом выбора большинства из нормальных. Элемент х выбирается из X тогда и только тогда, когда он выбирается более чем половиной из функций выбора, порожденных бинарными отношениями R1,..., Rk. Декомпозиция 4. Пусть снова R 1,..., Rk - бинарные отношения на W. Положим
Функцию вида C (R 1,..., Rk; y s) называется - суммарно-нормальной функцией (СНФ). Декомпозиция 5. Введем понятие конечно-нормальных функций выбора. Конечно-нормальной функцией называется функция, которая представима произведением конечного числа нормальных функций выбора.
Множество таких функций выбора образует класс конечно-нормальных функций (КНФ). Декомпозиция 6. Из формул (2.3), (2.4) и (2.5) непосредственно следует, что
Тем самым приходим к понятию декомпозиции функции выбора в виде объединения нормальных.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 646; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.239.189 (0.006 с.) |

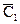 , определяемая формулой
, определяемая формулой