
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятности состояний Марковских моделей⇐ ПредыдущаяСтр 27 из 27
Множество состояний системы марковской цепи определенным образом классифицируются с учетом дальнейшего поведения системы: 1. Невозвратное множество В случае невозвратного множества возможны любые переходы внутри этого множества. Система может покинуть это множество, но не может вернуться в него. 2. Возвратное множество В этом случае также возможны любые переходы внутри множества. Система может войти в это множество, но не может покинуть его. 3. Эргодическое множество В случае эргодического множества возможны любые переходы внутри множества, но исключены переходы из множества и в него. 4. Поглощающее множество При попадании системы в это множество процесс заканчивается. Кроме описанной выше классификации множеств различают состояния системы: а) существенное состояние возможны переходы из Si в Sj и обратно б) несущественное состояние возможен переход из Si в Sj, но невозможен обратный. В некоторых случаях, несмотря на случайность процесса, имеется возможность до определенной степени управлять законами распределения или параметрами переходных вероятностей. Такие марковские цепи называются управляемыми. Очевидно, что с помощью управляемых цепей Маркова (УЦМ) особенно эффективным становится процесс принятия решений. Основным признаком детерминированной марковской цепи (ДМЦ) является детерминированность временных интервалов между отдельными шагами (этапами) процесса. Однако, часто в реальных процессах это свойство не соблюдается и интервалы оказываются случайными с каким-либо законом распределения, хотя марковость процесса сохраняется. Такие случайные последовательности называются полумарковскими. Кроме того, с учетом наличия и отсутствия тех или иных, упомянутых выше, множеств состояний, марковские цепи могут быть поглощающими, если имеется хотя бы одно поглощающее состояние, или эргодическими, если переходные вероятности образуют эргодическое множество. В свою очередь, эргодические цепи могут быть регулярными или циклическими. Циклические цепи отличаются от регулярных тем, что в процессе переходов через определенное количество шагов (цикл) происходит возврат в какое-либо состояние. Регулярные цепи этим свойством не обладают.
Далее будут рассмотрены простые однородные марковские цепи с дискретным временем. Основным математическим соотношением для ДМЦ является уравнение, с помощью которого определяется состояние системы на любом k -том ее шаге. Это уравнение имеет вид:
и называется уравнением Колмогорова-Чепмена. Уравнение Колмогорова-Чепмена относится к классу рекуррентных соотношений, позволяющих вычислить вероятность состояний марковского случайного процесса на любом шаге (этапе) при наличии информации о предшествующих состояниях. Дальнейшие математические соотношения зависят от конкретного вида марковской цепи. Поглощающие марковские цепи Как указывалось выше, у поглощающих ДМЦ имеется множество, состоящее из одного или нескольких поглощающих состояний. Для примера рассмотрим переходную матрицу, описывающую переходы в системе, имеющей 4 возможных состояния, два из которых являются поглощающими. Матрица перехода такой цепи будет иметь вид:
Практически важным является вопрос о том, сколько шагов сможет пройти система до остановки процесса, то есть поглощения в том или ином состоянии. Для получения дальнейших соотношений путем переименования состояний матрицу (7.4) переводят к блочной форме:
Такая форма позволяет представить матрицу (7.5) в каноническом виде:
где
На основании канонической формы (7.5а) получена матрица, называемая фундаментальной.
В матрице (7.6) символ (-1) означает операцию обращения, то есть
После соответствующих преобразований матрица (4) примет вид:
Каждый элемент матрицы (7.8) соответствует среднему числу раз попадания системы в то или иное состояние до остановки процесса (поглощения). Если необходимо получить общее среднее количество раз попадания системы в то или иное состояние до поглощения, то фундаментальную матрицу М необходимо умножить справа на вектор-столбец, элементами которого будут единицы, то есть
где Для иллюстрации приведем конкретный числовой пример: пусть известны значения переходных вероятностей матрицы П[3] с одним поглощающим состоянием: P 11 = 1; P 12 = P 13 = 0; P 21 = 0,25; P 22 = 0,5; P 23 = 0,25; P 31 = 0,5; P 32 = 0,5; P 33 = 0.
Рис. 7.1 Переходная матрица в блочной системе будет выглядеть так:
В данном случае
Проделаем необходимые вычисления:
В данном случае компоненты вектора М S означают, что если процесс начался с состояния S 2 общее среднее число шагов процесса до поглощения будет равно 3,34 и, соответственно, если процесс начинается с состояния S 3 , то - 2,26. В конкретных задачах, конечно, более информативным результатом будет не количество шагов, а какие-либо временные или экономические показатели. Этот результат легко получить, если связать пребывание в каждом состоянии с соответствующими характеристиками. Очевидно, набор этих характеристик составит вектор, на который нужно умножить М S слева. Так, если задать в нашем примере время пребывания в состоянии S 2 t 2 = 20 час, а в состоянии S 3 - t 3 = 30 час, то общее время до поглощения будет равно:
В случаях, когда марковская цепь включает несколько поглощающих состояний, возникают такие вопросы: в какое из поглощающих состояний цепь попадет раньше (или позже); в каких из них процесс будет останавливаться чаще, а в каких - реже? Оказывается, ответ на эти вопросы легко получить, если снова воспользоваться фундаментальной матрицей. Обозначим через bij вероятность того, что процесс завершится в некотором поглощающем состоянии Sj при условии, что начальным было состояние Si. Множество состояний bij снова образует матрицу, строки которой соответствуют невозвратным состояниям, а столбцы - всем поглощающим состояниям. В теории ДМЦ доказывается, что матрица В определяется следующим образом:
где М - фундаментальная матрица с размерностью S; R - блок фундаментальной матрицы с размерностью r. Рассмотрим конкретный пример системы с четырьмя состояниями S 1 - S 4, две из которых - S 1, S 2 - поглощающие, а две - невозвратные: S 3 и S 4 (рис.7.2): S 1 S 2 S 3 S 4
Рис. 7.2. Система с четырьмя состояниями Для наглядности и простоты вычислений обозначим переходные вероятности следующим образом: P 11 = P 22 = 1; P 31 = P 43 = q; P 34 = P 42 = P. Остальные значения вероятностей будут нулевыми. Каноническая форма матрицы перехода в этом случае будет выглядеть так:
или
Фундаментальная матрица после вычислений примет вид:
Тогда, матрица вероятностей поглощения вычисляется так:
Поясним вероятностный смысл полученной матрицы с помощью конкретных чисел. Пусть p = 0.7, а q = 0.3. Тогда, после подстановки полученных значений в матрицу В, получим:
Таким образом, если процесс начался в S 3, то вероятность попадания его в S 1 равна 0,38, а в S 2 - 0,62. Отметим одно интересное обстоятельство: несмотря на то, что, казалось бы, левое поглощающее состояние («левая яма») находится рядом с S 3, но вероятность попадания в нее почти в два раза меньше, чем в «удаленную яму» - S 2. Этот интересный факт подмечен в теории ДМЦ и объясняется он тем, что p > q, то есть процесс имеет как бы «правый уклон». Рассмотренная выше модель называется в теории ДМЦ моделью случайного блуждания. Такими моделями часто объясняются многие физические и технические явления и даже поведение игроков во время различных игр.
В частности, в рассмотренном примере объясняется факт того, что более сильный игрок может дать заранее значительное преимущество («фору») слабому противнику и все равно его шансы на выигрыш будут более предпочтительными. Кроме указанных выше средних характеристик вероятностного процесса с помощью фундаментальной матрицы можно вычислить моменты и более высоких порядков. В частности, дисперсия числа пребывания в том или ином состоянии - D определяется с помощью следующей матрицы:
где Мdg - диагональная матрица, т.е. матрица, полученная из М путем оставления в ней лишь диагональных элементов и замены остальных элементов нулями. Например, приведенная выше матрица (7.8) будет иметь вид:
В свою очередь, матрица М представляет собой матрицу, полученную из М путем возведения в квадрат каждого ее элемента, то есть для (7.8) будем иметь:
Аналогичным образом определяема и дисперсия для общего количества раз пребывания в том или ином состоянии М z, Обозначим ее D å.
Эргодические цепи Под эргодической ДМЦ понимается цепь, не имеющая невозвратных состояний. Таким образом, в такой цепи возможны любые переходы между состояниями. Напомним, что эргодические цепи могут быть регулярными и циклическими. Определение таких цепей было дано выше. Поскольку согласно данному выше определению в эргодической ДМЦ на любом шаге должны быть возможными любые переходы, то очевидно при этом, что переходные вероятности не должны равняться нулю. Оказывается, из этого условия вытекают некоторые замечательные свойства регулярных ДМЦ: 1. Степени П[ n ] k при к (r)0 стремятся к стохастической матрице A [ n ]; 2. Каждая строка матрицы А [ n ] представляет один и тот же вероятностный вектор
все компоненты которого положительны. Вектор (7.13) в теории ДМЦ занимает особое место из-за наличия многих приложений и называется вектором предельных или финальных вероятностей (иногда - стационарным вектором). Финальные вероятности определяют с помощью векторно-матричного уравнения
которое в развернутом виде будет выглядеть так:
К уравнениям (7.14а) можно дополнительно добавить условие нормировки:
Тогда любое из уравнений в (7.15) можно исключить. Также как и в случае поглощения ДМЦ многие характеристики эргодических цепей определяются с помощью фундаментальной матрицы, которая в этом случае будет иметь вид:
Для эргодических цепей характеристикой, имеющей важное практическое значение, является продолжительность времени, за которое процесс из состояния Si впервые попадает в Sj, так называемое время первого достижения. Матрица средних времен достижения определяется по формуле:
где Mz - фундаментальная матрица (12); Mzdg - диагональная матрица, образованная из фундаментальной, заменой всех элементов, кроме диагональных - нулями; D - диагональная матрица с диагональными элементами dij = 1/a i; Е - матрица, все элементы которой равны единице. Матрица дисперсий времени первого достижения имеет несколько более сложный вид:
где кроме уже упомянутых обозначений встречается новое - (Мz× Мt) dg, обозначающее диагональную матрицу, полученную из матричного произведения матриц Мz× Мt.
ЛИТЕРАТУРА 1. Макаров И.М. и др. Теория выбора и принятия решений. -М.: Наука, 1982. 2. Медиченко М.П. Методы оптимального планирования и управления,ч.1, МО СССР, 1986. 5. Подиновский В.В. Математическая теория выработки решений в сложных ситуациях. МО СССР, 1981. 6. Ватага А.И., Бережной В.В. Математические методы анализа и синтеза сетей связи. Сборник задач. Часть 1. Ставрополь СВВИУС. 7. Бережной В.В., Ватага А.И. Математические методы анализа и синтеза сетей связи. Часть 2. Ставрополь ФРВИ РВ. 8. Бережной В.В. Математические методы анализа и синтеза сетей связи. Часть 3. Ставрополь ФРВИ РВ. 9. Ватага А.И., Бережной В.В. Малофей О.П. Математические методы анализа и синтеза сетей связи. Сборник задач. Часть 2. Ставрополь ФРВИ РВ, 2000. 10. Соболь И.М. Метод Монте-Карло, -М: Наука, 1985. 12. Моудер Дж. Исследование операций, т.1,2 -М: Мир, 1981.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 1377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.239.195 (0.049 с.) |





 ,
,
 - единичная матрица;
- единичная матрица; - нулевая матрица;
- нулевая матрица; - матрица, описывающая переходы в системе из невозвратного множества состояний в поглощающее множество;
- матрица, описывающая переходы в системе из невозвратного множества состояний в поглощающее множество; - матрица, описывающая внутренние переходы в системе в невозвратном множестве состояний.
- матрица, описывающая внутренние переходы в системе в невозвратном множестве состояний. .
.
 .
.


 .
.


 .
.
 ,
,

 .
.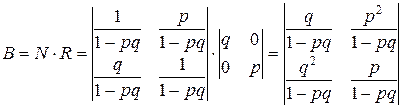 .
.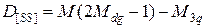 ,
,
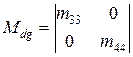 .
.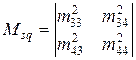 .
. .
.


 .
.
 .
.





