
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачи линейного программированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Впервые общая постановка задачи линейного программирования и один из методов ее решения были сформулированы советским ученым Л.В. Канторовичем в работе «Математические методы организации и планирования производства». Общая математическая теория линейного программирования была разработана в 1949 г. Дж.Данцигом. Дальнейшее развитие теории линейного программирования и ее практических приложений связано с именем отечественных и зарубежных ученых: В.С. Немчинова, В.В. Новожилова, Д.Б. Юдина, Г. Куна, С. Гасса и других. Рассмотрим пример постановки задачи линейного программирования. Для передачи сообщений в автоматизированной системе управления организуется комплекс средств связи. При организации комплекса в распоряжении разработчика имеется n типов средств связи (например, КВ и УКВ радиостанции, средства проводной и радиорелейной связи и т.д.). Комплекс предназначен для работы в различных условиях обстановки (в условиях преднамеренных помех, создаваемых противником, в условиях воздействия различных видов оружия и т.п.). Число различных вариантов обстановки равно m. Каждое из перечисленных средств связи характеризуется показателем эффективности - объемом полезной информации, передаваемой с помощью одного комплекта данного средства за некоторый промежуток времени, который может измеряться в различных единицах. Пусть он измеряется в некоторых условных единицах. Значение в условных единицах показателя эффективности одного комплекта различных типов средств связи, работающих в различных условиях обстановки, представлены в таблице 3.1. Известно, что выполняя задачу управления в i-м варианте обстановки, i =1,..., m, комплекс должен обеспечить передачу сообщений объемом е менее Vi условных единиц. Затраты на эксплуатацию одного комплекта i-го средства связи составляют С, i =1,..., n. Таблица 3.1
Необходимо организовать такой комплекс средств связи, который при минимальных эксплуатационных затратах обеспечил бы выполнение задач управления в любых условиях обстановки.
Проведем формализацию этой задачи. Организовать комплекс, это значит определить количество компонентов каждого типа средств связи, причем таким образом, чтобы затраты на эксплуатацию комплекса были минимальными. Обозначим через x 1 - количество комплектов средств связи первого типа, x 2 - количество комплектов средств связи второго типа и т.д. Тогда в первом варианте обстановки комплекс обеспечит передачу u1 условных единиц информации:
Но по условию задачи управления в первом варианте обстановки необходимо, что u1 ³ V. Следовательно, с учетом (3.1) можно записать
Продолжая аналогичные рассуждения для других вариантов обстановки, приходим к следующей системе неравенств:
Таким образом, система неравенств (3.3) характеризует ограничения на объемы информации, необходимые для выполнения задачи управления в любых условиях обстановки. Эксплуатационные затраты комплекса связи, очевидно, можно записать следующим выражением:
По смыслу задачи величины x 1, x 2 и т.д. не могут принимать отрицательные значения, т.е. имеют место следующие ограничения:
Теперь задачу организации комплекса средств связи можно сформулировать следующим образом: найти такие неотрицательные значения переменных x 1, x 2, x 3,..., xn, которые удовлетворяют ограничениям (3.3) и обращают в минимум целевую функцию (3.4). Так как ограничения представляют систему неравенств, а целевая функция (3.4) - линейную функцию переменных x 1, x 2, x 3,..., xn, то согласно приведенной выше классификации задача организации комплекса средств связи для передачи информации в АСУ относится к задачам линейного программирования.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.195.210 (0.01 с.) |

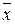 )= С (x 1, x 2,..., xn) = c 1 x 1+ c 2x2+...+ cjxj +...+ cnxn .
)= С (x 1, x 2,..., xn) = c 1 x 1+ c 2x2+...+ cjxj +...+ cnxn .



