
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка и анализ бальных оценокСодержание книги
Поиск на нашем сайте
Пусть перед каждым экспертом была поставлена задача: непосредственно оценить заданные объекты а 1, а 2,..., аn в указанной балльной шкале. Тогда в результате опроса экспертной группы, включающей m членов, будет получена совокупность чисел:
где xij - число баллов, приписанное экспертом i объекту aj. Бальная шкала является промежуточной между порядковой и интервальной. Специальных методов обработки оценок, полученных в подобного рода промежуточных шкалах, пока не создано. Поэтому при обработке бальных оценок поступают следующим образом. Если имеется уверенность, что все эксперты пользуются единой балльной шкалой (одинаково понимают «цену балла»), как это бывает, например, при наличии специальных эталонов, то балльная шкала приближается к интернвалъной, и балльные оценки (6.15) обрабатывают как количественные. В противном случае балльные оценки считают качественными, объекты ранжируют в соответствии с оценками каждого эксперта и затем обрабатывают полученные m ранжировок. Однако и в первом случае целесообразно дважды обработать балльные оценки - как количественные и как качественные. Согласованность результатов, полученных при обоих подходах, будет свидетельствовать о том, что эти результаты действительно основаны на исходных данных, а не на способах их обработки. Будем считать, что оценки (6.15) количественные (а сама балльная шкала непрерывная или же имеет большое число градаций). Тогда, в соответствии с исходным допущением о том, что разница в ответах экспертов объясняется случайными независимыми флюктуациями относительно некоторых «истинных» величин, для обработки данных (6.15) можно использовать обычные статистические методы точечного оценивания. Каждому объекту aj, следует приписать средний балл. Выделение «оригинальных» экспертов на основе их «нестандартных» баллов можно производить известными статистическими методами проверки аномальности результатов, наблюдений.
ГЛАВА 7. МАРКОВСКИЕ МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ Марковские модели принятия решений Общие понятия Любая система может находиться в каждый момент времени t = 0, 1,... в одном из состояний, образующих конечное множество S = {1,..., N }. Говорят, что поведение системы описывается цепью Маркова (однородной) с переходными вероятностями Рij, если через единицу времени после того, как система находилась в состоянии i Î S, с вероятностью Рij она оказывается в состоянии j Î S независимо от того, когда и каким путем она попала в состояние i. Если Рij зависит от момента времени t, в который осуществляется переход, то говорят о неоднородной цепи Маркова. Матрицу P = (Рij) называют матрицей переходов или переходных вероятностей. Управляемой цепью Маркова называется конструкция, задаваемая параметрами < К, Р, r >, где К - решения, Р - вероятности переходов, r - выигрыши. Выигрыш, полученный за несколько шагов, является случайной величиной, зависящей от начального состояния и принимаемых в каждый момент времени решений. Назовем решение, принимаемое в конкретный момент, частным управлением. Тогда управление есть последовательность решений в моменты n =1,2,... Качество управления можно оценить средним суммарным выигрышем (при конечном времени) или среднем выигрышем в единицу времени (при бесконечном времени). Стратегией p называется последовательность решений p = (f 1, f 2, …, fn, …) Другими словами, задание стратегии означает полнее описание в каждый момент времени t =1, 2,..., n,... конкретных решений, которые должны были бы приниматься в i -м состоянии (i = Стратегия (f, f,..., f,...) обозначается через f ¥ и называется стационарной. Стратегия p = (f 1, f 2, …, fn, …) называется марковской, если решение f n принимаемое в каждом конкретном состоянии, не зависит от предшествующих состояний и принимавшихся в них решений. В случае марковской стратегии решения fn могут зависеть только от момента времени n. Свойства оптимальных стратегий: 1. Для бесконечного времени существует оптимальная стационарная стратегия. 2. Для конечного времени существует оптимальная марковская стратегия. Т.о., решение (при бесконечном времени) зависит от состояния, в котором находится система, и не зависит ни от момента времени, ни от всей предыдущей траектории (последовательности состояний и принятых решений). В случае конечного времени оптимальная стратегия является марковской, т.е. может зависеть еще и от момента времени принятия решения. Разберем вычисление среднего выигрыша R (p) на примере. Пусть имеется устройство, которое обслуживается периодически один раз в час. В каждый момент оно может находится в одном из двух состояний: рабочем (состояние 1) и нерабочем (состояние 2). Если устройство на некотором шаге проработало непрерывно 1 час, то доход (выигрыш) равен 3 рублям. При этом вероятность остаться на следующем шаге в состоянии 1 равна 0,7, а вероятность перейти в состояние 2 равна 0,3. Если устройство отказало на некотором шаге, то его можно отремонтировать двумя способами. Первый является ускоренным, требует затрат в 2 рубля (доход равен -2) и обеспечивает переход в состояние 1 с вероятностью 0,6. Второй, обычный способ требует затрат в 1 рубль и обеспечивает переход в состояние 1 с вероятностью 0,4. Определить оптимальный вариант восстановления устройства. В рассматриваемом случае ê К 1 ê= 1, ê К 2 ê= 2, т.е. К 1= {1}, К 1= {1,2}; остальные параметры таковы:
Положим f 1 = <1,1>, f 2 = <1,2> и определим Р (f 1) и Р (f 2)
затем получим r (f 1) = <3, -2>, r (f 2) = <3, -1> Рассмотрим все четыре стратегии длины 2: 2p1=(f 1, f 1), 2p2=(f 1, f 2), 2p3=(f 2, f 1), 2p4=(f 2, f 2) и определим выигрыш для каждой из них. Имеем 2 R (2p1)= Еr (f 1)+ P (f 1) r (f 1)=<3;-2> + 2 R (2p2)= Еr (f 1)+ P (f 1) r (f 2)=<3;-2> + 2 R (2p3)= Еr (f 2)+ P (f 2) r (f 1) = <3;-1> + 2 R (2p4)= Еr (f 2)+ P (f 2) r (f 2)= <3;-1> + Проведенные вычисления показывают, что на конечном времени (до момента 2 включительно) оптимальной является стационарная стратегия (f 2, f 2).
|
||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

 ), если бы система находилась в нем в рассматриваемый момент.
), если бы система находилась в нем в рассматриваемый момент.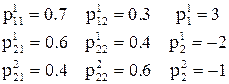
 ;
;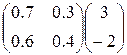 = <3;-2>+<1.5;1>=<4.5;-1>
= <3;-2>+<1.5;1>=<4.5;-1>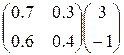 = <3;-2>+<1.8;1.4>=<4.8;-0.6>
= <3;-2>+<1.8;1.4>=<4.8;-0.6>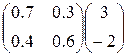 = <3;-1> + <1.5;0> = <4.5;-1>
= <3;-1> + <1.5;0> = <4.5;-1>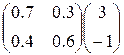 = <3;-1>+<1.8;0.6>=<4.8;-0.4>
= <3;-1>+<1.8;0.6>=<4.8;-0.4>


