
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Допустимое решение в задаче линейного программирования
При решении задачи ЛП табличным симплекс-методом предполагалось, что в начале первого шага известно какое-либо допустимое решение, то есть все базисные переменные положительны. Однако, в общем случае, задача ЛП, приведенная к исходному виду
xn ³ 0 (n = 1, …, k+m) (найти такие xn, которые удовлетворяют (3.23) и обращают в минимум целевую функцию L (x)). Столбец свободных членов наряду с положительными, содержит и отрицательные значения свободных членов b k+i. Это означает, что одна или несколько базисных переменных в начальном решении принимают отрицательные значения, то есть начальное решение не является допустимым, так как оно не удовлетворяет условию неотрицательности переменных x 1, x 2,..., xn. В этом случае необходимо перед применением симплексного метода найти допустимое решение задачи. Изобразим исходную симплекс-таблицу, соответствующую (3.23): Таблица 3.4
Пусть среди свободных членов b k+i есть отрицательные b k+i < 0; 1 ≤ i ≤ m, тогда начальное решение не является допустимым. Заметим в таблице 3.4 строки с отрицательными свободными членами. Если среди них есть строка, в которой кроме свободного члена все остальные элементы неотрицательные, то система (3.23) будет несовместна. Это положение справедливо на всех этапах решения задачи линейного программирования. Допустим, что система (2.23) совместна. Тогда в таблице 3.4, если она содержит отрицательные свободные члены, в соответствующих строках обязательно найдутся отрицательные элементы ν pq < 0. Пусть такой строкой будет s -я строка, где νk+s,l < 0. Вспоминая алгоритм преобразований Жордана, позволяющий получать системы уравнений, равносильные исходной (3.23), можно легко понять, что выбирая элемент νk+s,l в качестве ведущего после осуществления первого жорданова преобразования в s -й строке получим положительный элемент.
Если бы при этом все остальные свободные члены сохранили свои знаки, то общее число отрицательных свободных членов уменьшилась бы на единицу, и, применяя этот шаг последовательно, можно было бы перейти к таблице без отрицательных свободных членов. Однако при выполнении таких шагов в столбце свободных членов новой таблицы количество отрицательных элементов может даже увеличиться, поскольку некоторые свободные члены могут стать отрицательными. Определим условия, при которых обеспечивается последовательное уменьшение количества отрицательных элементов в столбце свободных членов при выполнении преобразования Жордана с ведущим элементом ν k + s,l . Свободные члены, кроме выбранного b k+s, преобразуются в этом случае по формуле
Из выражения (3.26) легко получить условия сохранения в произольной k+i -й строке таблицы (k +1 ≠ k + s) знака свободного члена при выполнении одного преобразования Жордана с ведущим элементом ν k + s,l . В самом деле отношение Рассмотрим отношение 1. При bk+i ³ 0 и νk+i,l < 0 - то есть в круглых скобках выражения (3.26) будет стоять отрицательная величина, а ее произведение на отрицательное ν k + i,l даст в результате b’ k + i > 0. То есть в этом случае свободный член в k+i -й строке новой таблицы останется положительным. 2. При bk+i ³ 0 и νk+i,l > 0 - лишь при условии
то есть элемент ν k + s,l можно выбирать ведущим только тогда, когда он будет знаменателем наименьшего из всех положительных отношений элементов столбца свободных членов к соответствующим элементам ведущего l-го столбца. 3. b k+i < 0. Если при этом νk+i,l > 0, то b’k+i < 0. 4. b k+i < 0. Если при этом νk+i,l < 0, то Однако, приписывая отношению
Сказанное выше можно использовать для последовательного уменьшения числа отрицательных элементов столбца свободных членов симплексной таблицы в случае, если в ней нет нулей и отношение
В самом деле, в этом случае в столбце свободных членов на один отрицательный элемент становится меньше, но, к сожалению, не всегда именно отношение Рассмотрим этот случай, то есть, Поэтому необходимо перейти к новой таблице, взяв в качестве ведущего элемента νk+r,l > 0, для которого отношение В новой таблице число отрицательных свободных членов в этом случае останется тем же самым, что вытекает из анализа (3.26), и элемент b’ k + r сохранит положительный знак. Выполнив конечное число таких преобразований симплекс-таблицы можем иметь лишь два результата: 1) убеждаемся в противоречивости условий задачи; 2) получаем таблицу, которая содержит в некотором столбце отрицательный элемент, который будет знаменателем наименьшего положительного отношения к соответствующему элементу столбца свободных членов, а значит и возможность уменьшения количества отрицательных свободных членов.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.6.75 (0.012 с.) |



 всегда.
всегда.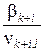 .
. ,
, и b’k+i ³ 0
и b’k+i ³ 0 ³
³  > 0
> 0 знак «+», видим, что оно будет наименьшим среди положительных отношений, а значит, b’k+i новой таблицы только тогда будет равняться нулю, (даже при νk+i,l > 0, когда и bk+i = 0, то есть, когда ведущий элемент взят в строке с нулевым свободным членом. При этом остальные элементы, отличные от нуля, сохраняют, как следует из анализа выражения (3.26), свой знак.
знак «+», видим, что оно будет наименьшим среди положительных отношений, а значит, b’k+i новой таблицы только тогда будет равняться нулю, (даже при νk+i,l > 0, когда и bk+i = 0, то есть, когда ведущий элемент взят в строке с нулевым свободным членом. При этом остальные элементы, отличные от нуля, сохраняют, как следует из анализа выражения (3.26), свой знак. является наименьшим среди всех положительных отношений
является наименьшим среди всех положительных отношений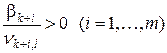
 в l -м столбце. Обычно всегда находится положительный элемент νk+r,l с соответствующим положительным bk+r, для которого справедливо
в l -м столбце. Обычно всегда находится положительный элемент νk+r,l с соответствующим положительным bk+r, для которого справедливо  <
<  , и именно для него отношение
, и именно для него отношение  является минимальным положительным.
является минимальным положительным. , надеясь получить в этой таблице столбец, отрицательный элемент которого будет знаменателем наименьшего положительного отношения, числителем в котором - соответствующий элемент столбца свободных членов.
, надеясь получить в этой таблице столбец, отрицательный элемент которого будет знаменателем наименьшего положительного отношения, числителем в котором - соответствующий элемент столбца свободных членов.


