
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные допущения и уравнения поперечных колебаний прямого стержня.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте При выводе уравнения поперечных колебаний стержня (или балки) мы будем предполагать, что в недеформируемом состоянии так называемая упругая ось стержня прямолинейна и совпадает с линией центров тяжести поперечных сечений стержня. Эту прямолинейную ось мы примем за координатную ось Далее, мы предполагаем, что отклонения точек оси стержня при поперечных колебаниях происходят в одной плоскости (“плоскость колебаний”) и являются “малыми” отклонениями в том смысле, что возникающие при этом восстанавливающие силы остаются в пределах пропорциональности. При таких предположениях отклонения точек оси стержня при поперечных колебаниях однозначно определяются одной функцией двух переменных – координаты
Эта функция удовлетворяет линейному дифференциальному уравнению в частных производных четвертого порядка, которое может быть построено следующим Обозначим через Кинетическая энергия колеблющегося стержня складывается из кинетической энергии поперечных смещений элементов стержня
и кинетической энергии вращения элементов стержня вокруг осей, перпендикулярных к плоскости колебаний,
Потенциальная энергия равна сумме трех слагаемых: а) потенциальной энергии упругой деформации (работа восстанавливающих упругих сил П б) потенциальной энергии прогиба от поперечной нагрузки П в) потенциальной энергии растяжения от продольной силы П Функционал
Уравнение поперечных колебаний стержня мы получим, составив для функционала
где
Это линейное уравнение четвертого порядка, составленное при самых общих предположениях относительно действующих на стержень сил, жесткости и распределения массы. В стержнях, длина которых значительно превосходит поперечные размеры, можно пренебречь инерцией вращения и опустить в левой части уравнения (7) последний член. Положив
где
|
||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 , и от нее будем отсчитывать отклонения элементов стержня при поперечных колебаниях. При этом мы будем считать, по крайней мере на первых порах, что отклонения отдельных точек оси стержня происходят перпендикулярно к прямолинейному, недеформированному ее направлению, пренебрегая смещениями этих точек, параллельными оси.
, и от нее будем отсчитывать отклонения элементов стержня при поперечных колебаниях. При этом мы будем считать, по крайней мере на первых порах, что отклонения отдельных точек оси стержня происходят перпендикулярно к прямолинейному, недеформированному ее направлению, пренебрегая смещениями этих точек, параллельными оси. :
: =
= 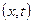
 образом.
образом. массу единицы длины стержня, через
массу единицы длины стержня, через  - жесткость на прогиб (
- жесткость на прогиб ( - модуль упругости,
- модуль упругости,  - момент инерции поперечного сечения стержня относительно нейтральной оси сечения, перпендикулярной к плоскости колебаний),
- момент инерции поперечного сечения стержня относительно нейтральной оси сечения, перпендикулярной к плоскости колебаний),  - момент инерции единицы длины
- момент инерции единицы длины  , а также продольная сила (растягивающая или сжимающая), направленная по оси стержня с интенсивностью
, а также продольная сила (растягивающая или сжимающая), направленная по оси стержня с интенсивностью 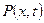 . Эти нагрузки могут зависеть не только от положения элементов стержня, но и от времени.
. Эти нагрузки могут зависеть не только от положения элементов стержня, но и от времени. =
= 
 =
= 
 =
=  (3)
(3) =
= 
 =
=  (5)
(5) Остроградского – Гамильтона имеем здесь вид
Остроградского – Гамильтона имеем здесь вид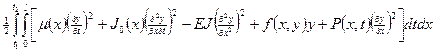 . (6)
. (6) , (*)
, (*) ;
;  ;
;  ;
;  ;
;  .
.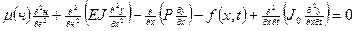 (7)
(7) и
и  , мы рассмотрим сначала свободные колебания однородного стержня с постоянной жесткостью
, мы рассмотрим сначала свободные колебания однородного стержня с постоянной жесткостью  . Для таких колебаний уравнение (7) будет иметь вид
. Для таких колебаний уравнение (7) будет иметь вид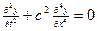 , (8)
, (8) .
.


