
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные формы колебаний стержня и функции, их определяющие.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Простейшим периодическим решением уравнения свободных колебаний стержня
является так называемое главное колебание, в котором
Функция Чтобы получить уравнение собственных форм однородной задачи, подставим (10) в (9). После сокращения на
или
где
Уравнение (11) имеет следующие четыре независимых частных решения:
его общий интеграл
Он содержит четыре произвольные постоянные
пропорциональных соответственно прогибу, углу поворота, изгибающему моменту и перерезывающей силе в точках Во многих отношениях более удобной оказывается следующая система частных решений уравнения (11):
Функции x
Определитель, составленный из этих величин, равен единице. Поэтому функции Крылова называют иногда функциями с единичной матрицей, а систему (14) – нормальной или фундаментальной системой интегралов уравнений (11). Приведем выражения последовательных производных по
(16) Одним из преимуществ функций Крылова является то, что с помощью этих функций можно сразу написать выражение общего интеграла уравнения (11), удовлетворяющего условиям на конце
Колебания стержня со свободными концами (балка, плавающая в жидкости одинаковой с ней плотности; плавающее судно). Краевые в этом случае имеют вид
а интеграл, удовлетворяющий условиям на конце
На конце
откуда
Уравнение частот не отличается от уравнения (22) для стержня с закрепленными концами. Разыскивая периодическое решение уравнения (8) в форме
мы не получим никаких других возможных в данном случае непериодических решений. Между тем очевидно, что уравнению (8) при тех же краевых условиях (23) удовлетворяют функции
Первая определяет поступательное перемещение, одинаковое для всех точек стержня; вторая – вращательное вокруг некоторой оси, положение которой находится из начальных условий. Первая частота колебаний стержня со свободными концами соответствует значению
приведем его к виду
На протяжении от 0 до
ПРОДОЛЬНЫЕ И КРУТИЛЬНЫЕ КОЛЕБАНИЯ ПРЯМЫХ СТЕРЖНЕЙ
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 674; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

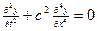 (9)
(9) изменяется с течением времени по гармоническому закону
изменяется с течением времени по гармоническому закону (10)
(10) устанавливающая закон распределения максимальных (амплитудных) отклонений точек оси стержня от равновесного расположения, называется формой главного колебания или собственной формой. Собственных форм колебаний прямого стержня бесконечное множество. Каждой собственной форме соответствует определенное значение частоты
устанавливающая закон распределения максимальных (амплитудных) отклонений точек оси стержня от равновесного расположения, называется формой главного колебания или собственной формой. Собственных форм колебаний прямого стержня бесконечное множество. Каждой собственной форме соответствует определенное значение частоты  - так называемая собственная частота. Отбор собственных частот и соответствующих им собственных форм осуществляется с помощью уравнения собственных форм и краевых условий задачи.
- так называемая собственная частота. Отбор собственных частот и соответствующих им собственных форм осуществляется с помощью уравнения собственных форм и краевых условий задачи. будем иметь
будем иметь
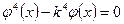 (11)
(11)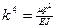 (12)
(12)



 (13)
(13)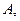


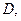 которые должны быть подобраны так, чтобы для функции
которые должны быть подобраны так, чтобы для функции  выполнялись краевые условия, т.е. условия закрепления концов стержня. В обычных случаях, число краевых условий равно числу произвольных постоянных – по два на каждом конце. Все они выражаются равенствами нулю двух из следующих четырех величин:
выполнялись краевые условия, т.е. условия закрепления концов стержня. В обычных случаях, число краевых условий равно числу произвольных постоянных – по два на каждом конце. Все они выражаются равенствами нулю двух из следующих четырех величин:


 или
или  Выполняя эти условия, мы получим четыре однородных уравнения, из которых найдутся отношения постоянных
Выполняя эти условия, мы получим четыре однородных уравнения, из которых найдутся отношения постоянных  и уравнения для определения собственных частот системы.
и уравнения для определения собственных частот системы. (14)
(14) называют функциями А. Н. Крылова. Найдем значение этих функций и их производных по аргументу
называют функциями А. Н. Крылова. Найдем значение этих функций и их производных по аргументу  до третьего порядка включительно при
до третьего порядка включительно при 
 (15)
(15) от функций
от функций  до четвертого порядка включительно.
до четвертого порядка включительно.





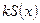













 (23)
(23)

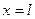

 или
или 


 (24)
(24) Подставив это значение в уравнение форм колебаний
Подставив это значение в уравнение форм колебаний
 .
. функция
функция 



