
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамическое ндс заряда (упругая и вязкоупругая модель).Содержание книги
Поиск на нашем сайте Динамическое состояние заряда: вязкоупругая модель Твердые ракетные топлива обладают ярко выраженными вязкоупругими свойствами. В динамике это проявляется в том, что при нагружении твердотопливного образца синусоидальной деформацией в нем возникает напряжение, сдвинутое по фазе относительно этой деформации. Кроме того, механические свойства зависят от частоты нагружения и температуры образца. Очевидно, эти свойства могут быть перенесены на твердотопливный заряд, поэтому они должны учитываться при расчете его динамического НДС. Частотные характеристики топлива Для оценки динамического состояния заряда используют информацию о механических свойствах топлива при периодическом режиме нагружения /17/. Если, например, в течение опыта на растяжение-сжатие задавать образцу деформацию по закону При этом дополнительно замеряется угол сдвига фаз фе(м).
Рис. 4.1. Динамическое нагружение топливного образца
Если гармонический закон нагружения представить в комплексной форме записи: ε(t) = εa exp(iωt), а реакцию материала в виде 6(t) = ба ехр [i(ωt +φе)], то их отношение будет иметь вид
Полученное выражение не зависит от времени и является комплексным:
гдe
здесь Частотные характеристики топлива зависят от температуры Т, поэтому их определяют при дискретных температурах в заданном диапазоне эксплуатации изделия. Характерные зависимости для динамического модуля
Рис. 4. 2. Частотные зависимости динамического модуля упругости Е* (а) и угла сдвига фаз фЕ (б): 1- Т=-60°С: 2- (-40°С); 3- (-20°С); 4- (0°С); 5-(20°($ 6- (40°С) Видно, что с ростом частоты и понижением температуры динамический модуль Е* возрастает, а тангенс угла сдвига фаз имеет сложный характер изменения и в сильной степени зависит от состава топлива. Еще одной очень важной характеристикой, определяющей жесткость заряда, является коэффициент Пуассона топлива, равный отношению поперечной деформации образца к продольной при его одноосном растяжении. Специальными исследованиями установлено /19/, что при нагружении твердотопливного образца гармонической продольной деформацией коэффициент Пуассона может иметь динамический смысл
На рис.4.3 приведены характерные для твердого топлива зависимости входящих в выражение (4.3) величин для диапазона частот, представляющего интерес при оценке динамического состояния заряда от действия колебаний давления.
Рис.4.3. Частотные зависимости динамического коэффициента Пуассона м* (а) и угла сдвига фаз фц (б): 1- Т=-бО°С; 2- (-40°С); 3- (-20°С); 4- (0°С): 5- (20°С): б- (40°С); 7- (50°С)
Принцип соответствия В отличие от упругой модели, механические свойства топлива в вязко-упругой модели можно описывать комплексными операторами вязкоупругости - модулем f = Re [fE exp(iwt)] (4.4) для каждой зависимой переменной, то решение соответствующей задачи для вязкоупругого материала будет иметь вид
где Выражение "соответствующая задача" означает задачу, в которой упругое тело заменено вязкоупругим. Принцип соответствия применим только при следующих условиях: - решение задачи для упругого материала известно; - при решении задачи для упругого материала не применяется операция, которой при решении задачи для вязкоупругого материала будет соответствовать операция отделения действительной (Re) и мнимой (ш) частей комплексного числа, за исключением окончательного определения f; - граничные условия для двух случаев одинаковы. Решения (3.52) - (3.55) для упругих компонентов НДС заряда соответствуют упругой модели (4.4). Для перевода их в вязкоупругую модель (4.5) необходимо в выражениях (3.52) - (3.55) произвести замену упругих характеристик топлива Еn, Проводить непосредственное преобразование выражений (3.52) - (3.55) по указанной схеме нет необходимости, поскольку операция преобразования комплексных выражений успешно решается вычислительной техникой. Рассмотрим некоторые примеры расчетов. Типичные АЧХ и ФЧХ заряда приведены на рис.4.4, где АЧХ: Дбг - относительное контактное радиальное напряжение, Дбг = Дбг / ДР; Де@ - относительная окружная деформация на канале заряда, Д10 = Дев / ДР; ФЧХ: у%- угол сдвига фаз между колебательными составляющими контактного радиального напряжения и давления в камере двигателя. Из рисунка видно, что основной резонанс системы отчетливо проявляется на АЧХ, в то время как второй резонанс настолько слаб, что его можно идентифицировать лишь с помощью ФЧХ. Это еще раз подтверждает, что при радиальных колебаниях основной интерес представляют частотные характеристики основного тона, где, например, динамические напряжения в несколько раз превышают амплитуду осциллирующего давления в камере двигателя. Обычно резонансные пики на АЧХ весьма узкие, так что при некотором удалении от резонансной частоты уровень динамических напряжений и деформаций быстро уменьшается. Это особенно хорошо видно из рис.4.5, где изображены поля относительных динамических напряжений Д6Г= Дбг / ДР, распределенные по своду заряда. Так, для низкомодульного топлива при частоте 140 Гц и угле сдвига фаз фе = 0,1 рад наибольшие напряжения наблюдаются на контактной поверхности, где они усиливаются по сравнению с амплитудой осциллирующего давления более чем в 15 раз. Однако, если частота колебаний давления окажется на 10 Гц больше, контактные напряжения уменьшатся почти вдвое. Такое усиление динамических напряжений в районе основной резонансной частоты объясняется тем, что на поверхности контакта, кроме упругих, действуют инерционные силы, обусловленные движением заряда. В этом заключается основное отличие распределения динамических напряжений 'по своду заряда от квазистатического при действии постоянного давления (рис.4.5, кривая 1). В районе основной резонансной частоты динамические деформации к оболочке уменьшаются. При частотах, близких ко второй и далее формам радиальных колебаний, максимумы динамических напряжений (так же, как и деформаций) смешаются в тело заряда (550 и 940 Гц). Однако величина их всегда намного меньше, чем в районе основного резонанса. Таким образом, расчетным режимом при оценке динамического НДС заряда следует считать основной резонансный или близкий к нему (при Av -» min), а в качестве расчетных выбираются точки на канале для напряжений и окружной деформации и на контакте для напряжений. Эти точки совпадают с аналогичными точками при статическом анализе /5/. поэтому рассчитанные динамические компоненты НДС могут быть учтены при оценке прочности заряда по формулам, приведением в п.1.4.
0 ZOO WO 6O08Off vT/24 Рис.4.4. АЧХ и ФЧХ вязкоупругого заряда: 1- фе = ОД рад; 2- 0,3 рад
Рис.4.5. Поля относительных динамических напряжений: 1- v=0; 2- 140 Гц; 3- 150 Гц; 4- 550 Гц; 5- 940 Гц
|
||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

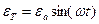 (a - амплитуда деформации), то замеряемое за образцом напряжение будет также меняться гармонически с амплитудой ба, но окажется сдвинутым по фазе на угол фе (рис.4.1), что вызвано вязкоупругой природой топлива:
(a - амплитуда деформации), то замеряемое за образцом напряжение будет также меняться гармонически с амплитудой ба, но окажется сдвинутым по фазе на угол фе (рис.4.1), что вызвано вязкоупругой природой топлива: 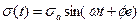 . В этом случае, по аналогии с упругим законом Гука, отношение амплитуд замеряемых величин дает динамический модуль упругости
. В этом случае, по аналогии с упругим законом Гука, отношение амплитуд замеряемых величин дает динамический модуль упругости
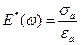 (4.1)
(4.1)

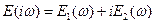


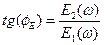
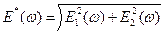
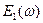 - упругий динамический модуль;
- упругий динамический модуль;  - модуль потерь.
- модуль потерь.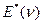 и угла сдвига фаз
и угла сдвига фаз 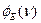 приведены на рис.4.2 /18/.
приведены на рис.4.2 /18/.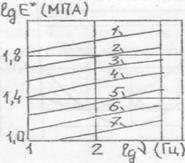

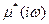 ,т.е. изменяться с частотой нагружения, а между поперечной и продольной деформациями возникает, фазовый сдвиг
,т.е. изменяться с частотой нагружения, а между поперечной и продольной деформациями возникает, фазовый сдвиг 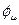 :
: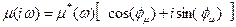 (4.3)
(4.3)

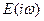 и коэффициентом Пуассона
и коэффициентом Пуассона 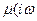 ). Это не единственный способ описания вязкоупругих свойств топлива /17/, но он позволяет наиболее просто получить решение динамической задачи теории линейной вязкоупругости, если известно упругое решение. Для этой цели, при гармоническом нагружении, применяют известный в теории линейной вязкоупругости принцип соответствия /SO/, который формулируется следующим образом: если решение некоторой задачи для упругого материала имеет вид
). Это не единственный способ описания вязкоупругих свойств топлива /17/, но он позволяет наиболее просто получить решение динамической задачи теории линейной вязкоупругости, если известно упругое решение. Для этой цели, при гармоническом нагружении, применяют известный в теории линейной вязкоупругости принцип соответствия /SO/, который формулируется следующим образом: если решение некоторой задачи для упругого материала имеет вид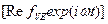 Re
Re  (4.5)
(4.5) обозначает функцию, полученную из функции FЕ заменой упругих постоянных материала на соответствующие комплексные функции.
обозначает функцию, полученную из функции FЕ заменой упругих постоянных материала на соответствующие комплексные функции.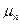 комплексными
комплексными 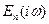 и
и 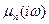 соответственно. Тогда параметры НДС (3.52)-(3.55) также становятся комплексными. После соответствующих алгебраических преобразований по каждой компоненте НДС следует выделить действительную и мнимую часть, после чего определить модуль
соответственно. Тогда параметры НДС (3.52)-(3.55) также становятся комплексными. После соответствующих алгебраических преобразований по каждой компоненте НДС следует выделить действительную и мнимую часть, после чего определить модуль  и аргумент
и аргумент  ) комплексного выражения, т.е. каждое из них представить в виде
) комплексного выражения, т.е. каждое из них представить в виде 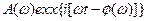 , где А
, где А  - амплитудно-частотная характеристика (АЧХ);
- амплитудно-частотная характеристика (АЧХ); 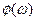 - фазочастотная характеристика (ФЧХ).Знак минус перед ФЧХ обусловлен вязкоупругими свойствами топлива.
- фазочастотная характеристика (ФЧХ).Знак минус перед ФЧХ обусловлен вязкоупругими свойствами топлива.




