
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нелинейные акустические колебанияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1. Использованная выше в линейном анализе гипотеза о бесконечно малой величине возмущений не позволяет рассмотреть развитие действительных возмущений. В линейной теории, как видно, амплитуда возмущений либо вообще не определена (на границе устойчивости), либо растет беспредельно (в зоне неустойчивости), что получается как следствие ее исходных положений. На самом деле при некоторой амплитуде возмущений становятся существенными нелинейные эффекты, которые предотвращают бесконечное увеличение амплитуды и приводят к предельному циклу колебаний. Нелинейность начинает проявляться лишь для возмущений с определенной (критической) амплитудой: при меньшей амплитуде согласно нелинейной теории колебания затухают, при большей - имеет место так называемая нелинейная неустойчивость (неустойчивость в большом, импульсная неустойчивость). Нелинейности колебательного процесса в РДТТ определяются нелинейностью процесса горения и волнового движения в камере, проявляющегося в росте кривизны волн давления, дисперсии возмущений и в возникновении ударных волн. Несмотря на то, что линейные теории обеспечивают довольно полное понимание проблемы неустойчивости РДТТ, они не могут решить чрезвычайно важного для практики вопроса о наиболее опасных для двигателя и для всего ЛА колебаниях большой амплитуды. Поэтому изучению таких нелинейных колебаний уделяется все большее и большее внимание. В настоящее время можно указать узкий круг уже решенных нелинейных задач. 2. Исходные уравнения. Рассмотрим в следующей постановке задачу о нелинейных акустических колебаниях для одномерного течения. Система нелинейных дифференциальных уравнений для такого случая может быть представлена в следующем виде: уравнение сохранения массы газа
уравнение сохранения массы частиц
уравнение сохранения количества движения
уравнение сохранения энергии
где индекс «l» означает массовый расход на единицу длины; v - на единицу объема; остальные индексы и величины прежние. 3. Основные допущения. Для решения этих уравнений сделаем следующие допущения: - отсутствует догорание, т. Е - обмен энергией представлен теплообменом между частицами и газом в КС; - сечение канала заряда неизменно, т. е. F = const; - при z = 0 скорости газа и частиц раины нулю; - для двухфазного потока в сопле предполагается постоянное отставание тяжелой фракции; - режим работы сопла квазистационарный; - характеристики переходного горения определяются функцией чувствительности в виде
следовательно, характеристика горения предполагает линейность; - учитывается связь скорости горения с давлением, в отдельных случаях - со скоростью потока; - частицы рассматривают только одного размера, причем с использованием линейного и нелинейного коэффициента сопротивления. 4. Результаты численного решения. Численные методы решения нелинейных задач устойчивости включают метод характеристик, метод «дискретизации» и др. В последнем случае решение задачи аппроксимируется в предположении удовлетворения нелинейности в конечном числе дискретных точек. Система представленных уравнений (5.84)... (5.87) может решаться, например, методом характеристик. Такое решение, полученное Ф. Куликом, дает зависимость амплитуды возмущений от времени. Примеры результатов численных расчетов Ф. Кулика показаны на рис.7. Начальные условия задавались в виде стоячей волны основной частоты камеры. Начальное возмущение составляло равную часть первой и второй моды, но после трех циклов давление почти не содержало второй гармоники. Влияние связи с переходным горением в этом случае, очевидно, играет решающую роль; функция чувствительности при принятых А и В показывает это в сильной степени для основной частоты и в слабой - для второй моды. Можно отметить также, что амплитуда давления начинает возрастать не сразу; более того наблюдается даже некоторое ее затухание после одного цикла. Это можно объяснить тем, что скорость горения только после нескольких циклов достигает значения, соответствующего возникшим возмущениям давления.
Рис.7. Результаты численных расчетов для основой неустойчивой моды (а, б) и устойчивой второй гармоники (б)(в виде зависимости безразмерной амплиту-ды возмущения давления от безразмерного времени): А = 11,5; В = 0.64; размеры частиц 2 микрона;
|
||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 579; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

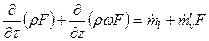 ; (5.84)
; (5.84) ; (5.85)
; (5.85) ; (5.86)
; (5.86) , (5.87)
, (5.87) = 0; Q = 0;
= 0; Q = 0; . (5.88)
. (5.88)
 ;
; 



