
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая модель акустических колебаний в рдттСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1. Общие сведения. Проблема неустойчивости в камере РДТТ включает решение двух вопросов: поведения газа в объеме камеры сгорания и взаимодействия его потока на границе раздела с твердым топливом. Граница раздела фаз включает три элемента: инертную ограничивающую жесткую поверхность, поверхность горения и выходную систему. Каждая из этих границ может быть предметом специального исследования. Для облегчения решения выход (сопло) рассматривают как граничное условие для потока газа из камеры. Для теоретического анализа необходимо выбрать модель процесса (принять упрощающие предпосылки) и записать для каждой из представленных задач дифференциальные уравнения. 2. Основные допущения. Будем считать, что: а) продукты сгорания в камере подчиняются законам идеального газа, в котором отсутствуют силы вязкости, теплообмен со стенками и химические реакции; б) газ является однокомпонентным с постоянной теплопроводностью; в) конденсированные частицы имеют одинаковый размер. Естественно, силы вязкости и теплообмен со стенками могут играть важную роль, но их учет значительно усложняет математическое описание процессов в камере, и поэтому ими пренебрегаем. 3. Исходные уравнения. Поток газа в камере сгорания РДТТ содержит частицы конденсированной фазы. Предполагая, что контрольный объем, для которого записываются исходные уравнения сохранения, содержит кроме газообразных продуктов сгорания и эти конденсированные частицы (причем их объем значительно меньше объема газа), можно обычными методами гидромеханики получить соответствующие уравнения сохранения. Принятые допущения позволяют записать эти уравнения сохранения для потока продуктов сгорания в следующем виде: уравнение сохранения массы (газа)
уравнение сохранения массы (частиц)
уравнение сохранения количества движения
уравнение сохранения энергии
где Комбинируя уравнения (5.53) и (5.55) между собой и переписывая уравнение сохранения количества движения в преобразованном виде можно получить
где
Величина Основным уравнением, используемым в анализе высокочастотной неустойчивости, является нелинейное волновое уравнение для давления, получаемое в результате комбинации уравнения (5.57) с (5.58):
Как видно из записанных уравнении, в частности (5.62) и (5.57), математически задача очень сложна даже с учетом допущений. Для случая одномерного течения система уравнений (5.57) и (5.62) записывается в следующем виде:
Здесь
где Как видно из (5.66), первые два члена в Заметим, если все процессы в камере изоэнтропические, то
Линейный одномерный анализ В любой линейной теории неустойчивости изменение гармонических колебаний во времени изучается с точки зрения того, приводят они к неустойчивости или затухают. Характер переходных процессов в рамках такой теории не исследуется. Вся информация получается путем анализа гармонических колебаний, так как любая функция разлагается на гармонические составляющие. Как известно, в линейной теории рассматриваются колебательные процессы под действием малого начального возмущения. При этом любое возмущение в начальный момент описывается как функция положения в камере сгорания. Для устойчивости необходимо убедиться в затухании всех гармонических составляющих. При анализе же нелинейных эффектов исследовать только гармоническое движение уже недостаточно, так как принцип суперпозиции при этом нарушается. Чтобы найти линейное условие неустойчивости горения, не касаясь вопроса о конечном уровне колебаний, принимают, амплитуду наибольшего возмущения малой. При таком подходе исходные дифференциальные уравнения упрощаются, поскольку величинами второго порядка малости и выше пренебрегают, а анализируются лишь члены, содержащие возмущенные величины в первой степени. Поэтому получаются линейные уравнения относительно возмущений. Линейность возмущений позволяет применить принцип суперпозиции, при котором сумма двух частных решений уравнений также является решением. Поэтому возмущения представляются в виде ряда Фурье, который позволяет анализировать поведение каждого члена ряда в отдельности: при наличии хотя бы одного неустойчивого члена суммарное колебательное движение также будет неустойчивым независимо от поведения остальных членов. Математически это выражается наличием хотя бы одного правого корня в решении характеристического уравнения исходной системы линеаризованных дифференциальных уравнений. При линеаризации исходных уравнений применим несколько отличную по форме от рассматриваемой ранее линеаризации (что одновременно с некоторым упрощением анализа позволяет познакомиться с еще одним методом). Умножим амплитуду каждого возмущения на
где ε — мера амплитуды давления ~ δр/р°; δp(s) — комплексная амплитуда возмущения давления, при которой действительная часть Определяемые таким образом комплексные амплитуды зависят только от координат точки в пространстве. Возмущения скорости можно представить следующим образом:
где μ - мера амплитуды скорости (среднего числа М); Учитывая сказанное, уравнения (5.63) и (5.64) при помощи отношений (5.69) и (5.70) можно привести к следующему виду:
где В силу того, что ε(μ) малы (но не равны нулю), член в фигурных скобках уравнения (5.71), умножаемый на ε, пропадает, так как появляются слагаемые второго порядка малости. Граничные условия записываются для z = 0 и z = L. Уравнения могут быть решены формально для произвольного движения, но это обычно адекватно рассмотрению только гармонического движения. В результате можно получить ответ на вопрос: будут ли начально малые возмущения возрастать или уменьшаться. В линейном анализе, как выше было указано, используется временная зависимость С учетом принятой временной зависимости
при граничных условиях для z = 0 и z = L
Здесь
Знак (^) относится к амплитудам колебаний далеко от стенки. Совместное рас- смотрение уравнений (5.73), (5.74) и следующих:
позволяет окончательно получить выражение для комплексного волнового числа
где Действительная часть выражения (5.80) определяет искомую величину σ:
(5.82) Здесь Слагаемые, входящие в зависимость (5.82), можно интерпретировать следующим образом. Первый член в фигурных скобках представляет связь с поверхностью горения; первое слагаемое в скобках - для конца заряда, второе - для бокового заряда. Второй член в фигурных скобках представляет обмен акустической энергией, который связан с массовым потоком через боковую границу; для прихода массы Первое слагаемое третьей фигурной скобки определяет рассеивание акустической энергии вследствие сил взаимодействия между частицами и газом; второе - потери энергии вследствие приобретения акустической энергии частиц через границу. Последний член (5.82) определяет догорание. Отметим, что полученный результат линейного анализа (5.82), позволяет связать общую акустическую энергию в камере ε и 2 σ:
Аналогичные результаты можно получить для трехмерной задачи с более корректной постановкой задачи (без рассмотренных ранее допущений). Подробнее об этом можно найти в работах Ф. Е. Кулика.
|
||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 ; (5.53)
; (5.53) ; (5.54)
; (5.54) ; (5.55)
; (5.55)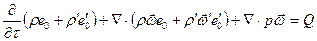 ; (5.56)
; (5.56)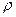 и
и 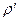 - соответственно плотность газа и конденсированных частиц;
- соответственно плотность газа и конденсированных частиц; 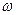 и
и 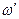 скорость газа и частиц;
скорость газа и частиц; 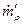 - скорость газообразования в единице объема;
- скорость газообразования в единице объема;  ; Q - скорость тепловыделения в единице объема (скорость выделения энергии в результате гомогенных химических реакций). Здесь и далее одним штрихом обозначены параметры частиц в газе.
; Q - скорость тепловыделения в единице объема (скорость выделения энергии в результате гомогенных химических реакций). Здесь и далее одним штрихом обозначены параметры частиц в газе. ; (5.57)
; (5.57)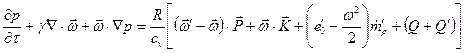 ; (5.58)
; (5.58) - сила взаимодействия между двумя фазами в единице объема:
- сила взаимодействия между двумя фазами в единице объема: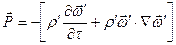 ; (5.59)
; (5.59)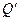 - количество тепла, которым обмениваются между собой газ и частицы:
- количество тепла, которым обмениваются между собой газ и частицы: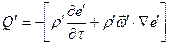 ; (5.60)
; (5.60)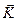 - количество движения, которым обмениваются между собой газ, образующийся со скоростью
- количество движения, которым обмениваются между собой газ, образующийся со скоростью  . (5.61)
. (5.61)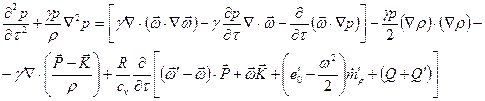 (5.62)
(5.62)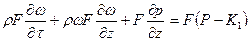 ; (5.63)
; (5.63)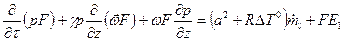 . (5.64)
. (5.64)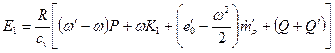 ; (5.65)
; (5.65)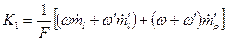 ; (5.66)
; (5.66)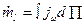 ; (5.67)
; (5.67)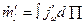 , (5.68)
, (5.68)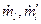 - массовый приход газа и частиц на единицу длины;
- массовый приход газа и частиц на единицу длины;  - массовый приход газа и частиц с единицы поверхностного горения; П - периметр поперечного сечения камеры; F - площадь поперечного сечения;
- массовый приход газа и частиц с единицы поверхностного горения; П - периметр поперечного сечения камеры; F - площадь поперечного сечения; 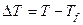 - разница между температурой газа в камере и газом, поступающим из зоны горения,
- разница между температурой газа в камере и газом, поступающим из зоны горения, характеризуют обмен количеством движения между продуктами сгорания в камере и газом, который входит (или выходит) через границы.
характеризуют обмен количеством движения между продуктами сгорания в камере и газом, который входит (или выходит) через границы. представляет собой уменьшение температуры, связанное с неизоэнтропичностью.
представляет собой уменьшение температуры, связанное с неизоэнтропичностью. , где
, где 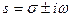 (σ - коэффициент усиления, ω — угловая частота), а возмущение зададим в такой форме:
(σ - коэффициент усиления, ω — угловая частота), а возмущение зададим в такой форме:  ;
; , (5.69)
, (5.69)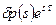 представляет собой действительное мгновенное возмущение (аналогично для плотности).
представляет собой действительное мгновенное возмущение (аналогично для плотности). , (5.70)
, (5.70)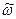 - среднее значение скорости.
- среднее значение скорости.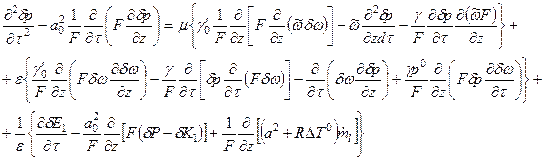 (5.71)
(5.71) , (5.72)
, (5.72)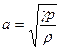 - скорость звука в газе.
- скорость звука в газе.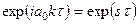 для всех возмущений. Комплексное волновое число k, в котором действительная часть определяет угловую частоту, а мнимая— рост или уменьшение σ, равно:
для всех возмущений. Комплексное волновое число k, в котором действительная часть определяет угловую частоту, а мнимая— рост или уменьшение σ, равно: 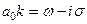 . При σ<0 имеем линейную устойчивость колебаний.
. При σ<0 имеем линейную устойчивость колебаний.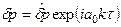 ; (5.73)
; (5.73)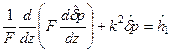 , (5.75)
, (5.75)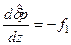 . (5.75)
. (5.75)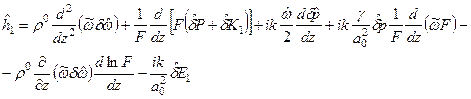 (5.76)
(5.76) . (5.77)
. (5.77)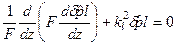 ; (5.78)
; (5.78)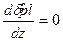 (z =0, L) (5.79)
(z =0, L) (5.79) , (5.80)
, (5.80)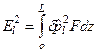 . (5.81)
. (5.81)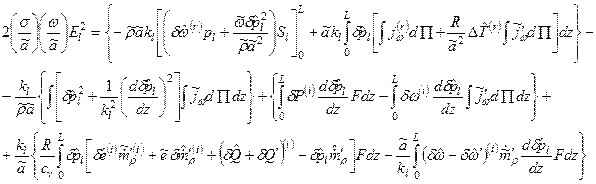
 - приход массы, знак «~» относится к средним величинам.
- приход массы, знак «~» относится к средним величинам.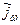 он представляет потери энергии, потому что входящий поток должен приобретать энергию.
он представляет потери энергии, потому что входящий поток должен приобретать энергию. . (5.83)
. (5.83)


