
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Течение жидкости, уравнение неразрывностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
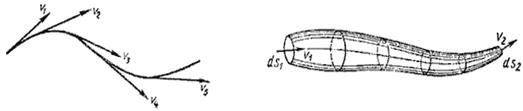
Движение жидкости называется течением, а совокупность частиц движущейся жидкости - потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в данный момент времени (рисунок 9.1). Линии тока проводятся так, чтобы густота их была больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее. Часть жидкости, ограниченная линиями тока, называется трубкой тока.
Рисунок 9.1 – Линия тока и трубка тока
Течение жидкости называется установившимся (или стационарным ), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются. Предположим, что несжимаемая жидкость течет по горизонтальной трубе с переменным сечением (рисунок 9.2). Выделим мысленно несколько сечений в трубе, площади которых обозначим
Рисунок 9.2 – Течение жидкости в трубе переменного сечения Пусть
Так как жидкость несжимаема, то Следовательно,
Другими словами, для несжимаемой жидкости
Уравнение Бернулли
Идеальной жидкостью называется воображаемая жидкость, в которой отсутствуют силы внутреннего трения. В стационарно текущей идеальной жидкости выбираем трубку тока, ограниченную сечениями S1 и S2. По закону сохранения энергии изменение полной энергии жидкости массой m в местах сечений S 1 и S2 равно работе внешних сил по перемещению этой массы жидкости: E2-E 1 =A. Энергия жидкости в двух состояниях:
Работа внешних сил по перемещению массы жидкости:
а силы
Учитывая все это получим
Согласно уравнению непрерывности, объем, занимаемый жидкостью,
Используя выражение m = ρ Δ V, где ρ - плотность жидкости, запишем уравнение Бернулли:
где p – статическое давление (давление жидкости на поверхности обтекаемого тела); ρgh - гидростатическое давление Уравнение Бернулли - выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Из уравнения Бернулли и уравнения неразрывности следует, что при течении жидкости по трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах.
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.72.152 (0.014 с.) |

 и
и  . При стационарном течении через любое поперечное сечение трубы за равные промежутки времени переносятся одинаковые объемы жидкости.
. При стационарном течении через любое поперечное сечение трубы за равные промежутки времени переносятся одинаковые объемы жидкости.
 – скорость жидкости через сечение
– скорость жидкости через сечение 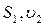 – скорость жидкости через сечение
– скорость жидкости через сечение  объемы жидкостей, протекающих через эти сечения, будут равны:
объемы жидкостей, протекающих через эти сечения, будут равны:

 .
. . (9.5)
. (9.5) . Это соотношение называется уравнением неразрывности.
. Это соотношение называется уравнением неразрывности.

 (9.6)
(9.6) где
где 



 .
.
 (9.7)
(9.7) - динамическое давление.
- динамическое давление.


