
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Затухающие и вынужденные колебанияСодержание книги
Поиск на нашем сайте
Затуханием колебаний называют уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебательной системой (например, превращение энергии колебаний в теплоту вследствие трения в механических системах). Затухание нарушает периодичность колебаний, потому они уже не являются периодическим процессом. Если затухание мало, то можно условно пользоваться понятием периода колебаний – Т (на рисунке 7.6 А 0 – начальная амплитуда колебаний).
Рисунок 7.6 – Характеристики затухающих колебаний
Затухающие механические колебания пружинного маятника происходят под действием двух сил: силы упругости
где r – коэффициент сопротивления. Воспользовавшись уравнением второго закона Ньютона, можно получить:
Разделим последнее уравнение на m и введем обозначение
где β коэффициент затухания, тогда уравнение примет вид
Данное выражение и есть дифференциальное уравнение затухающих колебаний. Решением этого уравнения является
Отсюда следует экспоненциальный характер затухающих колебаний, т.е. амплитуда колебаний убывает по экспоненциальному закону (рисунок 7.6):
Относительное уменьшение амплитуды колебаний за период характеризуется декрементом затухания, равным
или логарифмическим декрементом затухания:
Коэффициент затухания β обратно пропорционален времени τ в течение которого амплитуда колебаний уменьшается в e раз:
Частота затухающих колебаний всегда меньше частоты собственных колебаний и может быть найдена из выражения
где ω0 частота собственных колебаний системы. Соответственно период затухающих колебаний равен:
С увеличением трения период колебаний возрастает, а при Для получения незатухающих колебаний необходимо воздействие дополнительной переменной внешней силы, которая подталкивала бы материальную точку то в одну, то в другую сторону и работа которой непрерывно бы восполняла убыль энергии, затрачиваемой на преодоление трения. Такая переменная сила называется вынуждающей F вын, а возникающие под ее действием незатухающие колебания – вынужденными. Если вынуждающая сила изменяется в соответствием с выражением, то уравнение вынужденных колебаний примет вид
Так как
то
где ωциклическая частота вынуждающей силы. Это дифференциальное уравнение вынужденных колебаний. Решение его может быть записано в виде Уравнение описывает гармоническое колебание, происходящее с частотой, равной частоте вынуждающей силы, отличающееся по фазе на φотносительно колебаний силы. Амплитуда вынужденного колебания:
Разность фаз между колебаниями силы и системы находится из выражения
График вынужденных колебаний приведен на рисунке 7.7.
Рисунок 7.7 – Вынужденные колебания
При вынужденных колебаниях может наблюдаться такое явление, как резонанс. Резонанс это резкое возрастание амплитуды колебаний системы. Определим условие, при котором наступает резонанс, для этого рассмотрим уравнение (7.30). Найдем условие, при котором амплитуда принимает максимальное значение. Из математики известно, что экстремум функции будет, когда производная равна нулю, т.е.
Дискриминант равен
Следовательно
После преобразования получаем Следовательно В простейшем случае резонанс наступает, когда внешняя периодическая сила F меняется с частотой ω, равной частоте собственных колебаний системы ω = ω0.
Механические волны
Процесс распространения колебаний в сплошной среде, периодический во времени и пространстве, называется волновым процессом или волной. При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передается лишь состояние колебательного движения и его энергия. Поэтому основным свойством волн, независимо от их природы, является перенос энергии без переноса вещества. Выделяют следующие типы волн: Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. В любой упругой волне одновременно существуют два вида движения: колебание частиц среды и распространение возмущения. Волна, в которой колебания частиц среды и распространение волны происходят в одном направлении, называется продольной, а волна, в которой частицы среды колеблются перпендикулярно направлению распространения волны, называется поперечной. Продольные волны могут распространяться в средах, в которых возникают упругие силы при деформациях сжатия и растяжения, т.е. твердых, жидких и газообразных телах. Поперечные волны могут распространяться в среде, в которой возникают упругие силы при деформации сдвига, т.е. в твердых телах. Таким образом, в жидкостях и газах возникают только продольные волны, а в твердых телах – как продольные, так и поперечные. Упругая волна называется синусоидальной (или гармонической), если соответствующие ей колебания частиц среды являются гармоническими. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны λ. Длина волны равна расстоянию, на которое распространяется волна за время, равное периоду колебаний:
где Так как Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Бегущими волнами называют волны, которые переносят в пространстве энергию. Для вывода уравнения бегущей волны – зависимости смещения колеблющейся точки от координаты и времени – рассмотрим плоскую синусоидальную волну, распространяющуюся вдоль оси х. Пусть в какой-то точке среды О расположен источник колебаний:
В некоторой точке В, находящейся на расстоянии х от источника, Уравнение колебаний в точке В будет иметь вид
Так как
После подстановки уравнение волны, бегущей вдоль оси х:
В теории волн пользуются понятием волнового вектора:
Абсолютное значение волнового вектора равно числу длин волн на отрезке 2π. Волновой вектор ориентирован в пространстве в направлении распространения волны. В общем случае уравнение бегущей волны, распространяющейся в пространстве вдоль оси х, имеет вид
где Фазовая скорость зависит от частоты Волновое уравнение в этом случае имеет вид
Этому уравнению удовлетворяют плоская и сферическая волны.
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.92.64 (0.011 с.) |



 и силы сопротивления:
и силы сопротивления:
 или
или 
 или
или
 (7.20)
(7.20)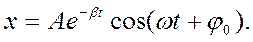 (7.21)
(7.21) (7.22)
(7.22) (7.23)
(7.23)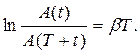 (7.24)
(7.24) т.е.
т.е.  (7.25)
(7.25) (7.26)
(7.26)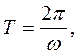 или
или  (7.27)
(7.27) период
период  .
.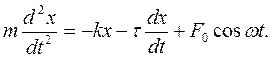 (7.28)
(7.28)
 (7.29)
(7.29)
 (7.30)
(7.30)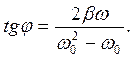 (7.31)
(7.31)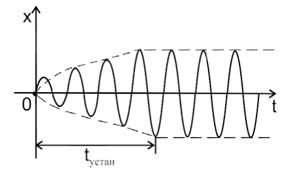

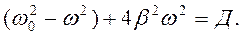
 если
если 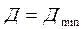
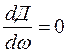 или
или 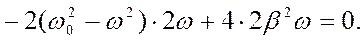

 – резонансная частота.
– резонансная частота.
 – скорость распространения волны.
– скорость распространения волны. (где ν частота колебания), то
(где ν частота колебания), то 

 , где
, где 
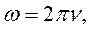 а
а 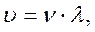 то
то

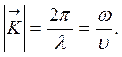 (7.32)
(7.32)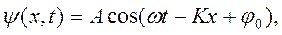 (7.33)
(7.33) волновое число, а фазовая скорость, или скорость распространения волны
волновое число, а фазовая скорость, или скорость распространения волны 


 (7.34)
(7.34)


