
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Второе и третье начало термодинамикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Второе начало термодинамики. Второе начало термодинамики - один из основных законов термодинамики, устанавливающий необратимость макроскопических процессов, протекающих с конечной скоростью. Другими словами, это закон, устанавливающий направление протекания самопроизвольных процессов. Исторически второе начало термодинамики возникло из анализа работы тепловых машин. Существует несколько формулировок второго начала термодинамики. Во-первых, второе начало термодинамики накладывает ограничения на возможности циклического получения механической работы за счёт полученной теплоты (формулировки Клаузиуса и Томсона(Кельвина)). Во-вторых, второе начало термодинамики с помощью понятия энтропии позволяет судить о направлении протекания процессов в системе (формулировка Больцмана). Клаузиус сформулировал второе начало термодинамики следующим образом: теплота не может самопроизвольно перейти от более холодного тела к более нагретому без каких-либо других изменений в системе. В формулировке Томсона (Кельвина) оно звучит как: невозможно преобразовать в работу всю теплоту, взятую от тела с однородной температурой, не производя никаких других изменений в состоянии системы (невозможно создать вечный двигатель второго рода). Следует напомнить, что понятие «вечный двигатель» или «перпетуум-мобиле» появилось где-то в 13 веке и означало воображаемый двигатель, который после запуска совершал бы работу бесконечно долго, не заимствуя энергию извне (вечный двигатель первого рода) [5]. Вечный двигатель первого рода противоречит первому началу термодинамики (закону сохранения и превращения энергии). Наряду с вечным двигателем первого рода рассматривают вечный двигатель второго рода – воображаемую циклическую машину, которая полностью превращала бы в механическую работу теплоту, извлекаемую из окружающих тел (океана, атмосферного воздуха и т.п.). Вечный двигатель второго рода противоречит второму началу термодинамики. Согласно формулировке Больцмана: энтропия изолированной системы при реальных (необратимых) процессах всегда возрастает. Математически эту формулировку можно записать, используя неравенство Клаузиуса в дифференциальном виде:
Второе начало термодинамики имеет статистический смысл. Рост энтропии в изолированной системе означает переход системы в наиболее вероятное, то есть равновесное состояние. Но, принципиально, возможны флуктуации, то есть случайные отклонения физических величин от их средних значений. Количественной мерой флуктуаций может быть дисперсия σх случайной величины Х, а также среднеквадратичное (стандартное) отклонение σх от среднего значения
которая обратно пропорциональна квадратному корню из числа частиц, образующих систему. Флуктуации вызваны беспорядочным тепловым движением частиц, образующих термодинамическую систему, и имеют принципиальное значение, ограничивая пределы применимости термодинамических понятий лишь системами, содержащими большое число частиц, для которых флуктуации много меньше самих флуктуирующих величин. Флуктуации уточняют статистический смысл второго начала термодинамики. Возможны флуктуации системы из равновесного состояния в неравновесное, то есть в определённый промежуток времени система движется в направлении менее вероятных микросостояний. Третье начало термодинамики. С понижением температуры во всякой системе наблюдается тенденция к упорядоченности. Если бы тело можно было охладить до температуры, равной абсолютному нулю, когда тепловые движения молекул не мешали бы установлению порядка, то в системе установился бы идеальный порядок, которому соответствовала бы минимальная энтропия. Если при абсолютном нуле температуры над системой совершить работу, то энтропия системы не изменится. Это доказано и отражено в теореме Нернста: при абсолютном нуле температуры любые изменения состояния происходят без изменения энтропии. При Т=0 энтропия минимальна S=0. Иногда теорему Нернста возводят в ранг третьего начала термодинамики. Часто третье начало термодинамики формулируют так: абсолютный нуль температуры недостижим. Действительно, если бы существовало тело с Т = 0 К (следовательно, S = 0), то можно было бы построить вечный двигатель второго рода, что противоречит второму началу термодинамики. Лекция 14 Элементы физической кинетики
14.1 Понятие о явлениях переноса 14.2 Диффузия в газах 14.3 Вязкость газов 14.4Теплопроводность газов
Понятие о явлениях переноса
Взаимодействие молекул, в частности столкновение между молекулами газа, играет важную роль в процессе установления равновесного состояния. Практически в земных условиях из-за наличия сил сопротивления (сил трения) все системы, в которых не происходит притока энергии извне, являются диссипативными. Если диссипативную систему вывести из состояния равновесия, а затем предоставить самой себе, то она постепенно перейдёт в равновесное состояние. Время, в течение которого система достигает равновесного состояния, называют временем релаксации. Время релаксации различно относительно разных параметров, по которым система может отклоняться от равновесного состояния. Взаимодействия молекул, их столкновения, являются тем механизмом, который приводит систему (газ) в равновесное состояние. В идеальном газе столкновения происходят в основном между парами молекул, одновременным столкновением трёх и более молекул можно пренебречь. Вывести систему, представляющую собой идеальный газ, из равновесного состояния можно, например, нагрев одну часть газа, то есть нарушить тепловое равновесие. Если газ после этого предоставить самому себе, то через некоторое время температура снова станет одинаковой во всех частях газа. Это выравнивание происходит благодаря непрерывному тепловому движению молекул. В нагретой части больше быстрых молекул, имеющих большую тепловую энергию, чем в других частях газа, поэтому быстрые молекулы переходят туда, где их меньше, таким образом, их число становится равным повсюду. Одновременно происходит перемещение молекул и в нагретую область, благодаря соударениям, так что число частиц в единице объёма в среднем не изменяется. Происходит только перенос энергии из той части газа, где она больше, туда, где она меньше. Этот процесс называется теплопроводностью. Если систему вывести из равновесия, добавив примесь другого газа, так, чтобы при одинаковых во всём объёме давлении и температуре, концентрация примеси в одной части была выше, чем во всех других, то спустя определённое время система перейдёт в равновесное состояние за счёт перемещения молекул примеси из области с большей концентрацией в область с меньшей концентрацией. В данном процессе, который называется диффузией, происходит перенос массы примеси. Время релаксации системы в этом случае не равно времени релаксации системы, стремящейся к тепловому равновесию. Равновесие газа может быть нарушено, если одной из его частей сообщена скорость, отличная от скорости течения соседних частей. В этом случае через некоторое время, благодаря переносу импульса упорядоченного движения от более быстрых слоёв к менее быстрым, скорости слоёв выравниваются. Этот процесс называется вязкостью. Все эти процессы можно рассматривать как явления переноса, подходя к их изучению с формальной стороны одинаково: выделяя переносимую величину, выделяя причину переноса, вводя уравнение переноса и времена релаксации. Как уже было отмечено выше, механизм, который приводит систему (газ) в равновесное состояние, обусловлен столкновениями молекул. Основные характеристики молекулярного движения были рассмотрены нами в п. 11.4.
Диффузия в газах Диффузией называется явление взаимного проникновения двух или нескольких соприкасающихся веществ. Каждый из компонентов смеси переходит из области с большей концентрации в область с меньшей концентрацией. При диффузии, таким образом, происходит перенос вещества. Диффузия в газах возникает и в том случае, если они неоднородны по концентрации или плотности (самодиффузия). Для количественного описания этого явления используют понятие диффузионного потока. Диффузионный поток можно выразить через массу переносимого вещества или через число молекул (или молей) переносимого вещества. Диффузионный поток как поток массы определяется массой вещества, перенесённого через площадку dS, перпендикулярную направлению переноса, в единицу времени. Часто используют понятие плотности диффузионного потока. Плотность диффузионного потока определяется массой вещества, перенесённого через единичную площадку, перпендикулярную направлению переноса, в единицу времени. Плотность диффузионного потока равна:
где dM - элемент массы вещества, переносимого через бесконечно малую площадку dS, перпендикулярную направлению переноса, за бесконечно малый промежуток времени dt. Диффузионный поток как поток частиц определяется числом частиц вещества, перенесённого через площадку dS, перпендикулярную направлению переноса, в единицу времени. Плотность диффузионного потока определяется числом частиц вещества, перенесённого через единичную площадку, перпендикулярную направлению переноса, в единицу времени. В этом случае плотность диффузионного потока равна:
где dN - элементарное число частиц вещества, переносимого через бесконечно малую площадку dS, перпендикулярную направлению переноса, за бесконечно малый промежуток времени dt. Основной закон диффузии – закон Фика: плотность диффузионного потока какого-либо компонента вещества прямо пропорциональна градиенту концентрации (плотности) этого компонента со знаком «минус»:
Здесь Градиент плотности можно записать так:
где Для одномерного случая
Аналогично можно записать закон Фика и через поток частиц:
Коэффициент диффузии численно равен плотности диффузионного потока при единичном градиенте концентрации (плотности) и СИ измеряется в В идеальных газах механизм переноса вещества обусловлен соударениями молекул, поэтому, чем выше температура газа, тем больше диффузионный поток и коэффициент диффузии. Коэффициент диффузии, а точнее самодиффузии (диффузии вещества самого в себя, обусловленной неоднородностью концентрации) для идеальных газов можно выразить так:
где Диффузия бывает нестационарной и стационарной. При нестационарной диффузии с течением времени благодаря переносу вещества выравниваются концентрации первоначально неоднородных областей. Разность концентраций со временем убывает по экспоненциальному закону:
Здесь
Стационарная диффузия наблюдается при поддержании постоянным градиента концентрации, и, следовательно, диффузионного потока.
Вязкость газов
Вязкость газов – это свойство, благодаря которому выравниваются скорости упорядоченного движения разных слоёв газа. Можно дать и другое определение. Вязкость газов – это явление переноса, при котором происходит перенос импульса упорядоченного движения от слоёв, движущихся с большей скоростью, к слоям, движущимся с меньшей скоростью. Переносимый импульс можно количественно оценить с помощью потока импульса, равного импульсу упорядоченного движения слоёв, переносимому через площадку dS, параллельную слоям и перпендикулярную к направлению переноса, в единицу времени. Плотность элементарного потока импульса можно записать так:
Основной закон вязкости: плотность потока импульса прямо пропорциональна градиенту скорости со знаком «минус». Знак «минус» показывает, что направление потока импульса противоположно направлению градиента скорости упорядоченного движения.
Здесь
Динамический коэффициент вязкости численно равен потоку импульса при единичном градиенте скорости. В СИ он измеряется в Для идеальных газов коэффициент динамической вязкости можно выразить следующим образом:
Коэффициент вязкости зависит прямо пропорционально от Можно записать основной закон вязкости и через силу вязкого трения, которая направлена по касательной к слоям (к площадке S), используя второй закон Ньютона, согласно которому
Явление вязкости бывает стационарным и нестационарным. О стационарной вязкости говорят, когда градиент скорости поддерживают постоянным. Нестационарная вязкость происходит с изменением градиента, в результате выравниваются скорости взаимодействующих слоёв. Для измерения коэффициента вязкости используют приборы – вискозиметры. Для измерения коэффициента вязкости необходимо, чтобы движение газа было ламинарным, то есть плавным, без завихрений. Этого можно достичь в очень узких трубках – капиллярах. Поэтому такие вискозиметры, в которых используют капилляры, называют капиллярными вискозиметрами.
Теплопроводность газов
Явление возникновения потока тепла в газе (или любом другом веществе) называется теплопроводностью. Перенос количества теплоты можно описать с помощью потока теплоты. Потоком теплоты называется количество теплоты, перенесённое через площадку, перпендикулярную направлению переноса, в единицу времени. Плотность потока теплоты, как количество теплоты, перенесённое через единичную площадку, перпендикулярную направлению переноса, в единицу времени, можно выразить так:
Основной закон теплопроводности – закон Фурье: плотность потока теплоты прямо пропорциональна градиенту температуры со знаком «минус»:
Здесь
Коэффициент теплопроводности численно равен потоку теплоты при единичном градиенте температуры. Для идеальных газов он может быть выражен так:
Здесь СmV – удельная теплоёмкость при постоянном объёме. Коэффициент теплопроводности прямо пропорционален Теплопроводность бывает стационарной, когда градиент температуры поддерживают постоянным, и нестационарной, при которой градиент температуры изменяется. Нестационарная теплопроводность приводит к выравниванию температур разных частей газа. Разность температур со временем убывает по экспоненциальному закону:
Здесь Описанные выше явления переноса имеют много общего с формальной точки зрения. Во-первых, уравнения, выражающие основной закон переноса, формально имеют одинаковый вид. Во-вторых, во всех случаях имеется какая-нибудь переносимая величина, при возникновении градиента некоторых величин. Направление переноса потоков связано с градиентами величин знаком «минус». В. третьих, все рассмотренные явления переноса справедливы при слабом нарушении равновесного состояния системы. Явления переноса в жидкостях и твёрдых телах формально можно описать с помощью аналогичных уравнений переноса. Однако механизм переноса в них отличается от механизма переноса в идеальных газах и выражения коэффициентов переноса невозможны в том же виде, что и для идеальных газов, поскольку для жидкостей и твёрдых тел, где нельзя пренебречь взаимодействием между молекулами, бессмысленно понятие средней длины свободного пробега.
ЛИТЕРАТУРА
1 Савельев И.В. Курс общей физики: В 3 т. – М.: Наука, 1989. 2 Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высш. шк., 1989. – 608 с. 3 Курс физики: Учеб. для вузов: В 2 т. Т.1 / Под ред. В.Н. Лозовского. – СПб.: Издательство «Лань», 2001. – 576 с. 4 Ремизов А.Н., Потапенко А.Я. Курс физики: Учеб. для вузов. – М.: Дрофа, 2002. – 720 с. 5 Трофимова Т.И. Курс физики: Учеб. пособие для вузов. – М.: Высш. шк., 1990. – 478 с. 6 Трофимова Т.И. Краткий курс физики: Учеб. пособие для вузов. – М.: Высш. шк., 2004. – 352 с. 7 Трофимова Т.И., Павлова З.Г. Сборник задач по курсу физики с решениями: Учеб. пособие для вузов. – М.: Высш. шк., 1999. – 591 с. 8 Физический энциклопедический словарь / Гл. ред. А.М. Прохоров. Ред. кол. Д.М. Алексеев, А.М. Бонч-Бруевич, А.С. Боровик-Романов и др. – М.: Сов. энциклопедия, 1984. – 944 с. 9 Енохович А.С. Справочник по физике и технике: Учеб. пособие для учащихся. – М.: Просвещение, 1989. – 224 с. 10 Дмитриева В.Ф. Физика: Учебник для студ. образоват. учреждений сред. проф. Образования. – М.: Издат. центр «Академия», 2003. – 464 с.
|
||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1711; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.014 с.) |


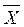 случайной величины или его относительная величина
случайной величины или его относительная величина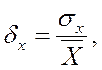
 , (14.1)
, (14.1) , (14.2)
, (14.2) (14.3)
(14.3) - вектор положительной нормали к площадке, через которую переносится вещество; его направление совпадает с направлением переноса вещества. Градиент плотности grad p - это вектор, который, характеризует быстроту изменения скалярной величины – плотности - в пространстве и направлен в сторону наиболее быстрого возрастания данной плотности. D - коэффициент диффузии. Знак «минус» показывает, что направление потока вещества противоположно градиенту плотности.
- вектор положительной нормали к площадке, через которую переносится вещество; его направление совпадает с направлением переноса вещества. Градиент плотности grad p - это вектор, который, характеризует быстроту изменения скалярной величины – плотности - в пространстве и направлен в сторону наиболее быстрого возрастания данной плотности. D - коэффициент диффузии. Знак «минус» показывает, что направление потока вещества противоположно градиенту плотности. , (14.4)
, (14.4) - единичные вектора, направленные вдоль осей x,y,z, соответственно.
- единичные вектора, направленные вдоль осей x,y,z, соответственно. и уравнение (14.3) может быть переписано в скалярном виде при условии, что направления векторов
и уравнение (14.3) может быть переписано в скалярном виде при условии, что направления векторов  и
и  совпадают:
совпадают: (14.5)
(14.5) (14.6)
(14.6) . В системе СГС используют единицу измерения 1 Стокс =
. В системе СГС используют единицу измерения 1 Стокс =  .
.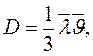 (14.7)
(14.7) - средняя длина свободного пробега молекул идеального газа,
- средняя длина свободного пробега молекул идеального газа,  - средняя арифметическая скорость молекул. При фиксированной температуре
- средняя арифметическая скорость молекул. При фиксированной температуре 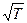 , поэтому коэффициент диффузии в этом случае пропорционален
, поэтому коэффициент диффузии в этом случае пропорционален  .
. (14.8)
(14.8) - время релаксации, то есть время, в течение которого концентрация диффузионного потока уменьшается в е раз; x – расстояние, на котором определяется разность концентраций; S – площадь, через которую происходит диффузия;
- время релаксации, то есть время, в течение которого концентрация диффузионного потока уменьшается в е раз; x – расстояние, на котором определяется разность концентраций; S – площадь, через которую происходит диффузия;  - приведённый объём; V1 – объём области с концентрацией n1; V2 – объём области с концентрацией n2, определяющих разность концентраций
- приведённый объём; V1 – объём области с концентрацией n1; V2 – объём области с концентрацией n2, определяющих разность концентраций .
. (14.9)
(14.9) (14.10)
(14.10) - градиент скорости, направлен в сторону наиболее быстрого возрастания скорости, η- коэффициент динамической вязкости. Для одномерного случая, когда направления векторов
- градиент скорости, направлен в сторону наиболее быстрого возрастания скорости, η- коэффициент динамической вязкости. Для одномерного случая, когда направления векторов  (14.11)
(14.11)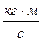 или в Па.с.
или в Па.с.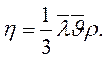 (14.12)
(14.12)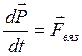 . Для одномерного случая получим:
. Для одномерного случая получим: (14.13)
(14.13) (14.14)
(14.14) (14.15)
(14.15)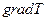 - градиент температуры, направлен в сторону наиболее быстрого возрастания температуры, χ- коэффициент теплопроводности. Для одномерного случая, когда направления векторов
- градиент температуры, направлен в сторону наиболее быстрого возрастания температуры, χ- коэффициент теплопроводности. Для одномерного случая, когда направления векторов  (14.16)
(14.16) (14.17)
(14.17)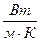 .
. (14.18)
(14.18)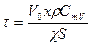 - время релаксации, то есть время, в течение которого между двумя объёмами газа уменьшается в е раз; x – расстояние, на котором определяется разность температур; S – площадь, через которую переносится количество теплоты;
- время релаксации, то есть время, в течение которого между двумя объёмами газа уменьшается в е раз; x – расстояние, на котором определяется разность температур; S – площадь, через которую переносится количество теплоты; 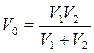 - приведённый объём; V1 – объём области с температурой T1; V2 – объём области с температурой T2, определяющих разность температур
- приведённый объём; V1 – объём области с температурой T1; V2 – объём области с температурой T2, определяющих разность температур 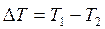 .
.


