
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы сохранения и свойства пространства и времени
Между уравнениями динамики и законами сохранения имеется существенная разница. Законы динамики дают нам представление о детальном ходе процесса. Законы сохранения обусловлены фундаментальными свойствами пространства и времени и поэтому они универсальны и всеобщи. Но они не дают указаний на то, как должен идти тот или иной процесс. Они говорят лишь о том, какие процессы запрещены в природе. Законы сохранения выступают как запреты! Все ниже рассматриваемые законы (законы сохранения импульса и энергии) есть следствие законов движения (например, 2-го закона Ньютона). Поэтому необходимо понимать следующее: законы сохранения можно получить из 2-го закона Ньютона, если к нему присоединить свойства симметрии пространства и времени. Что такое однородность времени, пространства и изотропия пространства? Необходимо дать точные характеристики и определения. Однородность времени означает, что если в два любые момента времени все тела замкнутой системы поставить в совершенно одинаковые условия, то, начиная с этих моментов, все явления в ней будут протекать совершенно одинаково. Однородность пространства означает, что если замкнутую систему тел перенести из одного места пространства в другое, поставив при этом все тела в ней в те же условия, в каких они находились в прежнем положении, то это не отразится на ходе всех последующих явлений. Изотропия пространства означает однородность пространства по отношению к повороту системы на заданный угол. Эти свойства пространства и времени - фундаментальное обобщение опытных фактов. 3.2 Импульс тела, закон сохранения импульса
Импульс тела – векторная физическая величина, равная произведению массы тела на его мгновенную скорость:
Если размерами тела нельзя пренебречь, то это определение имеет смысл только для поступательного движения. Так как масса любого тела положительна, то импульс направлен в ту же сторону, что и его скорость. Единица импульса в системе СИ — 1 кг×м/с. Пусть скорость тела под действием постоянной силы
Ускорение в свою очередь равно:
Подставив (3.3) в (3.2), получим:
Произведение силы на время ее действия называется импульсом силы. Единицей импульса силы —
Формула (3.4) выражает второй закон Ньютона, который может быть сформулирован следующим образом: изменение импульса тела равно импульсу равнодействующей сил, действующих на данное тело. Прежде чем перейти к выводу закона сохранения энергии напомним о понятиях изолированной и неизолированной механических системах Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы (они взаимно уравновешиваются), называется замкнутой или изолированной. В такой системе необходимо учитывать только силы взаимодействия между входящими в нее телами (внутренние силы). Строго говоря, изолированных механических систем в природе не существует. Рассмотрим изолированную механическую систему, состоящую из n тел с массами m1, m2,…, mn. Обозначим скорости этих тел через На основании второго закона Ньютона можно составить следующую систему уравнений движения всех тел системы:
Складывая почленно эти уравнения и группируя силы
Согласно третьему закону Ньютона
Векторная сумма
представляет собой импульс всей системы. Таким образом,
Выражение (3.9) представляет собой закон сохранения импульса: импульс замкнутой системы тел с течением времени не изменяется. Закон сохранения импульса справедлив не только в классической механике; он выполняется и для замкнутых систем микрочастиц, т.е. действует и в квантовой механике. Другими словами, этот закон носит универсальный характер и является фундаментальным законом природы. Закон сохранения импульса позволяет вычислять скорости тел, не зная значения сил, действующих на них и является всеобщим законом: он применим как к телам обычных размеров, так и к космическим телам и элементарным частицам. Очень наглядно и удобно описывать на основе закона сохранения импульса реактивное движение, упругие и неупругие столкновения тел, и другие механические явления происходящие в замкнутых системах.
В классической механике из-за независимости массы от скорости импульс системы можно выразить через скорость ее центра масс. Скорость i -й материальной точки связана с ее радиусом-вектором
Следовательно,
Центром масс или центром инерции системы материальных точек называется воображаемая тоска С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен
где Скорость центра масс определяется выражением:
т.е.
Другими словами, импульс системы равен произведению массы системы на скорость ее центра инерции. Подставив выражение (3.10) в (3.9), получим:
т.е. в изолированной механической системе центр масс находится в покое или движется равномерно и прямолинейно. Если система незамкнутая (на нее действуют помимо внутренних и внешние силы), то выражение (3.9) с учетом (3.10) запишется следующим образом:
или
где Из (3.11) вытекает закон (теорема) движения центра масс: центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 425; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.150.55 (0.009 с.) |
 . (3.1)
. (3.1) изменяется за время
изменяется за время  от
от  до
до  . По второму закону Ньютона
. По второму закону Ньютона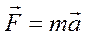 . (3.2)
. (3.2)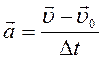 . (3.3)
. (3.3) (3.4)
(3.4) .
. а внутреннюю силу, действующую на i- е тело со стороны k -го, - через
а внутреннюю силу, действующую на i- е тело со стороны k -го, - через  .
. (3.5)
(3.5)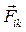 и
и  , получим:
, получим: . (3.6)
. (3.6) = -
= -  , поэтому все скобки в правой части этого уравнения равны нулю, т.е.
, поэтому все скобки в правой части этого уравнения равны нулю, т.е. или
или  . (3.7)
. (3.7)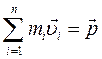 (3.8)
(3.8)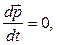 или
или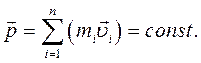 (3.9)
(3.9) соотношением:
соотношением:
 .
.
 масса системы.
масса системы.
 . (3.10)
. (3.10)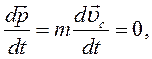
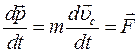 ,
,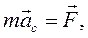 (3.11)
(3.11) ускорение центра масс.
ускорение центра масс.


