
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы Ньютона, фундаментальные взаимодействия
Раздел механики, в котором рассматривается движение тел в связи с вызывающими его причинами (силами), называется динамикой. Основная задача динамики состоит в определении положения тела в произвольный момент времени по известному начальному положению, начальной скорости и силам, действующим на тело. При решении обратной задачи нужно уметь по закону движения тела определять действующие на него неизвестные силы. Основные законы динамики были сформулированы в 80-х годах XVII века И. Ньютоном. В кинематике все системы отсчета равноправны и одинаково допустимы. В динамике следует попытаться выбрать систему отсчета таким образом, что бы рассматриваемые явления выглядели в ней наиболее просто. Существуют такие системы отсчета, относительно которых, всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие других тел не выведет его из этого состояния (первый закон Ньютона):
Иногда первый закон Ньютона называют законом инерции, поскольку явлениесохранения телом скорости движения при отсутствии внешних воздействий называется инерцией. Системы отсчета, в которых тело сохраняет состояние покоя или равномерного прямолинейного движения называются инерционными системами отсчета. Какие же системы отсчета являются инерциальными? Во многих случаях система отсчета, связанная с Землей, — геоцентрическая — может считаться инерциальной. Но строго инерциальной она не является, о чем свидетельствуют опыты с маятником Фуко и с отклонением свободно падающих тел от вертикали. Неинерциальность геоцентрической системы отсчета связана, главным образом с суточным вращением Земли вокруг оси и с орбитальным движением вокруг Солнца. С гораздо большей степенью точности можно считать инерциальной гелиоцентрическую систему отсчета, связанную с Солнцем и неподвижными звездами. Любая система отсчета, которая движется относительно инерциальной с постоянной по величине и направлению скоростью, также является инерциальной. Инерциальной системой отсчета является система отсчета, которая покоится или движется равномерно и прямолинейно относительно некоторой другой инерциальной системы. Законы динамики выполняются только в инерциальных системах отсчета. В какой именно инерциальной системе рассматривается изучаемое механическое движение — совершенно безразлично. Впервые это обстоятельство было осознано Галилеем. Рассматривая механические явления в закрытой каюте корабля, Галилей пришел к выводу, что они происходят одинаково независимо от того, покоится корабль или движется прямолинейно и равномерно. Другими словами, механические явления протекают одинаково во всех инерциальных системах отсчета в том смысле, что описываются одними и теми же законами динамики. Это утверждение о механической эквивалентности всех инерциальных систем отсчета называют принципом относительности Галилея.
Свойство тел сохранять состояние покоя или прямолинейного равномерного движения называется инертностью. Инертность состоит в том, что для изменения скорости тела на заданную величину нужно, чтобы на него действовало другое тело и это действие длилось некоторое время. Инертность — это свойство, присущее всем телам. Опыт показывает, что при одинаковом воздействии различные тела по-разному изменяют свою скорость (приобретают ускорение). Благодаря свойству инертности тело оказывает сопротивление к изменению его скорости. Следовательно, ускорение, приобретаемое телом, зависит не только от величины внешнего воздействия, но и от некоторого собственного свойства тела. Это свойство тела характеризуют физической величиной называемой массой. Масса тела — количественная мера его инертности. О теле, которое в результате взаимодействия меньше изменяет свою скорость, говорят, что оно более инертно. Масса тел определяется путем сравнения с массой некоторого выбранного эталонного тела. По международному соглашению это платина - иридиевый цилиндр, находящийся в Международное бюро мер и весов во Франции и называемый килограммом. Килограмм (кг) является единицей массы тела в системе СИ Воздействие на тело других тел (как причина изменения состояния этого тела) получило общее название силы, действующей на тело. Другими словами. Сила – векторная величина, являющаяся мерой механического действия одного тела на другое.
Ньютон экспериментально установил, что различные силы сообщают одному и тому же телу различные ускорения, а под действием одной и той же силы различные тела по разному изменяют свою скорость. Основываясь на своих опытах он установил следующий закон: ускорение, приобретаемое материальной точкой (телом), прямо пропорционально действующей силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела):
где
Математическим выражением второго закона Ньютона является уравнение:
или
Вектор Таким образом, можно записать:
Выражение (2.5) является более общей формулировкой второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе. Это уравнение называется уравнением движения материальной точки. Единица силы в системе СИ – ньютон (Н): 1 Н – это сила, которая телу массой в 1 кг сообщает ускорение 1 м/с2 в направлении действия силы: 1 Н = 1 кг·1 м/с2. При действии на материальную точку нескольких сил справедлив принцип независимости действия сил: если на материальную точку действуют одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, определяемое вторым законом Ньютона так, как если бы других сил не было:
где сила Таким образом, если на тело действует одновременно несколько сил, то, согласно принципу независимости действия сил, под силой Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго закона: в случае равенства нулю равнодействующей силы ускорение также равно нулю, т.е. тело находится в покое или движется равномерно. Воздействие тел (материальных точек) друг на друга всегда является взаимным и определяется третьим законом Ньютона: действия двух тел друг на друга всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти тела:
где Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками. Современные экспериментальные данные свидетельствуют, что существует только четыре качественно различных вида взаимодействий, в которых участвуют элементарные частицы. Эти взаимодействия называются фундаментальными, то есть самыми основными, исходными, первичными.
Гравитационное взаимодействие. Это взаимодействие носит универсальный характер, в нем участвуют все виды материи, все объекты природы, все элементарные частицы. Гравитация определяет движение планет в звездных системах, играет важную роль в процессах, протекающих в звездах, управляет эволюцией Вселенной, в земных условиях проявляет себя как сила взаимного притяжения. Слабое взаимодействие. Это взаимодействие является наиболее слабым из фундаментальных взаимодействий, экспериментально наблюдаемых в распадах элементарных частиц, где принципиально существенными являются квантовые эффекты. Слабое взаимодействие в отличие от гравитационного является короткодействующим. Экспериментально установлено, что характерный радиус слабого взаимодействия порядка 10-18 м, то есть слабое взаимодействие, сосредоточен на расстояниях меньше размеров атомного ядра. Электромагнитное взаимодействие. В электромагнитном взаимодействии участвуют все заряженные тела, все заряженные элементарные частицы. В этом смысле оно достаточно универсально. Классической теорией электромагнитного взаимодействия является максвелловская электродинамика. В качестве константы связи принимается заряд электрона e. Сильное взаимодействие. Сильное взаимодействие ответственно за устойчивость атомных ядер. Поскольку атомные ядра большинства химических элементов стабильны, то ясно, что взаимодействие, которое удерживает их от распада, должно быть достаточно сильным. Хорошо известно, что ядра состоят из протонов и нейтронов. Чтобы положительно заряженные протоны не разлетелись в разные стороны, необходимо наличие сил притяжения между ними, превосходящих силы электростатического отталкивания. Сильное взаимодействие проявляется на расстояниях прядка 10-15 м и является ответственным за эти силы притяжения.
Силы упругости, закон Гука Перейдем к рассмотрению некоторых конкретных разновидностей сил, широко представленных в природе и технике и играющих важную роль в механических процессах. К ним относятся силы упругости, трения, тяготения и некоторые другие. Начнем с рассмотрения сил упругости. Сила, возникающая в результате деформации тела и направленная в сторону, противоположную перемещениям частиц тела при этой деформации, называется силой упругости.
Деформацией называется изменение формы и размеров тела под воздействием внешней силы или нескольких сил. Различают деформации растяжения (сжатия), изгиба, сдвига, кручения. Деформация тела характеризуется его относительным удлинением ε – отношением изменения длины тела к его первоначальной длине:
где Удлинение тела при действии на него силы связано с возникновением напряжения в теле. Напряжением растяжения или сжатия называется отношение действующей силы (растягивающей или сжимающей) к площади сечения тела, перпендикулярного к направлению силы:
где F – действующая сила, S – площадь сечения, перпендикулярного к направлению силы, Опыт показывает, что если под действием приложенных сил деформация тела (относительное удлинение) не превысит некоторой определенной для каждого материала величины, то тело после прекращения действия деформирующих сил восстанавливает свою первоначальную форму и размеры. Предельная деформация, при которой тело еще сохраняет упругие свойства, называется пределом упругости. Предел упругости задается либо в виде предельного относительного удлинения Если деформация превышает предел упругости, свойственный материалу деформируемого тела, то тело по прекращении действия деформирующих сил не восстанавливает полностью первоначальную форму, остается так называемая «остаточная деформация». Деформация тела за пределом упругости называется пластической, в отличие от упругой деформации, имеющей место в пределах упругости. Тела, имеющие весьма малые пределы упругости (тела из свинца, из мягкой глины, воска и т. д.), называются пластичными; прочие — упругими телами. Зависимость между упругой деформацией и деформирующей силой выражается законом Гука: упругая деформация пропорциональна действующей силе, вызывающей эту деформацию, т. е. пропорциональна напряжению:
где коэффициент Е называется модулем продольной упругости или модулем Юнга. Подставим в формулу (2.10) выражения (2.8) и (2.9). Тогда
Это верно для любых упругих деформаций:
Поскольку, в соответствии с третьим законом Ньютона сила упругости Fуп равна по модулю и противоположна по направлению деформирующей силе F, то можно записать
Теперь закон Гука можно сформулировать в более привычной форме: сила упругости, возникающая при деформации тела, прямо пропорциональна абсолютному удлинению тела и направлена в сторону, противоположную направлению смещения частиц тела. Коэффициент пропорциональности k зависит от упругих свойств материала, его начальной длины и сечения.
Для упругого тела
Когда говорят о пружине или резиновом жгуте, то k называют жесткостью.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 624; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.134.29 (0.026 с.) |
 (2.1)
(2.1)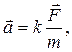 (2.2)
(2.2)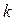 - коэффициент пропорциональности, зависящий от выбора системы единиц. В Международной системе (СИ)
- коэффициент пропорциональности, зависящий от выбора системы единиц. В Международной системе (СИ) 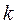 =1, поэтому
=1, поэтому (2.3)
(2.3) (2.4)
(2.4) .
.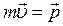 называется импульсом или количеством движения. В отличие от ускорения и скорости, импульс является характеристикой движущегося тела, отражающей не только кинематическую меру движения (скорость), но и его важнейшее динамическое свойство – массу.
называется импульсом или количеством движения. В отличие от ускорения и скорости, импульс является характеристикой движущегося тела, отражающей не только кинематическую меру движения (скорость), но и его важнейшее динамическое свойство – массу.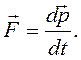 (2.5)
(2.5)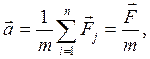 (2.6)
(2.6) называется равнодействующей сил или результирующей силой.
называется равнодействующей сил или результирующей силой.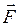 во втором законе Ньютона понимают результирующую силу.
во втором законе Ньютона понимают результирующую силу. (2.7)
(2.7) - сила, действующая на первое тело со стороны второго;
- сила, действующая на первое тело со стороны второго; 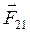 - сила, действующая на второе тело со стороны первого. Необходимо помнить, что силы
- сила, действующая на второе тело со стороны первого. Необходимо помнить, что силы 
 , (2.8)
, (2.8) — удлинение (или укорочение) тела,
— удлинение (или укорочение) тела,  — первоначальная длина.
— первоначальная длина. (2.9)
(2.9) – напряжение.
– напряжение. , при котором материал еще сохраняет упругие свойства, либо (чаще) в виде предельного упругого напряжения
, при котором материал еще сохраняет упругие свойства, либо (чаще) в виде предельного упругого напряжения 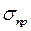 . Каждый материал в данном физическом состоянии, в частности при данной температуре, имеет свой определенный предел упругости.
. Каждый материал в данном физическом состоянии, в частности при данной температуре, имеет свой определенный предел упругости. (2.10)
(2.10) , или
, или  , т.е.
, т.е. 
 . (2.11)
. (2.11) . (2.12)
. (2.12) . (2.13)
. (2.13)


