
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 4 Работа и энергия, закон сохранения энергии
4.1 Работа, энергия и мощность 4.2 Кинетическая энергия 4.3 Консервативные и диссипативные силы 4.4 Закон сохранения энергии в механике
4.1 Работа, энергия и мощность
Энергия — универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других — переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу, равна энергии, полученной последним телом. Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы. Пусть тело движется под действием постоянной сила
где
Рисунок 4.1 – Перемещение тела под действием силы. Работа - скалярная величина. В системе СИ единицей работы является джоуль (Дж). Джоуль равен работе, совершаемой силой 1 Н при перемещении точки ее приложения на 1 м в направлении действия силы: 1 Дж = 1 Н . м. Поскольку работа является скалярной величиной, то она может иметь как положительное, так и отрицательное значение (в зависимости от знака косинуса угла θ). Работа, совершаемая силой При значениях угла 90° < α < 180° работа силы Если вектор силы Рассмотрим работу на конечном пути от точки 1 до точки 2. Разобьем весь путь S от точки 1 до точки 2 на элементарные перемещения, на каждом из которых силу можно считать постоянной. Работа аддитивная величина, т.е. работа на конечном участке пути равна алгебраической сумме работ, совершенных на таких элементарных перемещениях:
Устремив к нулю длины перемещений, а их число - к бесконечности, получим предел суммы, который есть не что иное, как интеграл по траектории:
Итак, работа - криволинейный интеграл вектора
Рисунок 4.2 – Перемещение тела под действием силы. На графике отложена проекция силы на направление движения Для оценки эффективности работы различных механизмов необходимо знать как быстро совершают они ту или иную работу. С этой целью вводится понятие мощности. Мощность N — скалярная физическая величина, равная отношению работы А к промежутку времени
Единица мощности в СИ называется ваттом (Вт). Один ватт равен мощности, при которой совершается работа в 1 Дж за время 1 с В технике пользуются более крупными единицами: киловаттом и мегаваттом. 1 кВт = 103 Вт, 1 МВт = 106 Вт. Работа, совершаемая за 1 ч при мощности в 1 кВт, называется киловатт-часом: 1 кВт . ч = 103 Вт . 3600 с = 3,6 . 106 Дж. В случае движения тела с постоянной скоростью
Любой двигатель или механизм предназначены для выполнения определенной механической работы, которую называют полезной работой Эффективность работы машины характеризуют коэффициентом полезного действия – Коэффициент полезного действия — это отношение полезной работы
где Остановимся теперь более подробно на определении работ, совершаемых силами трения, тяжести и упругости.
Кинетическая энергия
Преобразуем выражение для работы, пользуясь основным уравнением динамики и выражением для пути
Скалярное произведение под интегралом можно представить:
Подставляя (4.8) в (4.7) и рассматривая работу на конечном участке пути от точки 1 до точки 2, получаем:
Из последнего выражение следует, что работа постоянной силы, действующей на тело равна разности энергий в двух состояниях. Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
Таким образом, работа силы при перемещении материальной точки из положения 1 в 2 равна изменению кинетической энергии этой точки
Для системы частиц: кинетическая энергия всей системы материальных точек равна сумме кинетических энергий:
Отметим важный момент: кинетическая энергия определяется работой не только внешних, но и внутренних сил. Этим кинетическая энергия отличается от импульса, который меняется только за счет внешних сил (внутренние силы не меняют импульса всей системы).
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.0.53 (0.007 с.) |
 , которая составляет некоторый угол θ с направлением вектора перемещения. Тогда элементарная работа, совершаемая силой
, которая составляет некоторый угол θ с направлением вектора перемещения. Тогда элементарная работа, совершаемая силой  (4.1)
(4.1)
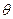 - угол между направлением действующей силы и перемещением (рисунок 4.1).
- угол между направлением действующей силы и перемещением (рисунок 4.1).
 , положительна, если угол θ между вектором силы
, положительна, если угол θ между вектором силы  меньше 90°.
меньше 90°. отрицательна.
отрицательна. . (4.2)
. (4.2) . (4.3)
. (4.3) по траектории S. Графическая иллюстрация понятия работы представлена на рисунке 4.2.
по траектории S. Графическая иллюстрация понятия работы представлена на рисунке 4.2.

 в зависимости от положения частицы на траектории S. Заштрихованная площадка под кривой на расстоянии элементарного перемещения
в зависимости от положения частицы на траектории S. Заштрихованная площадка под кривой на расстоянии элементарного перемещения  равна элементарной работе
равна элементарной работе  . Работа на всем участке 1-2 равна площади под всей кривой от точки 1 до точки 2.
. Работа на всем участке 1-2 равна площади под всей кривой от точки 1 до точки 2. , в течение которого она совершена (скорость совершения работы):
, в течение которого она совершена (скорость совершения работы): . (4.4)
. (4.4) под действием силы F (преодолевающей сопротивление движению) мощность может быть выражена формулой
под действием силы F (преодолевающей сопротивление движению) мощность может быть выражена формулой . (4.5)
. (4.5) .
. (КПД).
(КПД). , совершенной машиной, ко всей затраченной работе
, совершенной машиной, ко всей затраченной работе 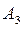 (подведенной энергии
(подведенной энергии  ):
): , (4.6)
, (4.6) — полезная и затраченная мощности соответственно. КПД обычно выражают в процентах.
— полезная и затраченная мощности соответственно. КПД обычно выражают в процентах. :
: . (4.7)
. (4.7) . (4.8)
. (4.8) (4.9)
(4.9) . (4.10)
. (4.10) . (4.11)
. (4.11) (4.12)
(4.12)


