
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В.В. Свиридова, С.В.ШалупаевСодержание книги
Поиск на нашем сайте
В.В. Свиридова, С.В.Шалупаев ФИЗИКА Тексты лекций По разделам «Механика И молекулярная физика» для студентов заочного факультета специальности 1-53 01 02 «Автоматизированные системы обработки информации» Гомель 2014 Содержание
ВВЕДЕНИЕ Физика – наука, изучающая простейшие и вместе с тем наиболее общие закономерности природы, строение и законы движения материи. В условиях непрерывно развивающихся техники и технологий базовые научные знания, на основе которых проектируется любое оборудование и любой технологический процесс, служат защитой от профессиональной дисквалификации. Изучение курса физики способствует развитию у студентов научного мировоззрения, на основе которого складываются представления о современной физической картине мира, формированию умения выделять физическое содержание в прикладных задачах, возникающих в ходе профессиональной деятельности. Структура физики достаточно сложна, хотя на первый взгляд физика состоит из целого ряда независимых разделов – механики, термодинамики, электродинамики, оптики и других. На самом деле эти области физики настолько связаны друг с другом, что не могут существовать друг без друга и, строго говоря, даже не могут быть разделены. При изучении курса физики закладываются основы для изучения общетехнических и специальных дисциплин. Знание физики необходимо для правильного диалектического материалистического представления о явлениях природы. Знание основ механики и молекулярной физики необходимо для решения задач почти всех последующих разделов курса физики, таких, как электростатика, в которой изучаются условия равновесия электрических зарядов (решаются фактически задачи статики), магнетизм, где рассматриваются движения проводников с током в магнитном поле (динамика), движение зарядов в магнитном поле (динамика вращательного движения тела) и т.д. Данный курс лекций подготовлен с учетом практического опыта, накопленного авторами в процессе работы со студентами заочного факультета, что позволило выявить наиболее сложные для понимания слушателями вопросы механики и молекулярной физики и дать краткое и корректное их изложение. Лекции ставят своей целью оказание помощи студентам заочного отделения при подготовке к экзаменам и контрольным мероприятиям. Раздел 1 Механика Лекция 1 Кинематика
1.1 Предмет, задачи и основные понятия механики 1.2 Тангенциальное, нормальное и полное ускорение 1.3 Равномерное движение по окружности 1.4 Неравномерное движение по окружности 1.1 Предмет, задачи и основные понятия механики
В механике рассматриваемые взаимодействия представляют собой те действия тел друг на друга, в результате которых изменяются скорости точек этих тел или возникают деформации, например, притяжения тел по закону всемирного тяготения, взаимные давления соприкасающихся тел, воздействия частиц жидкости или газа друг на друга и на движущиеся в них тела. Под механикой обычно понимают так называемую классическую механику Галилея-Ньютона, предметом изучения которой являются движения любых материальных тел (кроме элементарных частиц), совершаемые со скоростями, малыми по сравнению со скоростью света. Движение макроскопических тел со скоростями порядка скорости света рассматривается релятивистской механикой, основанной на специальной теории относительности Эйнштейна. Для описания движения элементарных частиц и внутриатомных явлений законы классической механики неприменимы – они заменяются законами квантовой механики. Классическая механика делится на три раздела: кинематику, динамику и статику. Кинематика изучает движение тел, не рассматривая причины, которые это движение обусловливают (т.е. движение тел без учета их масс и действующих на них сил). Методы и зависимости, устанавливаемые в кинематике, используются при расчетах передач движения в различных механизмах и машинах, а также при решении задач динамики. Динамика изучает движение материальных тел под действием приложенных к ним сил. В основе динамики лежат законы механики Ньютона, из которых получаются все уравнения и теоремы, необходимые для решения задач динамики. Статика изучает условия равновесия материальных тел под действием сил. Если известны законы движения тел, то из них можно установить и законы равновесия. Поэтому законы статики всегда рассматриваются в связи с законами динамики. Основными понятиями в механике, физике и естествознании в целом являются пространство и время. Всякое материальное тело имеет объем, т.е. пространственную протяженность. Время выражает последовательность состояний материи, составляющих любой процесс, любое движение. Таким образом, пространство и время представляют собой наиболее общие формы существования материи. Любое движение твердого тела можно представить как комбинацию поступательного и вращательного движений. Поступательным движением называют движение, при котором любая прямая, жестко связанная с телом, перемещается, оставаясь параллельной самой себе. Примерами поступательного движения являются движение поршня в цилиндре двигателя, движение кабин «чертова колеса» и т.д. Вращательным движением абсолютно твердого тела называют такое движение, при котором все точки тела движутся в плоскостях, перпендикулярных к неподвижной прямой, называемой осью вращения, и описывают окружности, центры которых лежат на этой оси (роторы турбин, генераторов и двигателей). Как правило, при изучении движения тел их деформации не учитываются, — тела рассматриваются как абсолютно твердые. Абсолютно твердое тело — такое тело, у которого взаимное расположение частиц остается при движении тела неизменным. Часто, рассматривая движение тела, можно пренебречь его размерами и особенностями формы. В таких случаях изучение движения абсолютно твердого тела может быть заменено изучением движения материальной точки. Под материальной точкой понимают тело, размерами которого можно пренебречь в условиях данной задачи. Замена твердого тела материальной точкой представляет собой известную абстракцию (приближение) и может оказаться допустимой при изучении одних движений этого тела и недопустимой при изучении других его движений. Нас будут интересовать два случая, в которых тело можно рассматривать как материальную точку: а) размеры тела малы по сравнению с расстоянием, пройденным телом при его движении, или расстояниями от этого тела до других тел; б) все точки тела движутся одинаково, т. е. имеют в любой момент времени одинаковые скорости и движутся по одинаковым линиям – траекториям. Такое движение тела называется поступательным движением. При таком движении любая прямая, мысленно проведенная в теле, остается параллельной самой себе. Перемещения, мгновенные скорости и ускорения (см. ниже) всех точек одинаковы, т. е. равны по модулю и направлению. Поступательное движение тел можно разделить на два типа по виду траектории движения; прямолинейное движение, если траектория движения – прямая, и криволинейное движение, если траектория — произвольная кривая. Положение тела в пространстве можно определить только относительно какого-нибудь другого тела или других тел. Поэтому, когда речь идет о движений, то имеется в виду относительное движение, т. е. движение тела относительно другого тела, которое условно принимается за неподвижное. Тело отсчета – тело, принимаемое за неподвижное, относительно которого рассматривается движение других тел. Если с телом, принятым за неподвижное и называемым телом отсчета, мысленно связать систему координат, то эта система координат вместе с выбранным способом измерения времени образует систему отсчета. Таким образом, система отсчета состоит из тела отсчета, системы координат, связанной с телом отсчета, и прибора для измерения времени. Обычно пользуются прямоугольной системой координат, представляющей собой совокупность трех взаимно перпендикулярных осей х, у, z. Если движение тела (материальной точки) происходит в одной плоскости, то достаточно двух осей координат х и у (рисунок 1.1).
Рисунок 1.1– К определению понятий система координат, радиус-вектор и координата.
При изучении движения материальной точки ее положение в каждый момент времени определяется по отношению к некоторой системе отсчета координатами материальной точки М либо ее радиус-вектором. Радиус-вектор Координата х точки М – это проекция конца радиуса-вектора точки М на ось ОХ. Основная задача механики - определение положение тела в пространстве в любой момент времени (установить уравнение движения тела). К реальному пространству с высокой степенью точности применима геометрия Евклида, которая наиболее просто выглядит в декартовой системе координат. Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x(t), y = y(t), z = z(t) (координатный способ), либо при помощи зависимости от времени радиус-вектора
Рисунок 1.2 – Векторный и координатный способы описания движения. Путь S – скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: S > 0. Перемещение Δ r тела за определенный промежуток времени — направленный отрезок прямой, соединяющий начальное и конечное положение тела:
где r1 и r2 — радиусы-векторы, определяющие начальное и конечное положения тела. Скорость – мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета. Средняя путевая скорость
Это величина скалярная, по определению не может быть отрицательной, в системе единиц СИ измеряется в метрах на секунду (м/с). Средняя скорость перемещения < < Мгновенная скорость
Здесь
Таким образом, скорость – это векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости
Рисунок 1.3 – Направления средней и мгновенной скоростей. В природе чаще всего наблюдаются движения, в которых скорость изменяется как по величине (модулю), так и по направлению, т.е. приходится иметь дело с неравномерными движениями. Для характеристики изменения скорости таких движений вводится понятие ускорения. Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени. Среднее ускорение — физическая величина, численно равная отношению изменения скорости ко времени, за которое оно произошло: < Мгновенное ускорение:
В зависимости от значений тангенциальной и нормальной составляющих ускорения движение тела классифицируется по-разному. Если Таким образом, движение материальной точки может быть следующих видов: 1) 2) Путь пройденным телом при равномерном движении
При равнопеременном движении
Если начальный момент времени
откуда
Проинтегрировав это выражение в пределах от нуля до произвольного момента времени, получим формулу для нахождения длины пути, пройденного точкой при равнопеременном движении:
Зависимость координаты от времени при равноускоренном прямолинейном движении
Лекция 2 Основы динамики 2.1 Законы Ньютона, фундаментальные взаимодействия Силы упругости, закон Гука 2.3 Силы трения, коэффициент трения 2.4 Гравитационные силы, закон всемирного тяготения. Силы упругости, закон Гука Перейдем к рассмотрению некоторых конкретных разновидностей сил, широко представленных в природе и технике и играющих важную роль в механических процессах. К ним относятся силы упругости, трения, тяготения и некоторые другие. Начнем с рассмотрения сил упругости. Сила, возникающая в результате деформации тела и направленная в сторону, противоположную перемещениям частиц тела при этой деформации, называется силой упругости. Деформацией называется изменение формы и размеров тела под воздействием внешней силы или нескольких сил. Различают деформации растяжения (сжатия), изгиба, сдвига, кручения. Деформация тела характеризуется его относительным удлинением ε – отношением изменения длины тела к его первоначальной длине:
где Удлинение тела при действии на него силы связано с возникновением напряжения в теле. Напряжением растяжения или сжатия называется отношение действующей силы (растягивающей или сжимающей) к площади сечения тела, перпендикулярного к направлению силы:
где F – действующая сила, S – площадь сечения, перпендикулярного к направлению силы, Опыт показывает, что если под действием приложенных сил деформация тела (относительное удлинение) не превысит некоторой определенной для каждого материала величины, то тело после прекращения действия деформирующих сил восстанавливает свою первоначальную форму и размеры. Предельная деформация, при которой тело еще сохраняет упругие свойства, называется пределом упругости. Предел упругости задается либо в виде предельного относительного удлинения Если деформация превышает предел упругости, свойственный материалу деформируемого тела, то тело по прекращении действия деформирующих сил не восстанавливает полностью первоначальную форму, остается так называемая «остаточная деформация». Деформация тела за пределом упругости называется пластической, в отличие от упругой деформации, имеющей место в пределах упругости. Тела, имеющие весьма малые пределы упругости (тела из свинца, из мягкой глины, воска и т. д.), называются пластичными; прочие — упругими телами. Зависимость между упругой деформацией и деформирующей силой выражается законом Гука: упругая деформация пропорциональна действующей силе, вызывающей эту деформацию, т. е. пропорциональна напряжению:
где коэффициент Е называется модулем продольной упругости или модулем Юнга. Подставим в формулу (2.10) выражения (2.8) и (2.9). Тогда
Это верно для любых упругих деформаций:
Поскольку, в соответствии с третьим законом Ньютона сила упругости Fуп равна по модулю и противоположна по направлению деформирующей силе F, то можно записать
Теперь закон Гука можно сформулировать в более привычной форме: сила упругости, возникающая при деформации тела, прямо пропорциональна абсолютному удлинению тела и направлена в сторону, противоположную направлению смещения частиц тела. Коэффициент пропорциональности k зависит от упругих свойств материала, его начальной длины и сечения. Для упругого тела
Когда говорят о пружине или резиновом жгуте, то k называют жесткостью. Формула Циолковского
Применим уравнение (3.12) к движению ракеты, на которую не действуют никакие внешние силы. Тогда, полагая
откуда
или
где С – постоянная интегрирования, определяемая из начальных условий. Если в начальный момент времени
Полученное соотношение называют формулой Циолковского. Из выражения (3.14) следуют следующие практические выводы: а) чем больше конечная масса ракеты m, тем больше должна быть стартовая масса m0; б) чем больше скорость истечения газов u, тем больше может быть конечная масса при данной стартовой массе ракеты. Уравнения Мещерского и Циолковского справедливы для случаев, когда скорости
Кинетическая энергия
Преобразуем выражение для работы, пользуясь основным уравнением динамики и выражением для пути
Скалярное произведение под интегралом можно представить:
Подставляя (4.8) в (4.7) и рассматривая работу на конечном участке пути от точки 1 до точки 2, получаем:
Из последнего выражение следует, что работа постоянной силы, действующей на тело равна разности энергий в двух состояниях. Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
Таким образом, работа силы при перемещении материальной точки из положения 1 в 2 равна изменению кинетической энергии этой точки
Для системы частиц: кинетическая энергия всей системы материальных точек равна сумме кинетических энергий:
Отметим важный момент: кинетическая энергия определяется работой не только внешних, но и внутренних сил. Этим кинетическая энергия отличается от импульса, который меняется только за счет внешних сил (внутренние силы не меняют импульса всей системы). Теорема Штейнера Приведенные выше формулы для моментов инерции тел даны при условии, что ось вращения проходит через центр инерции. Чтобы определить моменты инерции тела относительно произвольной оси, следует воспользоваться теоремой Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции J0 относительно оси, параллельной данной и проходящей через центр инерции тела, и величины md 2:
где m — масса тела, d — расстояние от центра масс до выбранной оси вращения. Единица момента инерции — килограмм-метр в квадрате (кг . м2). Так, момент инерции однородного стержня длиной l относительно оси, проходящей через его конец, по теореме Штейнера равен
Твердого тела Пусть материальная точку массой m, движущуюся по окружности радиусом r под действием постоянной силы F направленная по касательной к окружности. Согласно второму закону Ньютона, эта сила вызывает тангенциальное ускорение
Используя соотношение, связывающее тангенциальное и угловое ускорение ε
получаем
Умножим обе части написанного выше равенства на r:
Левая часть выражения (5.14) является моментом силы: Правая часть представляет собой произведение углового ускорения ε на момент инерции материальной точки А. Так как твердое тело представляет систему неподвижно связанных между собой материальных точек, а для каждой из них справедливо соотношение (5.14), то
Тогда
Обозначая
Угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции. При постоянном моменте вращающей силы угловое ускорение будет величиной постоянной и его можно выразить через разность угловых скоростей:
Тогда основное уравнение динамики вращательного движения можно записать в виде
Эти величины векторные и совпадают по направлению с векторами Определим кинетическую энергию твердого тела, вращающегося вокруг неподвижной оси. Разобьем это тело на n материальных точек. Каждая точка движется с линейной скоростью
Полная кинетическая энергия вращающегося твердого тела равна сумме кинетических энергий всех его материальных точек:
[ J — момент инерции тела относительно оси вращения]. Если тело совершает поступательное и вращательное движения одновременно, то его полная кинетическая энергия равна
Из сопоставления формул кинетической энергии для поступательного и вращательного движений видно, что мерой инертности при вращательном движении служит момент инерции тела. Рассмотрим, например скатывание шара по наклонной плоскости с высоты h без проскальзывания с начальной нулевой скоростью (рисунок 5.4). Найдем скорость перемещения шара в конце спуска. Из закона сохранения энергии
имеем:
Рисунок 5.4 – Скатывание шара с наклонной плоскости.
Условие движения без проскальзывания означает, что линейная скорость центра масс связана с угловой скоростью
Тогда искомая скорость шара в конце спуска:
Центробежные силы инерции
Рассмотрим вращающийся диск с закрепленными на нем стойками с шариками, подвешенными на нитях (рисунок 6.7). При вращении диска с постоянной угловой скоростью
Рисунок 6.7 – К выводу центробежной силы инерции
Согласно второму закону Ньютона
С учетом того, что
т.е. угол отклонения шарика зависит от угловой скорости и от его удаления от оси вращения диска. Относительно неинерциальной системы отсчета, связанной с вращающимся диском, шарик находится в покое. Это возможно в том случае, если сила
Центробежные силы, как и всякие силы инерции, существуют только в ускоренно движущихся (вращающихся) системах отсчета и исчезают при переходе к инерциальным системам отсчета. Действию центробежной силы подвергается, например, пассажир в движущемся автобусе на поворотах. Если в центробежной машине подвесить на нитях несколько шариков и привести машину в быстрое вращение, то центробежные силы инерции отклонят шарики от оси вращения. Угол отклонения тем больше, чем дальше шарик отстоит от оси. Центробежные силы используются в центробежных сушилках для отжима белья, в сепараторах для отделения сливок от молока, в центробежных насосах, центробежных регуляторах и т.д. Их надо учитывать при проектировании быстровращающихся деталей механизмов. Сила Кориолиса
При движении тела относительно вращающейся системы отсчета, кроме центробежной силы, появляется еще одна сила, называемая силой Кориолиса. Рассмотрим шарик массой m, движется прямолинейно со скоростью
Рисунок 6.8 – Действие силы Кориолиса на шарик
Появление силы Кориолиса можно обнаружить, если рассмотреть пример с шариком на спице на вращающемся диске, но без пружины. Для того чтобы заставить шарик двигаться с некоторой скоростью
Если шарик будет перемещаться вдоль спицы с постоянной скоростью
Рисунок 6.9 – К выводу силы Кориолиса
Относительно вращающейся системы (диска) шарик движется с постоянной скоростью. Это можно объяснить тем, что сила Сила
С учетом направления силу Кориолиса
Сила Кориолиса всегда перпендикулярна скорости тела
Механические волны
Процесс распространения колебаний в сплошной среде, периодический во времени и пространстве, называется волновым процессом или волной. При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передается лишь состояние колебательного движения и его энергия. Поэтому основным свойством волн, независимо от их природы, является перенос энергии без переноса вещества. Выделяют следующие типы волн: Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. В любой упругой волне одновременно существуют два вида движения: колебание частиц среды и распространение возмущения. Волна, в которой колебания частиц среды и распространение волны происходят в одном направлении, называется продольной, а волна, в которой частицы среды колеблются перпендикулярно направлению распространения волны, называется поперечной. Продольные волны могут распространяться в средах, в ко
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.7.165 (0.011 с.) |


 точки М – направленный отрезок прямой, соединяющий начало отсчета О с точкой М.
точки М – направленный отрезок прямой, соединяющий начало отсчета О с точкой М.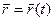 (векторный способ), проведенного из начала координат до данной точки (рисунок 1.2).
(векторный способ), проведенного из начала координат до данной точки (рисунок 1.2).
 , (1.1)
, (1.1)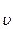 ср – отношение пройденного пути ко времени, за которое этот путь пройден:
ср – отношение пройденного пути ко времени, за которое этот путь пройден: (1.2)
(1.2)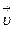 > — векторная физическая величина, равная отношению перемещения
> — векторная физическая величина, равная отношению перемещения  ко времени, за которое это перемещение совершено:
ко времени, за которое это перемещение совершено: (1.3)
(1.3)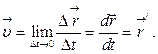 (1.4)
(1.4) (1.5)
(1.5) направлен по касательной к траектории в сторону движения. Различие между средней и мгновенной скоростями показано на рисунке 1.3.
направлен по касательной к траектории в сторону движения. Различие между средней и мгновенной скоростями показано на рисунке 1.3.
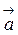 >=
>=  (1.6)
(1.6)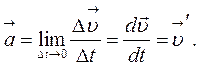 (1.7)
(1.7) (величина скорости не изменяется по величине), движение является равномерным. Если
(величина скорости не изменяется по величине), движение является равномерным. Если  > 0, движение называется ускоренным, если
> 0, движение называется ускоренным, если  0, то движение называется равнопеременным. Наконец, в любом прямолинейном движении
0, то движение называется равнопеременным. Наконец, в любом прямолинейном движении 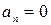 (нет изменения направления скорости).
(нет изменения направления скорости). – прямолинейное равномерное движение.
– прямолинейное равномерное движение. – прямолинейное равнопеременное движение.
– прямолинейное равнопеременное движение. . (1.8)
. (1.8)
 , а начальная скорость
, а начальная скорость 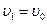 , то, обозначив
, то, обозначив  и
и  , получим:
, получим:
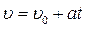 . (1.9)
. (1.9) (1.10)
(1.10) (1.11)
(1.11)
 , (2.8)
, (2.8) — удлинение (или укорочение) тела,
— удлинение (или укорочение) тела,  — первоначальная длина.
— первоначальная длина. (2.9)
(2.9) – напряжение.
– напряжение. , при котором материал еще сохраняет упругие свойства, либо (чаще) в виде предельного упругого напряжения
, при котором материал еще сохраняет упругие свойства, либо (чаще) в виде предельного упругого напряжения 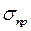 . Каждый материал в данном физическом состоянии, в частности при данной температуре, имеет свой определенный предел упругости.
. Каждый материал в данном физическом состоянии, в частности при данной температуре, имеет свой определенный предел упругости. (2.10)
(2.10) , или
, или  , т.е.
, т.е. 
 . (2.11)
. (2.11) . (2.12)
. (2.12) . (2.13)
. (2.13) и считая, что ракета движется прямолинейно (скорость истечения газов постоянна), получим:
и считая, что ракета движется прямолинейно (скорость истечения газов постоянна), получим: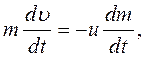
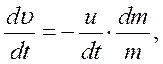

 , а стартовая масса ракеты составляет m0, то
, а стартовая масса ракеты составляет m0, то  .Следовательно,
.Следовательно, (3.14)
(3.14) и
и  намного меньше скорости света с.
намного меньше скорости света с. :
: . (4.7)
. (4.7) . (4.8)
. (4.8) (4.9)
(4.9) . (4.10)
. (4.10) . (4.11)
. (4.11) (4.12)
(4.12) (5.12)
(5.12)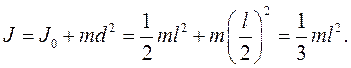 (5.13)
(5.13) или
или 
 ,
,
 (5.14)
(5.14) .
.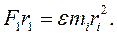

 — суммарный вращающий момент, а
— суммарный вращающий момент, а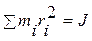 — момент инерции твердого тела относительно оси О'О ', получаем основное уравнение динамики вращательного движения твердого тела:
— момент инерции твердого тела относительно оси О'О ', получаем основное уравнение динамики вращательного движения твердого тела: (5.15)
(5.15) (5.16)
(5.16) или
или  (5.17)
(5.17) — момент импульса (или момент количества движения), М Δ τ — импульс момента сил (или импульс вращающего момента).
— момент импульса (или момент количества движения), М Δ τ — импульс момента сил (или импульс вращающего момента).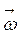 и
и  .
. , тогда кинетическая энергия точки
, тогда кинетическая энергия точки или
или  . (5.18)
. (5.18) (5.19)
(5.19) (5.20)
(5.20)
 .
.
 , момент инерции шара равен
, момент инерции шара равен
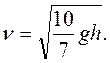
 шарики отклоняются на некоторый угол, тем больший, чем дальше он находится от оси вращения. Относительно инерциальной системы отсчета (неподвижной) все шарики движутся по окружности соответствующего радиуса R, при этом на шарики действует результирующая сила
шарики отклоняются на некоторый угол, тем больший, чем дальше он находится от оси вращения. Относительно инерциальной системы отсчета (неподвижной) все шарики движутся по окружности соответствующего радиуса R, при этом на шарики действует результирующая сила  (рисунок 6.7).
(рисунок 6.7).

 . (6.18)
. (6.18) , можно записать
, можно записать
 (6.18) уравновешена силой инерции
(6.18) уравновешена силой инерции  называемой центробежной силой инерции:
называемой центробежной силой инерции: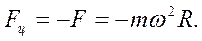 (6.19)
(6.19) от центра к краю диска (рисунок 6.8). Если диск неподвижен, то шарик попадает в точку М, а если диск вращается с постоянной угловой скоростью
от центра к краю диска (рисунок 6.8). Если диск неподвижен, то шарик попадает в точку М, а если диск вращается с постоянной угловой скоростью  , то шарик попадает в точку N. Это обусловлено тем, что на шарик действует сила Кориолиса.
, то шарик попадает в точку N. Это обусловлено тем, что на шарик действует сила Кориолиса.
 (6.20)
(6.20) то с изменением расстояния от центра момент импульса шарика изменится. Для того чтобы заставить шарик двигаться по вращающемуся диску вдоль радиальной прямой со скоростью
то с изменением расстояния от центра момент импульса шарика изменится. Для того чтобы заставить шарик двигаться по вращающемуся диску вдоль радиальной прямой со скоростью 
 уравновешивается приложенной к шарику силой инерции
уравновешивается приложенной к шарику силой инерции  , перпендикулярной к скорости шарика.
, перпендикулярной к скорости шарика. (6.21)
(6.21) (6.22)
(6.22) . Во вращающейся системе отсчета при
. Во вращающейся системе отсчета при  эта сила отсутствует. Таким образом, Кориолисова сила инерции возникает только тогда, когда система отсчета вращается, а тело движется относительно этой системы. Действием силы Кориолиса объясняется ряд эффектов, наблюдающихся на поверхности Земли, например, поворот плоскости колебаний маятника Фуко относительно Земли, отклонение к востоку от линии отвеса свободно падающих тел, размытие правого берега рек в северном полушарии и левого в южном, неодинаковый износ рельсов при двухколейном движении.
эта сила отсутствует. Таким образом, Кориолисова сила инерции возникает только тогда, когда система отсчета вращается, а тело движется относительно этой системы. Действием силы Кориолиса объясняется ряд эффектов, наблюдающихся на поверхности Земли, например, поворот плоскости колебаний маятника Фуко относительно Земли, отклонение к востоку от линии отвеса свободно падающих тел, размытие правого берега рек в северном полушарии и левого в южном, неодинаковый износ рельсов при двухколейном движении.


