Правило знаков. Построение эпюр.

Ранее отмечалось, что при растяжении/сжатии важно различать зоны растяжения и зоны сжатия, так как свойства материалов в них, как правило, различны.

При кручении свойства изотропных материалов не зависят от того в какую сторону скручивается брус – по часовой стрелке или против относительно оси z. Поэтому вводить правило знаков не имеет смысла. Важно только, чтобы при построении эпюр внутренних крутящих моментов разнонаправленные моменты откладывались в разные стороны относительно оси эпюры.

При построении эпюр как и ранее используется метод сечений. Построение эпюр внутренних крутящих моментов полностью аналогично построению эпюр внутренних продольных сил при растяжении сжатии с заменой N(z) на M_к(z).

На рис.7.3 приведен пример построения эпюры внутренних крутящих моментов для бруса, находящегося в опорах, называемых подшипниками.

Такой брус круглого поперечного сечения называется валом.

Подшипники – это опоры, которые не создают противодействия кручению (потери на трение малы и ими можно принебречь). Следовательно, в опорах не возникают опорные реакции – моменты относительно г оси z.

 

I II III IV V VI VII

 

Рисю7.3

 

Запишем уравнения крутящих моментов по участкам:

 

М_к^I = 0;

М_к^II = 200 нм;

М_к^III = 200 нм + 300 нм = 500 нм;

М_к^IV = 200 нм + 300 нм - 600 нм = -100 нм;

М_к^V = 200 нм + 300 нм - 600 нм + 400 нм = 300 нм;

М_к^VI = 200 нм + 300 нм - 600 нм + 400 нм - 500 нм = -200 нм;

М_к^VII = 200 нм + 300 нм - 600 нм + 400 нм - 500 нм + 200 нм = 0

 

При записи уравнений здесь было условно принято, что моменты, вращающие за плоскость чертежа, записываются со знаком «минус», но при построении эпюры эти знаки в поле эпюры не указываются.

 

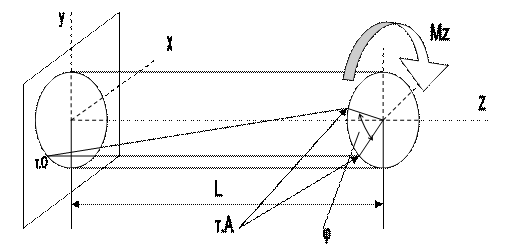
Деформации при кручении.

Рассмотрим деформации при кручении.

Выделим прямую линию ОА, параллельную продольной оси бруса.

Пусть на свободном конце бруса приложен крутящий момент вокруг оси z – М_z. Так как левая точка прямой ОА находится в заделке, то она остается неподвижной, а правая точка А переместится в некоторое новое положение по торцевому поперечному сечению.

При этом угол, который образуется новым и старым положением т.А при соединении этих точек с центром сечения (угол φ) называется абсолютным углом закручивания.

 

 

Рис.7.4

 

Абсолютный угол закручивания измеряется в радианах.

Введем в рассмотрение и относительный угол закручивания θ из соотношения

θ = φ/L. Этот угол измеряется в радианах, отнесенных к единице длины.

Рассмотрим искажение первоначально прямоугольного элемента боковой поверхности вала при кручении (рис.7.5).

 

 

 

 

Рис.7.5

 

Первоначально прямоугольный элемент искажается в параллелограмм. Такое искажение называется «чистым сдвигом», а угол γ – носит название «угол сдвига».

 

Напряжения при кручении.

Рассмотренный выше характер деформированного состояния является следствием действия напряжений, называемых касательными, так как они направлены по касательной к боковой поверхности бруса. Их обычно обозначают τ, и они показаны на следующем рис.7.6.

 

 

Рис.7.6

 

Как отмечалось ранее, расстояния между поперечными сечениями не изменяются, следовательно, можно сделать вывод об отсутствии нормальных напряжений вдоль продольной оси Z.

Учитывая, что касательные напряжения подчиняются «закону парности» (касательные напряжения на взаимно-перпендикулярных гранях равны по величине и направлены в противоположные стороны), окончательно получим, что напряженное состояние при «чистом сдвиге» будет выглядеть следующим образом (рис.7.7):

 

 

Рис.7.7

 

Можно показать, что распределение касательных напряжений по поперечному сечению носит линейный характер (рис.7.8) и они определяются по формуле

 

τ = (M_k ρ)/I_ρ

где: M_k – внутренний крутящий момент в рассматриваемом поперечном сечении;

ρ – расстояние от центра поперечного сечения до произвольной его точки;

Iρ – полярный момент инерции поперечного сечения.

 

Рис.7.8

 

Из этого соотношения можно сделать следующие выводы:

1. касательные напряжения в поперечном сечении изменяются по линейному закону в зависимости от расстояния от центра ρ.

2. в центре тяжести поперечного сечения при ρ=0 касательные напряжения равны 0

3. на боковой поверхности (наиболее удаленные точки поперечного сечения, ρ=D/2) касательные напряжения достигают максимального значения.

Максимальное значение касательных напряжений равно

 

τ_max=(M_k D/2)/I_ρ=M_k/W_ρ,

где W_ρ – полярный момент сопротивления сечения (для круглого поперечного сечения W_ρ = 0,2 D³).