
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные гипотезы и допущения.
Реальные материалы обладают разнообразными физическими свойствами и характерной для каждого из них структурой. С целью упрощения расчетов в сопротивлении материалов используют гипотезы и допущения о свойствах материала. Основные гипотезы и допущения: 1. Материал считается однородным, то есть его свойства во всех точках одинаковы по какому-то направлению. При изменении направления свойства могут измениться, но все равно будут одинаковы во всех точках. 2. Материал считается изотропным, то есть его свойства в произвольной точке одинаковы по всем направлениям. При переходе к другой точке свойства могут измениться, но все равно будут одинаковыми по всем направлениям. 3. Материал считается сплошным, то есть без пустот заполняет пространство, ограниченное поверхностью тела. Таким образом, материал – непрерывен, что позволяет использовать математический аппарат дифференциального и интегрального исчисления. 4. Материал считается идеально упругим, то есть полностью восстанавливает свои форму и размеры после снятия нагрузки. 5. Деформации материала прямо пропорциональны прикладываемым нагрузкам, то есть справедлив закон Гука. 6. Принцип независимости действия сил. При действии на тело нескольких сил, результат действия одной части этих сил не зависит от результата действия остальных сил Следствие: Результат действия на тело нескольких сил равен сумме результатов от действия каждой силы в отдельности и не зависит от последовательности приложения этих сил. Таким образом, одну сложную задачу можно разбить на ряд простых, а результаты «сложить». 7. Принцип начальных размеров. При составлении условий равновесия реального тела оно может считаться абсолютно твердым. То есть деформации тела под нагрузками настолько малы, что можно не учитывать изменение местоположения точек приложения нагрузок и взаиморасположения нагрузок и их линий действия между собой. 8. Гипотеза плоских сечений (Бернулли ) Поперечные сечения тела, бывшие плоскими до нагружения, остаются плоскими и после нагружения. 9. Принцип Сен-Венана. Замена совокупности некоторых сил, приложенных на небольшой части поверхности тела, статически эквивалентной системой других сил не вызовет существенных изменений в условиях нагружения достаточно удаленных частей тела
Рассмотренные выше гипотезы и допущения вносят определенные погрешности в расчеты. Так как «сопротивление материалов» - инженерная наука, то в большинстве случаев этими погрешностями можно пренебречь. Также надо учитывать, что целиком как совокупность указанные предположения используются достаточно редко.
Контрольные вопросы 1. Может ли тело быть «прочным», но не «жестким»? Приведите пример. 2. Приведите пример внешней активной силы и внешней реактивной силы. 3. Приведите пример динамической внешней силы. 4. Из скольких этапов состоит «метод сечений»? 5. Сформулируйте, какими свойствами обладает однородный изотропный материал. 6. Являются ли обычные металлы и сплавы (железо, чугун, сталь и т.д.) «сплошными» материалами? Лекция 4. Центральное растяжение/сжатие прямого бруса
Определение. Примеры. Центральным растяжением/сжатием называется такой вид нагружения бруса, при котором в любом его поперечном сечении возникают только продольные внутренние усилия. П Рис.4.1
Для решения этой задачи применим метод сечений (РОЗУ), состоящий из нескольких этапов. «
«У»- Уравновешиваем неизвестную внутреннюю силу и внешнюю нагрузку -N+500 Н = 0 N = 500 Н Вывод: Внутренняя сила N равна приложенной внешней нагрузке 500 Н. Пример II. А какая сила теперь действует в сечении бруса?
Для решения снова применим метод сечений РОЗУ «Р» -рассекаем брус в интересующем сечении.
«О» -отбрасываем одну из частей бруса.
«З» -для сохранения равновесия заменяем действие отброшенной части бруса на оставшуюся часть бруса неизвестной пока внутренней силой N.
Вывод: внутренняя сила N равна приложенной внешней нагрузке 500 Н Итак: внутренняя продольная сила в рассматриваемом поперечном сечении равна сумме внешних нагрузок в оставшейся после отсечения части бруса.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 835; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.171.121 (0.008 с.) |
 ример I. Какая сила действует в поперечном сечении бруса (рис.4.1)?
ример I. Какая сила действует в поперечном сечении бруса (рис.4.1)? Р» - Рассекаем брус в интересующем нас сечении (рис.4.2)
Р» - Рассекаем брус в интересующем нас сечении (рис.4.2)







 «О» - Отбрасываем одну из частей бруса
«О» - Отбрасываем одну из частей бруса «З»- Для сохранения равновесия заменяем действие отброшенной части на оставшуюся часть бруса неизвестной пока внутренней силой
«З»- Для сохранения равновесия заменяем действие отброшенной части на оставшуюся часть бруса неизвестной пока внутренней силой 

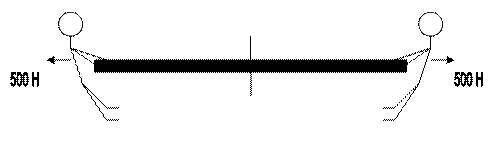

 «У» -уравновешиваем неизвестную внутреннюю силу и внешнюю нагрузку. В итоге получим:
«У» -уравновешиваем неизвестную внутреннюю силу и внешнюю нагрузку. В итоге получим: 



