Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
НИТУ «Московский институт стали и сплавов»Содержание книги
Поиск на нашем сайте НИТУ «Московский институт стали и сплавов» Кафедра теоретической механики и сопротивления материалов А.А.Фролов А.В.Шляков
Механика. Раздел: (разделы «Теоретическая механика/Статика» и «Сопротивление материалов»)
Курс лекций для студентов вечернего факультета (гр. МО, МЦМ, ЭТ, ЭО)
М О С К В А 2010
Оглавление
Введение…………………………………………………………………………………. 4 Лекция 1. Основные понятия статики ……………………………………………….... 5 1.1. Основные определения……………………………………………………… 5 1.2. Аксиома об абсолютно твердом теле. Перенос силы вдоль линии действия. Параллельный перенос силы…………………………… 7 1.3. Линейная система сил……………………………………………………….. 8 1.4. Плоская система сил ………………………………………………………… 8 1.4.1. Система сходящихся сил……………………………………………... 8 1.4.2. Пара сил………………………………………………………………… 9 1.4.3.Произвольная система сил……………………………………………. 9 Лекция 2. Определение опорных реакций (плоский случай)…………………………. 11 2.1. Общие понятия……………………………………………………………….. 11 2.2 Виды опор в плоском случае и их реакции…………………………………. 13 2.3. Алгоритм решения задач по определению опорных реакций…………….. 14 2.4. Примеры……………………………………………………………………….. 14 Лекция 3. Основные определения и понятия сопротивления материалов…………… 17 3.1. Основные определения………………………………………………………. 17 3.2. Понятие о нагрузках. Внешние и внутренние нагрузки. Активные и реактивные нагрузки………………………………………………………. 18 3.3 Метод сечений………………………………………………………………... 19 3.4. Основные гипотезы и допущения…………………………………………. 20 Лекция 4. Центральное растяжение/сжатие прямого бруса…………………………. 22 4.1. Определение. Примеры…………………………………………………….. 22 4.2. Правило знаков продольной силы…………………………………………. 24 4.3. Понятие механических напряжений……………………………………….. 25 4.4. Напряжения в наклонных сечениях. Понятие опасного сечения. Напряжения в опасном сечении……………………………………………. 26 4.5.Построение эпюр продольных сил N(z). Пример………………………….. 27 Лекция 5. Механические свойства материалов. Часть 1……………………………… 29 5.1.1. Измерение деформаций при растяжении/сжатии………………………. 29 5.1.2. Упругие свойства материалов, коэффициент Пуассона μ……………… 30 5.1.3.Упругие свойства материалов, модуль упругости Е…………………….. 31 Лекция 5. Механические свойства материалов. Часть 2……………………………… 33 5.2.1. Виды испытаний и испытательных машин, виды образцов для испытаний …………………………………………………………………. 33 5.2.2. Машинные диаграммы растяжения пластичного образца ……………… 33 5.2.3. Диаграммы условных и истинных напряжений…………………………. 35 5.2.4. Упругая и пластическая (остаточная) составляющие полного удлинения…………………………………………………………………… 36 5.2.5. Механические характеристики материалов………………………………. 36 5.2.6. Пластичные и хрупки материалы…………………………………………. 37 5.2.7. Механические свойства материалов при сжатии………………………… 40 Лекция 6. Понятие допускаемого напряжения. Расчеты на прочность при растяжении/сжатии…………………………………………………………… 41 Лекция 7. Кручение …………………………………………………………………………………….. 44 7.1. Определение. Примеры……………………………………………………… 44 7.2. Правило знаков. Построение эпюр крутящих моментов………………….. 44 7.3. Деформации при кручении………………………………………………….. 45 7.4. Напряжения при кручении…………………………………………………... 46 7.5. Связь между напряжениями и деформациями при кручении. Закон Гука при сдвиге. Условие жесткости……………………………… 48 7.6. Условие прочности при кручении. Виды расчетов на прочность при кручении………………………………………………. 49 Лекция 8. Прямой изгиб………………………………………………………………. 51 8.1. Основные определения…………………………………………………… 51 8.2. Правило знаков Qy, Mx …………………………………………………… 52 8.3. Дифференциальные зависимости между Qy, Mx и q при изгибе……………………………………………… 53 8.4. Пример построения эпюр внутренних силовых факторов при изгибе………………………………………………………………….. 53 Лекция 9. Напряжения при изгибе и расчет на прочность…………………………. 55 9.1.Нормальные напряжения при изгибе……………………………………… 55 9.2. Касательные напряжения при изгибе……………………………………. 58 9.3. Понятие опасного сечения и опасных точек, условие прочности при изгибе……………………………………………………… 59 9.4. Расчет на прочность при изгибе……………………………………………. 60 Лекция 10. Сложное сопротивление…………………………………………………. 62 10.1. Основные понятия…………………………………………………………. 62 10.2. Изгиб в двух плоскостях с кручением……………………………………. 62 10.3. Условие прочности для изгиба с кручением. 4 типа задач на прочность……………………………………………………………….. 63 10.4. Пример расчета ступенчатого вала при действии изгиба с кручением……………………………………………………….. 64 Лекция 11. Циклические напряжения и их влияние на прочность Материалов……………………………………………………………….. 68 11.1. Понятия о циклических напряжениях…………………………………… 68 11.2. Виды циклов, их основные параметры………………………………….. 70 11.3. Явление усталости материалов…………………………………………… 71 11.4. Понятие предела выносливости, его экспериментальное определение………………………………………………………………. 72 11.5. Факторы, влияющие на предел выносливости…………………………. 73 Библиографический список…………………………………………………………… 75 Введение. Реалии учебного процесса для групп МО, МЦМ, ЭО и ЭТ вечернего факультета по курсу «Механика» заключаются в уменьшении количества аудиторных часов при сохранении объемов знаний, которые должны усвоить студенты. Так, в настоящее время общий часовой объем на весь курс составляет всего 72 часа и распределяется по двум семестрам следующим образом: I –й семестр (36 часов) – изучение курсов «Теоретическая механика» (раздел «Статика» и «Сопротивление материалов»); II-ой семестр (36 часов) – изучение курса «Детали машин» и выполнение курсовой работы. Очевидно, что при таких небольших объемах аудиторных занятий (2 часа в неделю) студенты нуждаются в учебных пособиях, в которых достаточно кратко, последовательно и логически взаимосвязано излагались бы основные вопросы перечисленных курсов. При этом необходимо учитывать, что изучение разделов «Статика», «Сопротивления материалов» и «Деталей машин» логически завершается выполнением курсовой работы, где на практике используются полученные теоретические знания. Представляется, что цикл из трех учетных пособий: 1. Избранные лекции по курсу «Механика» (разделы «Статика» и «Сопротивление материалов»); 2. Избранные лекции по курсу «Механика» (раздел «Детали машин») – готовится к изданию; 3. Учебное пособие по выполнению курсовой работы отвечают этим требованиям и окажут помощь в усвоении учебного материала, а также будут полезны при выполнении домашних заданий. Лекция 1. Основные понятия статики 1.1. Основные определения. Материальная точка – тело, пренебрежимо малых размеров. Система материальных точек – совокупность материальных точек, положение которых взаимосвязано, т.е. изменение положения одной из точек приводит к изменению положения остальных точек. Абсолютно твердое тело – система материальных точек, в которой расстояние между двумя произвольными точками не изменяется при действии внешних нагрузок. Мерой механического действия тел друг на друга является сила, которая изображается вектором и характеризуется (рис.1.1): точкой приложения (т. О на рис.1.1), Линейная система сил
Линейной называется такая система сил, в которой все силы действуют по одной прямой, т.е. имеют одну линию действия (рис1.9).
Рис.1.9
Тогда равнодействующая всех этих сил будет равна R=ΣFi, а условие равновесия R=0 или окончательно ΣFi=0 Плоская система сил Плоской называется такая система сил, в которой все силы, а следовательно, и их линии действия лежат в одной плоскости.
Система сходящихся сил
Система сходящихся сил - это такая система сил, в которой линии действия всех сил пересекаются в одной точке – т.е. «сходятся». Так как силы можно переносить вдоль линии действия, то в этом случае все силы имеют одну точку приложения (рис.1.10).
Рис.1.10
Равнодействующая R{Rx,Ry} определяется по правилу параллелограмма (рис.1.11)
Рис.1.11
Тогда, Rx=Σ(Fx)I, Ry=Σ(Fy) i Условие равновесия примет вид R=0, отсюда следует Rx=0, Ry=0 или в проекциях на оси Σ(Fx)i=0, Σ(Fy)i=0. Система пар сил
Это такая система, которая состоит только из пар сил (рис.1.12)
Равнодействующий момент M состоит из алгебраической суммы всех моментов составляющих эту систему с учетом их знаков. Знак момента определяется направлением вращения конкретного момента. Не задавая определенного знака какому либо направлению вращения укажем, что все моменты, вращающие в одну сторону имеют одинаковый знак, а в противоположную сторону- обратный знак. Итак, M = ΣMi = Σ|Fi|hi, где hi – плечо пары сил. Отсюда условие равновесия для системы пар сил будет выглядеть следующим образом:
M = 0 или ΣMi = Σ|Fi|hi = 0. Произвольная система сил. Рис.3.4 Внешние силы Р и R уравновешиваются силами N – внутренними. Внутренние силы начинают действовать только в ответ на действия внешних сил. Они друг друга уравновешивают в каждый момент времени и с течением времени могут изменяться. Внешние нагрузки подразделяются на собственно силы и моменты сил и бывают сосредоточенным (т.е. приложенным в точке) ираспределенными по длине, поверхности (напр., снег на крыше) или объему (например, вес тела). Нагрузки бывают статическими (т.е. практически не изменяющимися во времени) и динамическими (т.е. переменными во времени). Замечание: Статические силы если и изменяются, то столь медленно и плавно, что возникающими при этом ускорениями движущихся масс можно пренебречь. При статическом нагружении можно считать, что нагрузки во всех точках тела воспринимаются одновременно. При динамическом нагружении возникают значительные инерционные силы, которые нужно учитывать наряду с другими нагрузками В сопротивлении материалов изучают действие только уравновешенных систем внешних и внутренних сил. Сосредоточенные силы P измеряются в [Н], [кН], а сосредоточенные моменты M имеют размерность [Нм], [кНм], интенсивность распределенной по линии нагрузки q измеряется в [Н/м], [кН/м], по площади -в [н/м2], [кн/м2], по объему -в [н/м3], [кн/м3]. Метод сечений. Одной из основных задач сопротивления материалов является нахождение внутренних силовых факторов по заданным внешним нагрузкам. Тогда можно судить о прочности, жесткости и устойчивости конструкции. Для этого применяется «метод сечений», который состоит из 4-х этапов. Пусть имеем тело, на которое действуют уравновешенные внешние нагрузки (рис.3.5). Необходимо определить, какие внутренние силы возникают в произвольном поперечном сечении.
Рис.3.5
1. Рассекаем тело в интересующем нас сечении (рис.3.6)
Рис.3.6
2. Отбрасываем одну из частей тела (рис.3.7)
Рис.3.7
3. Заменяем действие отброшенной части на оставшуюся часть неизвестными внутренними силовыми факторами (рис3.8). При этом неизвестные внутренние силовые факторы переводятся во внешние. R –равнодействующая всех неизвестных внутренних сил с двумя проекциями Ry и Rz, а М – суммарный момент всех неизвестных внутренних моментов.
Рис.3.8
4. Составляем уравнения равновесия статики. Получаем систему линейных уравнений с тремя неизвестными Ry, Rz и M, решая которую, находим искомые внутренние силы в поперечном сечении. Начальные буквы этих этапов образуют аббревиатуру «РОЗУ», которая помогает запомнить основные этапы метода сечений. Определение. Примеры. Центральным растяжением/сжатием называется такой вид нагружения бруса, при котором в любом его поперечном сечении возникают только продольные внутренние усилия. П Рис.4.1
Для решения этой задачи применим метод сечений (РОЗУ), состоящий из нескольких этапов. «
«У»- Уравновешиваем неизвестную внутреннюю силу и внешнюю нагрузку -N+500 Н = 0 N = 500 Н Вывод: Внутренняя сила N равна приложенной внешней нагрузке 500 Н. Пример II. А какая сила теперь действует в сечении бруса?
Для решения снова применим метод сечений РОЗУ «Р» -рассекаем брус в интересующем сечении.
«О» -отбрасываем одну из частей бруса.
«З» -для сохранения равновесия заменяем действие отброшенной части бруса на оставшуюся часть бруса неизвестной пока внутренней силой N. Вывод: внутренняя сила N равна приложенной внешней нагрузке 500 Н Итак: внутренняя продольная сила в рассматриваемом поперечном сечении равна сумме внешних нагрузок в оставшейся после отсечения части бруса. Рис.4.4 Вывод: разрушение материала является следствием действия не силы, а другого фактора механического воздействия, а именно – механического напряжения ( отношения внутренней продольной силы к площади поперечного сечения). Механическое напряжение обозначается буквой σ и вычисляется по формуле: σ = N/A где N – внутренняя продольная сила, А – площадь поперечного сечения. Напряжение измеряется в системе «СИ» обычно в Н/м2 [Па] или 106 х Н/м2 [мПа]. В опытах N2, N3 напряжение при разрушении одинаковое и равно:
σ = Nразр./A = P1разр./A Закон Гука. Преобразуем полученное выражение следующим образом:
Δl=Nl0/ЕА
Эту зависимость принято называть первой формулировкой закона Гука [3]. Произведение ЕА называют «жесткостью» материала при растяжении или сжатии, увеличение которой приводит к уменьшению «податливости» материала при нагрузке, т.е. к уменьшению деформаций при прочих равных условиях. Формула закона Гука легко приводится к виду: σ=Е ε
Из формулы закона Гука следует, что размерность модуля Юнга совпадает с размерностью напряжений (т.е. в системе «Си» - [н/м2 =Па]. Формула закона Гука получена при условии постоянства силы N. Если же сила N является переменной (зависит от координаты Z), то указанная формула принимает более сложную «интегральную» форму: Δl=∫(N(z)/EA)dz
Контрольные вопросы 1. Поясните, почему абсолютные деформации менее информативны, чем относительные. 2. Чему равен коэффициент Пуассона для материала, не изменяющего свой объем при деформации? У какого материала µ меньше – у пробки или резины? 3. Что характеризует модуль Юнга Е? 4. Сформулируйте закон Гука. Рис.5.5 При растяжении/сжатии
Основная идея, которая положена в основу расчетов конструктивных элементов машин, заключается в том, что напряжения в них не должны превышать некоторых предельных значений, которые являются «опасными» для них. С этой точки зрения конструкция должна работать в наиболее благоприятных условиях, что и обеспечивает её долговечность и надежность работы. Возникает вопрос – что такое «опасное» напряжение? Ответом может служить следующее положение – «опасным» считается такое напряжение, превышение которого может привести (но не обязательно приводит) к разрушению или нежелательному поведению конструкции. Очевидно, что для пластичных материалов опасным напряжением является предел текучести σт. Превышение действующими в конструкции напряжениями предела текучести может привести к необратимым деформациям (хотя и не к разрушению) и конструкция не сможет существовать в заданных размерах. Для хрупких материалов предел текучести не является опасным напряжением, т.к. не сопровождается сколько-нибудь значительными изменениями размеров. В то же время превышение предела прочности (временного сопротивления) может привести к разрушению. Следовательно, в этом случае опасным напряжением является предел прочности σв. Почему выше употребляется словосочетание «может привести»? Здесь мы близко подходим к вероятностному характеру явлений в природе. Действительно, большинство явлений в природе носит недетерминированный характер. Например, применительно к механическим свойствам материалов можно сказать, что, если мы измерим значение предела текучести какого либо материала на конкретном образце, то не обязательно получим то значение, которое указано в справочнике для этого материала и даже не то значение, которое было получено в предыдущем опыте на этом же материале. Иными словами, значения любых механических свойств имеют некоторый разброс, который зависит от многих причин. Наша задача учесть это явление и не допустить появление в конструкции напряжений, превышающих даже самое низкое из «разбросанных» значений рассматриваемой характеристики механических свойств. Для этого необходимо гарантированно «отгородиться» от нежелательных значений напряжений. Поэтому вводится некоторый коэффициент запаса, обеспечивающий требуемый барьер. Его обозначают для пластичных материалов – nпл., а для хрупких материалов – nхр.. Тогда максимально действующие напряжения в конструкциях можно назвать допускаемыми (их принято обозначать в квадратных скобках) и определять по следующим соотношениям: [σ]пл.= σт/nпл. [σ]хр.= σв/nхр.
По своей сути коэффициенты запаса должны удовлетворять следующему неравенству nпл.,nхр.≥1. Конкретные значения коэффициентов запаса выбираются исходя из условий работы и ответственности той или иной конструкции, ее стоимости и затрат по замене в случае выхода из строя. Чем деталь более ответственна, тем коэффициент запаса для нее выше. Данные по их значениям приведены в справочных пособиях, а также берутся из опыта работы подобных конструкций. Завышенное значение коэффициента запаса по напряжениям - это всегда ненужный расход материала, дополнительные затраты на изготовление детали и ее эксплуатацию. С учетом вышесказанного получаем следующее условие прочности по напряжениям – действующие нормальные напряжения в конструкции не должны превышать допускаемых напряжений, т.е.
σ≤[σ]пл.,[σ]хр.
где σ - действующие в конструкции нормальные напряжения.
При растяжении/сжатии. Из вышесказанного следует, что условие прочности при растяжении/сжатии выглядит следующим образом: σ ≤ [σ где: σ – действующие напряжения в конструкции; [ σ ] – допускаемые напряжения в конструкции. При условии, что σ=N/А, из формулы (1) вытекает основное соотношение для условия прочности при растяжении/сжатии: N/А ≤ [ σ ] С помощью этой формулы можно выполнить четыре различных вида расчетов на прочность при растяжении/сжатии: Проверочный расчет. Задано: внешние нагрузки (т.е. тем самым определена внутренняя сила N), площадь поперечного сечения А, допускаемое напряжение [ σ ]. Требуется: проверить выполнимость формулы (2). Решение: Если формула (2) выполняется, то говорят, что прочность обеспечена. Если формула (2) не выполняется, то необходимо уменьшать внешнюю нагрузку (следовательно и внутреннюю силу N) или увеличить площадь поперечного сечения А.а также переходить к более прочным материалам с большими значениями [σ]. Проектный расчет. Задано: внешние нагрузки (т.е. внутренняя сила N) и допускаемое напряжение [ σ ]. Требуется: рассчитать минимально возможную площадь поперечного сечения А. Решение: Из формулы (2) следует, что минимально возможная площадь поперечного сечения может быть определена как: А≥N/[σ].
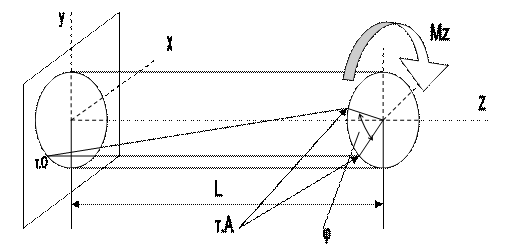
I. Определение. Примеры. Кручением называется такой вид нагружения бруса, при котором в каждом поперечном сечении возникает только один внутренний силовой фактор – момент, действующий вокруг продольной оси бруса. Так как мы приняли, что продольная ось бруса – это ось z, то этот момент можно обозначить – Mz. Так - как по сути такое нагружение вызывает скручивание вокруг оси z (рис.7.1), то и момент чаще всего называют «крутящим моментом» и обозначают - Мк .
Рис.7.1.
Как правило, кручению подвергаются брусья круглого поперечного сечения. Если внешний момент обозначить через Мz, то внутренний момент обозначим как Мк. Он определяется как и ранее по методу сечений и равен алгебраической сумме всех внешних нагрузок (заданных моментов) в рассматриваемой после рассечения части бруса. Выделим в брусе три разных поперечных сечения: первое в заделке, а второе и третье на некотором расстоянии от первого по длине бруса (рис.7.7). Опыт показывает, если на конце бруса приложить момент вокруг оси z, то: 1) сечение I остается на месте (неподвижно); 2) сечение II повернется на некоторый угол вокруг оси z относительно сечения I, а сечение III повернется на некоторый угол вокруг оси z относительно сечения II; 3) расстояние, между сечениями до и после нагружения и полная длина бруса в процессе нагружения не изменяются; 4)если расстояние между сечениями I, II и III одинаковое, то угол, на который сечение II повернется относительно сечения I и угол, на который сечение III повернется относительно сечения II, будут равны между собой.
Деформации при кручении. Рассмотрим деформации при кручении. Выделим прямую линию ОА, параллельную продольной оси бруса. Пусть на свободном конце бруса приложен крутящий момент вокруг оси z – Мz. Так как левая точка прямой ОА находится в заделке, то она остается неподвижной, а правая точка А переместится в некоторое новое положение по торцевому поперечному сечению. При этом угол, который образуется новым и старым положением т.А при соединении этих точек с центром сечения (угол φ) называется абсолютным углом закручивания.
Рис.7.4
Абсолютный угол закручивания измеряется в радианах. Введем в рассмотрение и относительный угол закручивания θ из соотношения θ = φ/L. Этот угол измеряется в радианах, отнесенных к единице длины. Рассмотрим искажение первоначально прямоугольного элемента боковой поверхности вала при кручении (рис.7.5).
Рис.7.5
Первоначально прямоугольный элемент искажается в параллелограмм. Такое искажение называется «чистым сдвигом», а угол γ – носит название «угол сдвига».
Напряжения при кручении. Рассмотренный выше характер деформированного состояния является следствием действия напряжений, называемых касательными, так как они направлены по касательной к боковой поверхности бруса. Их обычно обозначают τ, и они показаны на следующем рис.7.6.
Рис.7.6
Как отмечалось ранее, расстояния между поперечными сечениями не изменяются, следовательно, можно сделать вывод об отсутствии нормальных напряжений вдоль продольной оси Z. Учитывая, что касательные напряжения подчиняются «закону парности» (касательные напряжения на взаимно-перпендикулярных гранях равны по величине и направлены в противоположные стороны), окончательно получим, что напряженное состояние при «чистом сдвиге» будет выглядеть следующим образом (рис.7.7):
Рис.7.7
Можно показать, что распределение касательных напряжений по поперечному сечению носит линейный характер (рис.7.8) и они определяются по формуле
τ = (Mk ρ)/Iρ где: Mk – внутренний крутящий момент в рассматриваемом поперечном сечении; ρ – расстояние от центра поперечного сечения до произвольной его точки; Iρ – полярный момент инерции поперечного сечения.
Рис.7.8
Из этого соотношения можно сделать следующие выводы: 1. касательные напряжения в поперечном сечении изменяются по линейному закону в зависимости от расстояния от центра ρ. 2. в центре тяжести поперечного сечения при ρ=0 касательные напряжения равны 0 3. на боковой поверхности (наиболее удаленные точки поперечного сечения, ρ=D/2) касательные напряжения достигают максимального значения. Максимальное значение касательных напряжений равно
τmax=(Mk D/2)/Iρ=Mk/Wρ, где Wρ – полярный момент сопротивления сечения (для круглого поперечного сечения Wρ = 0,2 D3).
Кручении. По аналогии с растяжением/сжатием условие прочности выглядит следующим образом: τmax ≤ [τ],
где [τ] – допускаемое касательное напряжение. Допускаемое напряжение для пластичных и хрупких материалов определяется как и ранее по соотношениям:
[τ]пл. = τт/nпл. [τ]хр. = τв/nхр . Здесь обозначено: τт,τв – предел текучести для пластичных материалов и предел прочности для хрупких материалов при сдвиге соответственно; nпл., nхр. – коэффициенты запаса прочности для пластичных и хрупких материалов при сдвиге соответственно. Отметим, что здесь предполагается, что механические свойства материалов определяются в опытах на кручение. Заменяя в условии прочности полученное ранее выражение для τmax получим окончательное соотношение для условия прочности при кручении: Mk/Wρ ≤ [τ] или для брусьев с круглым поперечным сечением Mk/0,2D3 ≤ [τ] Отметим, что данное условие прочности должно применяться для поперечного сечения с наибольшим внутренним крутящим моментом. Такое сечение называется опасным. Из приведенных формул вытекает четыре различных вида расчетов на прочность при кручении: Проверочный расчет. Задано: внешние нагрузки (т.е. тем самым определен внутренний крутящий момент вдоль оси бруса Mk), диаметр поперечного сечения D, допускаемое напряжение [ τ ]. Требуется: проверить выполнимость условия прочности. Решение: Если условие прочности выполняется, то говорят, что прочность обеспечена. В противном случае необходимо уменьшать внешнюю. нагрузку, (следовательно и внутренний крутящий момент), увеличивать площадь поперечного сечения D или переходить к более прочным материалам с большими значениями [τ]. Проектный расчет. Задано: внешние нагрузки (внутренний крутящий момент Mk) и допускаемое напряжение [ τ ]. Требуется: рассчитать минимально возможный диаметр поперечного сечения D. Решение: Из условия прочности следует, что минимально возможный диаметр поперечного сечения может быть определен по формуле: D ≥ 3√Mk/0,2[τ]. Лекция 8. Прямой изгиб 8.1. Основные определения Изгибом называется такой вид нагружения, при котором ось бруса (и, собственно брус) под действием внешних нагрузок только искривляется, оставаясь в одной плоскости. Рассмотрим закрепленный в опорах брус, у которого продольная ось совпадает с координатной осью Z. При этом необходимо ответить на следующие вопросы: -какие внешние нагрузки могут привести к такой деформации бруса? -какие внутренние силовые факторы при этих внешних нагрузках будут действовать в поперечных сечениях? Ответ на первый вопрос представлен на рис.8.1(слева), а на второй - справа (при этом использован метод сечений).
Рис.8.1
Первая схема (действие сосредоточенной силы P, параллельной оси Y) приводит к возникновению в поперечных сечениях двух внутренних силовых факторов- внутренней силы Qy (она называется «поперечной» или «перерезывающей») и внутреннего изгибающего момента Mx (индекс «x» указывает на то, что изгиб происходит вокруг оси X). Эти внутренние силовые факторы определяются по следующим зависимостям
Qy = P, Mx = P L Вторая схема (действие распределенной нагрузки q, параллельной оси Y, приводит к возникновению в поперечных сечениях тех же двух внутренних силовых факторов внутренней силы Qy и внутреннего изгибающего момента Mx) В этом случае они определяются по соотношениям:
Qy = qL, Mx = qL L/2 = qL2/2 Третья схема (действие сосредоточенного момента M в плоскости YZ приводит к возникновению в поперечных сечениях только одного внутреннего силового фактора – изгибающего момента Mx) который определяется по соотношению:
Mx = M Изгиб, при котором брус деформируется в плоскостях YZ или XZ, называется прямым изгибом. Если изгиб происходит в плоскостях, наклоненных к указанным плоскостям YZ и XZ под некоторым углом, то такой изгиб называется косым. Если в поперечных сечениях бруса возникают поперечная (перерезывающая) сила и изгибающий момент,., то такой изгиб называют «поперечным», а если только один изгибающий момент-., «чистым» изгибом. 8.2. Правило знаков Qy, Mx Одним из основных моментов при рассмотрении деформации изгиба является построение эпюр внутренних силовых факторов – поперечной силы и изгибающего момента. Для правильного построения указанных эпюр ведем следующее правило знаков внутренних силовых факторов:
для Qy - будем считать поперечную силу положительной, если она вращает рассматриваемую часть бруса (при использовании метода сечений) по часовой стрелке и отрицательной, если она вращает рассматриваемую часть бруса против часовой стрелки; для Mx - будем считать момент положительным, если он изгибает рассматриваемую часть бруса (при использовании метода сечений) выпуклостью вниз и отрицательным, если он изгибает рассматриваемую часть бруса выпуклостью вверх. Указанные правила знаков на практике сводятся к следующему: а) для составления уравнение поперечной силы на каком-либо участке, необходимо в правой части равенства записать внешние сосредоточенные силы (заданные и эквивалентные от заданных распределенных нагрузок),приложенные к рассматриваемой после рассечения части бруса в соответствии с правилом знаков для поперечных сил Qy; б) для составления уравнения изгибающего момента на каком-либо участке необходимо в правой части равенства записать сумму моментов внешних нагрузок, действующих на рассматриваемую после рассечения часть бруса, в соответствии с правилом знаков для изгибающих моментов Mx.
8.3. Дифференциальные зависимости между Qy, Mx и q при изгибе Можно показать, что при прямом изгибе, например в плоскости YZ между Qy (z), Mx (z) и q (z) справедливы следующие дифференциальные соотношения (формулы Журавского): dMx(z)/dz = Qy(z) dQy(z)/dz = q(z)
При построении эпюр внутренних силовых факторов при изгибе пользуются << Правилами >>, вытекающими из этих соотношений: · если q(z) ≡ 0
|
||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.012 с.) |







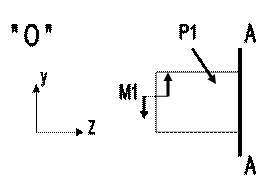

 ример I. Какая сила действует в поперечном сечении бруса (рис.4.1)?
ример I. Какая сила действует в поперечном сечении бруса (рис.4.1)? Р» - Рассекаем брус в интересующем нас сечении (рис.4.2)
Р» - Рассекаем брус в интересующем нас сечении (рис.4.2)







 «О» - Отбрасываем одну из частей бруса
«О» - Отбрасываем одну из частей бруса «З»- Для сохранения равновесия заменяем действие отброшенной части на оставшуюся часть бруса неизвестной пока внутренней силой
«З»- Для сохранения равновесия заменяем действие отброшенной части на оставшуюся часть бруса неизвестной пока внутренней силой 

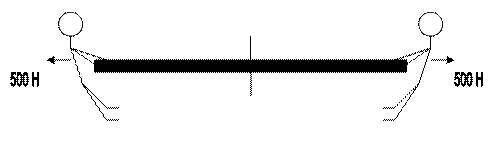

 «У» -уравновешиваем неизвестную внутреннюю силу и внешнюю нагрузку. В итоге получим:
«У» -уравновешиваем неизвестную внутреннюю силу и внешнюю нагрузку. В итоге получим: