
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эпюры гидростатического давленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Эпюры гидростатического давления - графическое изображение распределения ГСД на плоские фигуры.
Рисунок 16 - Эпюра гидростатического давления.
Давление на контур АВСДЕ справа будет равно атмосферному. Слева на контур АВ действует атмосферное давление, а на контур ВСДЕ действует заполняющая резервуар жидкость и атмосферное давление, которое уравновешивается Тогда эпюру ГСД можно представить в следующем, рассчитав избыточные давления в точках В, С, Д, Е.
Представив избыточные давления в каждой точке векторами в определенном масштабе, с учетом второго свойства ГСД строим эпюру, откладывая значения давлений в точках по нормали к стенке. Эпюра ГСД на стенку ВС представляет собой треугольник, т.к. изменение давления по глубине линейно. Эпюра давления на стенку СД будет представлять собой трапецию, т.к. в точке С давление Рассмотрим более сложный случай, когда плоская стенка подвержена давлению жидкости с двух сторон. С левой стороны глубина равна
Рис.17. Эпюры гидростатического давления Суммарная эпюра получится графическим вычитанием эпюр. На рисунке 17 она представлена в виде трапеции АМNС.
Сила давления на плоскую стенку. Положение Центра давления
Определим как рассчитывается сила гидростатического давления на плоскую стенку, которая наклонена под углом
Рисунок 18 - К определению силы давления на плоскую стенку.
На каждый бесконечно малый элемент площади
Тогда элементарная сила Суммарная сила давления на всю площадь со может быть получена интегрированием по площади
где Известно, что статический момент площади равен произведению координаты центра тяжести на площадь фигуры:
откуда можно записать, что суммарная сила гидростатического давления равна:
где Таким образом, сила гидростатического давления на плоскую поверхность равна произведению гидростатического давления в центре тяжести этой поверхности на ее площадь. Центром давления называется точка приложения полной силы гидростатического давления, действующей на данную поверхность. Для определения положения центра давления воспользуемся известной теоремой статики: момент равнодействующей силы равен сумме моментов сил ее составляющих. Т.е. Из этого выражения можно найти искомую координату центра давления (точки D):
где Но момент инерции относительно любой оси может быть выражен через моментинерции относительно центральной оси
где а - расстояние между осями (в нашем случае Тогда Используя уравнение связи между глубиной h и координатой y, получим уравнение для определения глубины погружения центра давления:
Это выражение показывает, что центр давления лежит всегда ниже центра тяжести (кроме давления на горизонтальную плоскость, когда они совпадают).
|
|||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 416; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.40.81 (0.008 с.) |

 Рассмотрим распределение нормальных напряжений (ГСД) на плоскую стенку резервуара с жидкостью (рис. 16). Пусть на поверхности жидкости действует атмосферное давление.
Рассмотрим распределение нормальных напряжений (ГСД) на плоскую стенку резервуара с жидкостью (рис. 16). Пусть на поверхности жидкости действует атмосферное давление. справа.
справа. ;
;  ;
;  .
. . Эпюра давления на дно ЕД будет прямоугольником, т.к.
. Эпюра давления на дно ЕД будет прямоугольником, т.к. 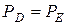 .
. , а с правой -
, а с правой -  (рис. 17). В этом случае эпюры будут представлять собой два треугольника: слева - высотой
(рис. 17). В этом случае эпюры будут представлять собой два треугольника: слева - высотой 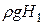 , справа высотой
, справа высотой 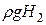 .
.
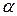 , при одностороннем воздействии жидкости (рис. 18). Одну координатную ось направим вдоль стенки, а другую по линии пересечения стенки со свободной поверхностью. Для удобства развернем проекцию стенки в плоскость чертежа. Выделим на ней фигуру площадью
, при одностороннем воздействии жидкости (рис. 18). Одну координатную ось направим вдоль стенки, а другую по линии пересечения стенки со свободной поверхностью. Для удобства развернем проекцию стенки в плоскость чертежа. Выделим на ней фигуру площадью  . Между любой координатой у и глубиной погружения h существует следующая связь:
. Между любой координатой у и глубиной погружения h существует следующая связь:  .
.
 действует элементарная сила
действует элементарная сила  , но давление в центре тяжести
, но давление в центре тяжести  .
. .
. ,
, - статический момент площади относительно оси ОХ.
- статический момент площади относительно оси ОХ. ,
, или
или 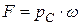 ,
, - давление в центре тяжести.
- давление в центре тяжести. .
. ,
, - момент инерции площади относительно оси ОХ.
- момент инерции площади относительно оси ОХ. (оси, проходящей через центр тяжести фигуры).
(оси, проходящей через центр тяжести фигуры). ,
, )
) или
или 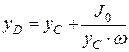 .
. .
.


