
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация отверстий и насадковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Истечение жидкости через отверстия, насадки, короткие трубы и из-под затворов часто встречаются в практике. К этому виду относятся истечения из отверстий резервуаров, через водоспуски. Отверстием в тонкой стенке называется такое отверстие, когда величина толщину стенки не влияет на форму струи и условия истечения жидкости (δ <0,2d, где: δ - толщина стенки, d - диаметр отверстия). Отверстие называется малым, если диаметр или другой линейный размер (например, сторона прямоугольника, для прямоугольного отверстия) будет меньше 0,1Н (где: Н-напор над центром тяжести отверстия). Насадком называется короткий патрубок герметически присоединенный к отверстию в тонкой стенке, длина которого в несколько раз больше внутреннего диаметра (обычно L = 3÷5d).Насадки делятся на три основных типа: цилиндрические, конические я коноидальные, цилиндрические насадки могут быть внешними или внутренними, конические и коноидальные могут быть сходящимися и расходящимися (см. рис. 60).
Рисунок 60 - Типы отверстий и насадков: а)отверстие в тонкой стенке; б)цилиндрические насадки; в)конические насадки; г)коноидальные насадки При истечении через отверстие происходит сжатие струи при выходе из резервуара, т.к. струйки меняют направление движения на 90° и движение происходит по непараллельным траекториям. Сжатое сечение образуется на некотором расстоянии от отверстия. Сжатие может быть совершенным, если границы отверстия достаточно удалены от стенок (находятся на расстоянии не менее 3-х линейных размеров) и стенки не оказывают влияния на сжатие струи. Но сжатие может быть и несовершенным, если одна или несколько сторон отверстия расположены достаточно близко к стенкам. Полным, сжатием называется сжатие при истечении из отверстия расположенного на некотором отдалении от стенок, а если отверстие касается хотя бы одной стороной стенки, то сжатие будет неполным (со стороны прилегающей стенки сжатия происходить не будет) (см. рис. 61).
Рисунок 61 - Сжатие струи: а) совершенное, б) несовершенное, в) полное, г)неполное.
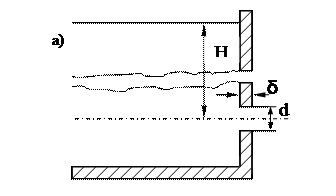
Истечение через малые отверстия в тонкой стенке Истечение в атмосферу Предположим, что есть резервуар в боковой стенке которого выполнено малое отверстие (рис. 61). Уровень жидкости в резервуаре будем считать постоянным. Проведем плоскость сравнения через центр тяжести сжатого сечения и выберем два расчетных сечения: 1-1 по свободной поверхности жидкости и С-С в сжатом сечении.
Рисунок 61 - Схема истечения из отверстия.
Составим уравнение Бернулли для этих двух сечений.
где: Н - напор над центром тяжести отверстия, Ра - атмосферное давление, V - скорость на свободной поверхности жидкости, Vc - в сжатом сечении струи, α- коэффициент Кориолиса, ξ- коэффициент местного сопротивления.
Обозначим через Но полный напор в сечении 1-1, тогда уравнение примет вид:
Отсюда найдем выражение для средней скорости в сжатом сечении:
так как Н ≈ Но, а V1≈0. A φ= Коэффициент скорости представляет собой отношение действительной скорости истечения Vc к скорости истечения идеальной жидкости
При истечении через отверстия или короткие насадки можно считать, что потеря напора состоит только из местных потерь, а потери на трение отсутствуют. Определим расход жидкости через отверстие из уравнения неразрывности: Q = Vcхωс = ωεφ где ωс- площадь сжатого сечения струи, ω - площадь сечения отверстия, ε - коэффициент сжатия струи равный ωс/ω. Коэффициент сжатия характеризует степень сжатия струи. Обозначим коэффициент расхода μ=εφ, тогда окончательную формулу расхода жидкости через отверстие можно представить в виде: Q=μω Коэффициент расхода характеризует отношение действительного расхода Q к расходу идеальной жидкости Qид=ω μ=Q/ω Для малых отверстий в тонкой стенке с совершенным сжатием коэффициент расхода μ≈0,6-0,62. Однако, необходимо отметить, что коэффициенты расхода, сжатия и скорости зависят от режима истечения (числа Рейнольдса), результаты исследований А.Д. Альтшуля представлены на рисунке 62.
Рисунок 62 - Зависимость μ, φ, ε от Re
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.106.211 (0.01 с.) |




 ,
, , где
, где 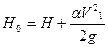 .
. или Vc=φ
или Vc=φ 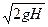 ,
,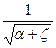 - коэффициент скорости.
- коэффициент скорости. :
: .
.



