
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Истечение через затопленное отверстиеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При истечении из отверстия в тонкой стенке под уровень, в области выхода образуется сжатое сечение С-С, в котором распределение давления подчиняется гидростатическому закону. Напишем уравнение Бернулли, предполагая установившееся движение.
Пренебрегая членом αV21/2g ввиду его малости и, определяя давление Рc как Рc = Рa + pgH2, получим: H1=H2+(α+ξ)V2c/2g или (α+ξ)V2c/2g= H1-H2. Следовательно, скорость в сжатом сечении С-С будет равна: Vc= Формула расхода при истечении через затопленное отверстие будет иметь вид: Q = Vc хω = ωεφ Формула аналогична формуле для незатопленного отверстия. Установлено, что коэффициент расхода также мало отличается (на 2-3%) от коэффициента расхода при истечении через незатопленное отверстие.
Истечение через насадки
При значительной толщине стенки характер явлений, наблюдаемых при истечении, существенно меняется из-за влияния, оказываемого на струю толстой стенкой. Насадком называется короткий патрубок герметически присоединенный к отверстию в тонкой стенке, длина которого в несколько раз больше внутреннего диаметра (обычно L=3÷5d). Струя жидкости после выхода из сосуда подвергается некоторому сжатию, но затем постепенно расширяется и заполняет все поперечное сечение насадка. Т.е. сжатие происходит только внутри насадка, поэтому при расчете истечения через насадки необходимо учитывать, что коэффициент сжатия ε=1, а, следовательно, коэффициент расхода равен коэффициенту скорости μ=φ.
Рисунок 63 - Истечение через насадок.
Определим расход через цилиндрический насадок (рис 63). Запишем уравнение Бернулли для сечений 1-1 и С-С относительно плоскости сравнения 0-0, проходящей через центр тяжести поперечного сечения насадка:
где Hо=Н+αV2/2g,
hвак - вакуумметрическая высота в сжатом сечении внутри насадка.
Тогда скорость в сжатом сечении можно определить по формуле:
Расход жидкости, проходящий через насадок можно рассчитать: Q = Vcхωс=ωεφ но hвак = 0,75 Н0, и тогда, подставив это значение в предыдущую формулу, получим: Q = ωμ Сопоставляя полученную зависимость с формулой для расхода через малое отверстие в тонкой стенке, отметим, что пропускная способность насадка по сравнению с малым отверстием увеличивается на 33%. Это объясняется наличием вакуума в сжатом сечении внутри насадка, что заставляет жидкость «всасываться» в насадок.
Из равенства hвак = 0,75 Н0 видно, что в конечном счете вакуум зависит от напора над центром тяжести поперечного сечения насадка. В частном случае при истечении воды предельное значение вакуума hвак = 10,33 м вод. ст., что соответствует наибольшему возможному напору воды Н0 ≈ 13,7 м. При больших напорах в насадке возможен разрыв струи и насадок перестанет работать полным сечением, струя не будет касаться стенок насадка, вакуум в нем не образуется, что приведет к снижению расхода.
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.99.6 (0.007 с.) |

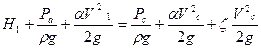 .
. .
. = ωμ
= ωμ 
 .
. ,
,
 .
. = ωμ
= ωμ  ,
, .
.


