
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силы, действующие в жидкости. ГидростатическоеСодержание книги
Поиск на нашем сайте
Гидростатика
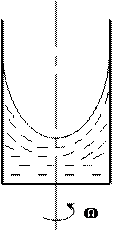
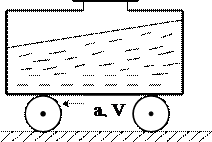
Силы, действующие в жидкости. Гидростатическое Давление и его свойства Гидростатикой называется раздел гидравлики, рассматривающий равновесие жидкостей и их взаимодействие с твердыми стенками. Жидкость, находящаяся в покое, характеризуется свойствами, очень близкими к свойствам идеальной жидкости, т.к. в ней не проявляются силы вязкости. Она может находиться в абсолютном или относительном покое, при этом на нее действуют массовые и поверхностные силы. Массовые силы пропорциональны массе жидкого тела или ее объему (для однородных жидкостей), к ним относятся силы тяжести, инерции. Поверхностные силы распределены по поверхности и пропорциональны величине этой поверхности - силы давления. Абсолютный покой жидкости - это ее покой относительно земли. Например, сосуд, наполненный жидкостью, стоит на столе и на жидкость действует только сила тяжести (см. рис 6а). Относительный покой - это равновесие жидкости в движущемся сосуде, когда помимо силы тяжести действует еще одна сила - сила инерции, постоянная во времени. Например, сосуд с жидкостью вращается вокруг своей вертикальной оси, при этом на каждую частицу жидкости действует сила тяжести и центробежная сила. Другим примером является ускоренное или замедленное движение цистерны, заполненной жидкостью. На жидкость действуют две силы: сила тяжести и сила инерции. И в одном и в другом случае жидкость находится в покое относительно стенок сосуда (см. рис. 6б).
а) абсолютный б) относительный Рисунок 6 – Примеры абсолютного и относительного покоя жидкости. Установим основные положения, связанные с понятием гидростатического давления. Возьмем некоторый объем (см. рис. 7), рассечем его пополам и мысленно отбросим объем I, заменив, для сохранения равновесия, его воздействие на объем II силой
Рисунок 7 - Давление в жидкости.
Однако,
будет являться гидростатическим давлением в данной точке. Но на практике чаще оперируют понятием среднего гидростатического давления. Единицей измерения давления в системе СИ является 1Па= 1Н/м2. Рассмотрим свойства гидростатического давления. 1. Гидростатическое давление направлено всегда по внутренней нормали к площадке, на которую это давление действует. Если касательное напряжение (см. рис.8) в точке (А)
Рисунок 8 – Первое свойство.
2. Гидростатическое давление действует одинаково по всем направлениям, т.е. не зависит от угла наклона площадки, на которую оно действует.
Рисунок 9 – Второе свойство. Массовой силой можно пренебречь, т.к. она на порядок меньше поверхностных. Силы давления можно выразить следующими зависимостями:
где Если тело находится в равновесии, то суммы проекций на оси всех действующих сил равны 0.
где:
После подстановки
3. Гидростатическое давление в точке зависит от ее координат в пространстве, т.е.
Рисунок 10 – Третье свойство.
1.2 Дифференциальные уравнения равновесия жидкости (уравнения Эйлера)
Рассмотрим равновесие жидкости (рис.11). Возьмем точку - объемные, пропорциональные массе параллелепипеда;
Рисунок 11 – К выводу уравнений Эйлера Рассмотрим сначала силы, действующие на жидкий параллелепипед по оси X. Проекция объемных сил
Следовательно, проекции объемных сил на все оси:
Гидростатическое давление в точке В обозначим
где Р - давление в точке А. Силы, действующие на грани равны:
Составим уравнение равновесия исследуемого нами жидкого объема относительно оси X:
Уравнение равновесия после подстановки и преобразования сможем записать в виде:
Окончательно уравнение равновесия относительно оси X будет иметь вид:
Аналогично получим уравнение равновесия относительно осей Y и Zи запишем полную систему уравнений, которые называются уравнениями Эйлера.
Впервые они были выведены в 1775 г. и выражают закон распределения гидростатического давления в дифференциальной форме. Для дальнейшего преобразования, умножим каждое из уравнений системы на
а, сложив их почленно, получим следующее выражение:
Левая часть представляет полный дифференциал давления
Функция Интегрируя функцию
где С - постоянная интегрирования. Для двух точек одного и того же объема данной однородной несжимаемой жидкости уравнение записывается в виде:
Дадим определение поверхности равного давления: это поверхность, проведенная в покоящейся жидкости таким образом, что давление во всех ее точках одинаково, т.е. -построенные для различных гидростатических давлений, они не имеют общих точек, т.е. не пересекаются; -всегда нормальны к направлению равнодействующей внешних объемных сил, приложенных к жидкости.
Центра давления
Определим как рассчитывается сила гидростатического давления на плоскую стенку, которая наклонена под углом
Рисунок 18 - К определению силы давления на плоскую стенку.
На каждый бесконечно малый элемент площади Тогда элементарная сила Суммарная сила давления на всю площадь со может быть получена интегрированием по площади
где Известно, что статический момент площади равен произведению координаты центра тяжести на площадь фигуры:
откуда можно записать, что суммарная сила гидростатического давления равна:
где Таким образом, сила гидростатического давления на плоскую поверхность равна произведению гидростатического давления в центре тяжести этой поверхности на ее площадь. Центром давления называется точка приложения полной силы гидростатического давления, действующей на данную поверхность. Для определения положения центра давления воспользуемся известной теоремой статики: момент равнодействующей силы равен сумме моментов сил ее составляющих. Т.е. Из этого выражения можно найти искомую координату центра давления (точки D):
где Но момент инерции относительно любой оси может быть выражен через моментинерции относительно центральной оси
где а - расстояние между осями (в нашем случае Тогда Используя уравнение связи между глубиной h и координатой y, получим уравнение для определения глубины погружения центра давления:
Это выражение показывает, что центр давления лежит всегда ниже центра тяжести (кроме давления на горизонтальную плоскость, когда они совпадают).
Гидродинамика
Режимы движения жидкости Одна из основных задач практической гидравлики - оценка потерь напора на преодоление гидравлических сопротивлений, возникающих при движении реальных жидкостей в различных гидравлических системах. Точный учет этих потерь во многом определяет надежность технических расчетов.
Рисунок 31 – Схема установки Рейнольдса
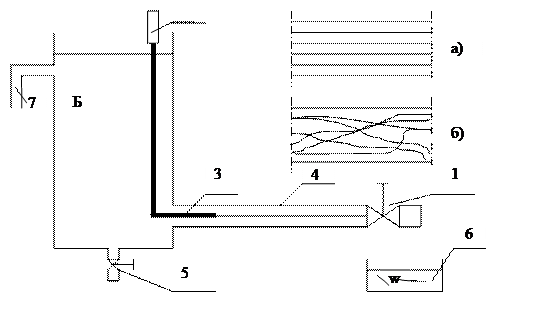
Рейнольдс пропускал жидкость из бака Б, в котором с помощью перелива 7 поддерживался постоянный уровень, через стеклянные трубки различного диаметра, регулируя скорость движения жидкости в них кранами 1 и 5. По тонкой трубке 3 с заостренным концом ко входу в стеклянную трубку 4 подводилась окрашенная жидкость из сосуда 2. Средняя скорость V в трубке 4, имеющей площадь сечения со определялась по объему жидкости W, поступившей в мерный сосуд 6 за время t (рис.31). Как показывают исследования, структура потока при различных скоростях течения различна. При малых скоростях течения в потоке жидкости появляются окрашенные струйки. Они движутся прямолинейно, без пульсаций, не перемешиваясь с соседними слоями жидкости (рис. 31а). Такое параллельно-струйное, спокойное движение жидкости без поперечного перемешивания и при отсутствии пульсации скорости и давления называют ламинарным (слоистым) режимом движения жидкости. При постепенном увеличении скорости движения жидкости при некоторой скорости течения параллельно-струйное движение нарушится, окрашенные струйки станут пульсирующими, появятся разрывы. А при дальнейшем увеличении скорости окрашенные струйки исчезнут, перемешавшись с потоком жидкости (рис. 316). Движение станет беспорядочным вследствие пульсации скоростей и давления, что и приводит к перемешиванию частиц жидкости. Движение жидкости, во время которого происходит пульсация скоростей и давления, называют турбулентным (беспорядочным) режимом движения. Обобщив результаты своих опытов, Рейнольде нашел общие условия, при которых возможны существование того или иного режима или переход одного режима к другому. Он установил, что основными факторами, определяющими характер режима, являются: средняя скорость движения жидкости V, внутренний диаметр трубы d, плотность жидкости р, динамическая вязкость rj. Для характеристики режима движения Рейнольде ввел безразмерный параметр Re, учитывающий влияние перечисленных факторов, называемый числом (или критерием) Рейнольдса.
Границы существования того или иного режима движения жидкости определяются двумя числами Рейнольдса, которые называются критическими: нижним ReKP.H.=2320 и верхним ReKp.B.=13800 (сам Рейнольдс получил несколько иные значения ReKP.H.=2000 Rckp.b.=12000). Значения скоростей, соответствующие этим значениям числа Рейнольдса, также называют критическими (нижней критической Vh.k. и верхней критической Vb.k.)- Таким образом, при Re < Rckp.h (соответственно, V< Vh.k) возможен только ламинарный режим, при Re> Reкр.н.B (V> Vв.к) - турбулентный, а при Тогда, для определения характера режима движения жидкости необходимо в каждом отдельном случае вычислять число Рейнольдса Re=Vd /v и сравнивать результат с критическими значениями. В настоящее время при расчетах принято исходить только из нижнего значения критического числа Рейнольдса Reкp.=2320 и считать режим ламинарным при Re < 2320, а турбулентным при Re> 2320. При этом движение в неустойчивой зоне исключается из рассмотрения, что приводит к некоторому запасу и большей надежности в гидравлических расчетах. С физической точки зрения критерий Re есть отношение сил инерции потока к силам трения при его движении. Определение режима движения жидкости в практических расчетах имеет очень важное значение. Опыты показали, что потери напора по длине потока при ламинарном режиме движения пропорциональны средней скорости в первой степени:
где: кл -коэффициент пропорциональности; V - средняя скорость течения потока Для турбулентного режима движения потери напора по длине потока пропорциональны средней скорости в степени n:
где: n – показатель степени, изменяющийся от 1,75 до 2. Покажем на графике (рис. 32) соотношение между потерями напора
Рисунок 32 - Зависимость
Сложение потерь напора. Во многих случаях при движении жидкостей в различных гидравлических системах (например, трубопроводах) имеют место одновременно потери напора на трение по длине и местные потери. Полная потеря напора в подобных случаях определяется как арифметическая сумма потерь всех видов. При определении потерь во всем потоке, допускается, что каждое сопротивление независимо от соседних. Поэтому общие потери складываются из суммы потерь, вызванных каждым сопротивлением. Если трубопровод состоит из нескольких участков длинами
где:
3.6 Влияние различных факторов на коэффициент
Наибольшую сложность при расчете потерь напора представляет собой расчет коэффициента Исследованиям влияния различных факторов на значение коэффициента гидравлического трения Результаты опытов Никурадзе представлены на графике В области ламинарного режима (Rе<2320) все опытные точки независимо от шероховатости стенок уложились на одну прямую(линия 1). Следовательно, При переходе от ламинарного режима к турбулентному коэффициент В области турбулентного режима можно выделить три зоны сопротивления. Первой является зона гладких труб, в которой Следующая зона называется зоной шероховатых труб (доквадратичной), на рисунке она представлена рядом кривых 3, стремящихся к некоторым определенным пределам. Коэффициент
Примерные границы областей следующие: зона гладких труб 4000 < Rе < 40 d/ зона шероховатых труб 40 d/ квадратичная зона Rе > 500 d/ Переход из одной зоны в другую можно истолковать следующим образом: до тех пор пока выступы шероховатостей полностью погружены в ламинарный пограничный слой (т.е Однако, трубы, применяемые на практике, имеют неоднородную и неравномерную шероховатость. Выяснением вопросов влияния на естественной шероховатости занимались многие ученые, наибольшую известность получили опыты Мурина Г.А. (для стальных труб). Подтвердив основные закономерности, установленные Никурадзе, эти опыты позволили сделать ряд важных, существенно новых выводов. Они показали, что для труб с естественной шероховатостью в переходной области
Рисунок 40 - Результаты опытов Мурина
3.7 Формулы для определения коэффициента Дарси
Для расчета коэффициента Дарси При ламинарном режиме (Rе < 2320) для определения в круглых трубах применяют формулу Пуазейля:
Формула выведена теоретически, что показано в разделе «Особенности течения при ламинарном режиме». В области перехода от ламинарного к турбулентному режиму λ рассчитывается по формуле Френкеля:
При турбулентном режиме существует три зоны: - для гидравлически гладких труб используется несколько формул; Наиболее часто используемые: Блазиуса
Конакова П.К. - для гидравлически шероховатых труб Альтшуля А.Д. где; кэ - эквивалентная равнозернистая шероховатость, аналогична Кольбрука – Уайта Границы использования этих формул могут определятся в диапазоне чисел Рейнольдса от 10 - в области квадратичного сопротивления (числа Рейнольдса более 500 Шифринсона Б.Л. Прандтля – Никурадзе Приведенные выше формулы наиболее полно и правильно учитывают влияние различных факторов на коэффициент гидравлического сопротивления трения. Они выбраны из большого числа формул, существующих в настоящее время. Формула Альтшуля А.Д. является наиболее универсальной и может применяться для любой из трех зон турбулентного режима. При небольших числах Рейнольдса она очень близка к формуле Блазиуса, а при больших числах Рейнольдса - преобразуется в формулу Шифринсона Б.Л.
Классификация трубопроводов
В современной технике применяются трубопроводы для перемещения разнообразных жидкостей, изготавливаемые из различных материалов. В зависимости от геометрической конфигурации и способов гидравлического расчета различают простые и сложные трубопроводы. Простым называют трубопровод, состоящий из одной линии труб, не имеющих боковых ответвлений. Он может выполняться из труб одного или различных диаметров, различных длин (рис. 41).
Рисунок 41 - Простые трубопроводы Сложным называют трубопровод, состоящий из основной магистрали и ряда отходящих от нее ответвлений (рис. 42). Сложные трубопроводы подразделяются на следующие виды: -параллельные, когда к основной магистрали параллельно подключена одна или несколько труб; -разветвленные или тупиковые, когда жидкость из магистрали подается в боковые ответвления, обратно в магистраль она не возвращается; -кольцевые, представляющие собой замкнутую сеть (кольцо), питаемую от магистрали.
В зависимости от величины местных потерь напора все трубопроводы можно разделить на гидравлически длинные и короткие. Трубопроводы, в которых основными потерями являются потери на трение Расход может быть сосредоточенным или непрерывным. Расход называется сосредоточенным, если точки отбора находятся на значительном расстоянии друг от друга, и непрерывным, если эти точки расположены очень близко одна от другой (рис. 43).
Рисунок 43 - Расход сосредоточенный и непрерывный
Рисунок 44 - Напорный и безнапорный трубопроводы.
Различают также трубопроводы напорные и безнапорные (рис. 44). В напорных жидкость находится под избыточным давлением и при полном заполнении всего поперечного сечения. Безнапорные трубопроводы работают неполным сечением и характеризуется наличием свободной поверхности.
Последовательное соединение При последовательном соединении трубопроводов различного диаметра исходят из того, что общие потери напора в трубопроводе равны сумме потерь напора на отдельных его участках. Допустим, что диаметры участков di различные, тогда общие потери напора равны сумме потерь на отдельных участках: H=h1+ h2+ ….+hп. Для гидравлически короткого трубопровода потери определяются по формулам Вейсбаха и Дарси-Вейсбаха, а для гидравлически длинного трубопровода потери определяются по
где К – модуль расхода. Или для всего трубопровода
Рисунок 52 - Схема последовательного соединения и построения характеристики
Часто используется графо-аналитические методы с построением гидравлических характеристик участков и сети, особенно при переменном расходе в сети. Характеристикой трубопровода или участка называется графическая зависимость потерь напора(давления) в трубопроводе от расхода жидкости.(h Для построения характеристики h=f(Q) необходимо рассчитать 5-7 точек кривой. При расчете последовательно соединенных трубопроводов необходимо помнить, что по всем участкам такого трубопровода протекает одинаковый расход. Кривая I соответствует гидравлической характеристике первого участка, кривая II -второго участка. Т.к общие потери во всем трубопроводе равны сумме потерь напора на двух участках, а расходы на участке 1 и участке 2 одинаковы, то для построения суммарной характеристики сложного трубопровода с последовательным соединением необходимо сложить гидравлические характеристики отдельных участков. При этом суммарную (общую) характеристику такой сети строят сложением ординат кривых I и II, представляющих собой характеристики h=f(Q) соответственно для 1-го и 2-го участков. Для этого проведем ряд прямых, параллельных оси ординат, каждая из которых пересечет обе кривые, и сложим ординаты точек пересечений этих прямых с кривыми. Получим ряд точек a,b,c, принадлежащих новой кривой I+II, которая представляет собой иск
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.216.109 (0.014 с.) |


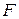 - силой гидростатического давления, которая действует по всей плоскости площадью
- силой гидростатического давления, которая действует по всей плоскости площадью 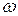 . Тогда среднее гидростатическое давление на площадку получим, разделив силу на площадь:
. Тогда среднее гидростатическое давление на площадку получим, разделив силу на площадь: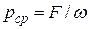 .
.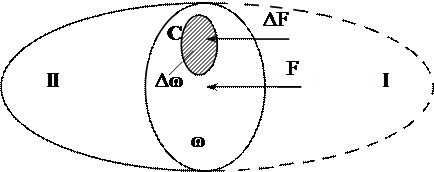
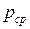 не выражает истинного гидростатического давления, т.к. в общем случае истинное давление в отдельных точках площадки может быть различным. Возьмем произвольную точку С и выделим около нее площадку, на которую будет действовать сила
не выражает истинного гидростатического давления, т.к. в общем случае истинное давление в отдельных точках площадки может быть различным. Возьмем произвольную точку С и выделим около нее площадку, на которую будет действовать сила 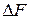 . Предел отношения
. Предел отношения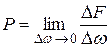
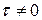 , то жидкость находится в движении и стремится занять положение, при котором
, то жидкость находится в движении и стремится занять положение, при котором 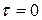 (точка В), т.к. растягивающие и касательные напряжения проявляются лишь при движении жидкости. По этой причине внешние силы, действующие на покоящуюся жидкость, могут быть только сжимающими.
(точка В), т.к. растягивающие и касательные напряжения проявляются лишь при движении жидкости. По этой причине внешние силы, действующие на покоящуюся жидкость, могут быть только сжимающими.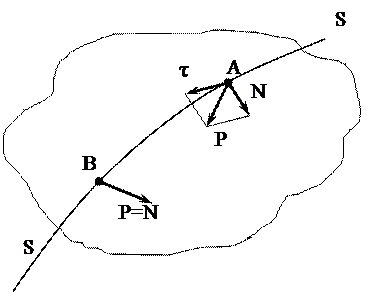
 Для доказательства выделим точку А и примем ее за начало прямоугольных координат (рис.9). Построим бесконечно малый тетраэдр со сторонами
Для доказательства выделим точку А и примем ее за начало прямоугольных координат (рис.9). Построим бесконечно малый тетраэдр со сторонами 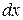 ,
, 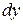 ,
, 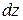 . Кроме сил давления на тетраэдр действует массовая сила, равная:
. Кроме сил давления на тетраэдр действует массовая сила, равная: 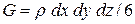
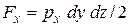
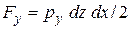
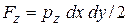
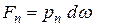
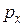 ,
, 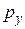 ,
, 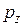 ,
, 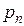 - средние гидростатические давления, действующие на соответствующие грани
- средние гидростатические давления, действующие на соответствующие грани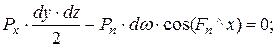
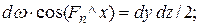
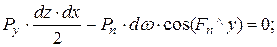
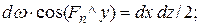
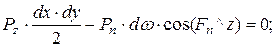
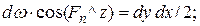
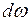 - площадь наклонной грани;
- площадь наклонной грани;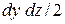 - проекция площади
- проекция площади 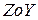 ;
;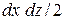 - проекция площади
- проекция площади 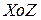 ;
;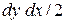 - проекция площади
- проекция площади 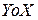 .
.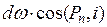 в исходные уравненная и преобразования, получим
в исходные уравненная и преобразования, получим 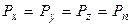 . Что и требовалось доказать.
. Что и требовалось доказать.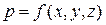 . Очевидно, что с увеличением глубины погружения точки давление в ней возрастает (рис. 10).
. Очевидно, что с увеличением глубины погружения точки давление в ней возрастает (рис. 10).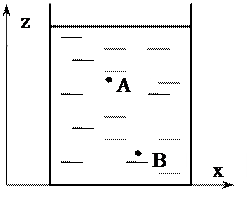
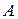 и выделим около нее параллелепипед со сторонами
и выделим около нее параллелепипед со сторонами 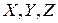 . Внешними силами здесь будут:
. Внешними силами здесь будут: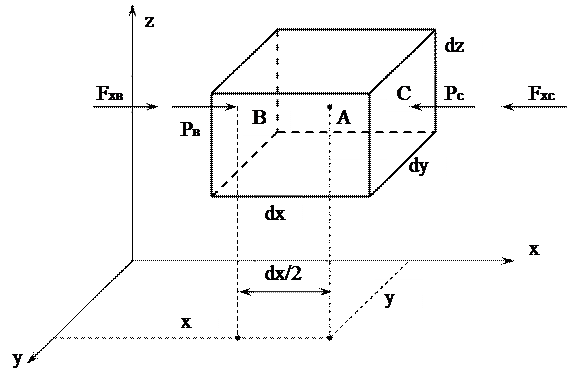 - силы гидростатического давления, действующие на грани параллелепипеда со стороны окружающей жидкости.
- силы гидростатического давления, действующие на грани параллелепипеда со стороны окружающей жидкости.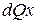 на ось X будет равна:
на ось X будет равна: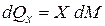 ;
;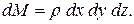
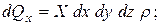
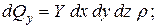
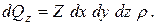
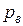 , а в точке С - через
, а в точке С - через 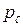 . Если давление изменяется по линейному закону и непрерывно, тогда:
. Если давление изменяется по линейному закону и непрерывно, тогда: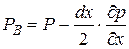 ;
; 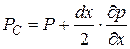
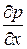 - градиент гидростатического давления;
- градиент гидростатического давления;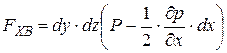 ;
;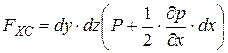
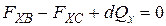
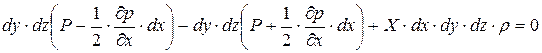
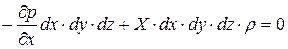
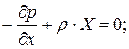
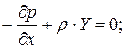
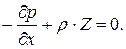
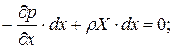
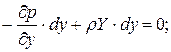
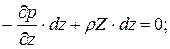
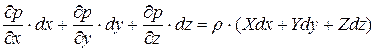 .
.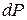 функции
функции 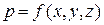 . А т.к. левая часть - полный дифференциал функции, то и правая тоже. Только в этом случае уравнение может иметь смысл. Для этого необходимо, чтобы существовала функция
. А т.к. левая часть - полный дифференциал функции, то и правая тоже. Только в этом случае уравнение может иметь смысл. Для этого необходимо, чтобы существовала функция 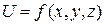 , производные которой были равны:
, производные которой были равны: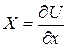 ;
; 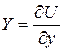 ;
; 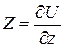 .
.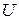 и обратная ей функция
и обратная ей функция 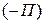 называются потенциальными. Следовательно, поле массовых сил потенциальное
называются потенциальными. Следовательно, поле массовых сил потенциальное 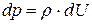 или
или 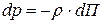 , где функция
, где функция 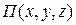 выражает потенциальную энергию поля массовых сил (сил тяжести и инерции).
выражает потенциальную энергию поля массовых сил (сил тяжести и инерции).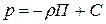 или
или 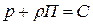 ,
,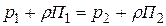 .
.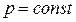 . Поверхности равного давления обладают следующими основными свойствами:
. Поверхности равного давления обладают следующими основными свойствами: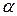 , при одностороннем воздействии жидкости (рис. 18). Одну координатную ось направим вдоль стенки, а другую по линии пересечения стенки со свободной поверхностью. Для удобства развернем проекцию стенки в плоскость чертежа. Выделим на ней фигуру площадью
, при одностороннем воздействии жидкости (рис. 18). Одну координатную ось направим вдоль стенки, а другую по линии пересечения стенки со свободной поверхностью. Для удобства развернем проекцию стенки в плоскость чертежа. Выделим на ней фигуру площадью  . Между любой координатой у и глубиной погружения h существует следующая связь:
. Между любой координатой у и глубиной погружения h существует следующая связь:  .
.
 действует элементарная сила
действует элементарная сила  , но давление в центре тяжести
, но давление в центре тяжести  .
. .
. ,
, - статический момент площади относительно оси ОХ.
- статический момент площади относительно оси ОХ. ,
, или
или 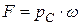 ,
, - давление в центре тяжести.
- давление в центре тяжести. .
. ,
, - момент инерции площади относительно оси ОХ.
- момент инерции площади относительно оси ОХ. (оси, проходящей через центр тяжести фигуры).
(оси, проходящей через центр тяжести фигуры). ,
, )
) или
или 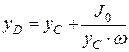 .
. .
.
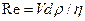 но
но 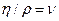 , тогда
, тогда 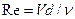 .
.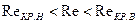 ,или
,или 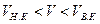 .) наблюдается неустойчивое состояние потока.
.) наблюдается неустойчивое состояние потока.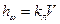 ,
,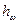 - потери напора по длине потока;
- потери напора по длине потока;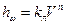

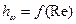
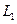

 различного диаметра
различного диаметра 

 с N местными сопротивлениями, то полную потерю напору находят по формуле:
с N местными сопротивлениями, то полную потерю напору находят по формуле:


 ,
,  ,…,
,…,  ,
,  ,
,  , …,
, …,  ,
,  ,
, 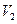 , …,
, …,  - коэффициенты сопротивлений и средние скорости для отдельных участков и местных сопротивлений.
- коэффициенты сопротивлений и средние скорости для отдельных участков и местных сопротивлений.
 , на который оказывают влияния многие параметры потока и трубопровода.
, на который оказывают влияния многие параметры потока и трубопровода. не проявляется, на рисунке точки располагаются вдоль наклонной кривой (кривая 2). Отклонение от этой кривой наступает тем раньше, чем больше шероховатость
не проявляется, на рисунке точки располагаются вдоль наклонной кривой (кривая 2). Отклонение от этой кривой наступает тем раньше, чем больше шероховатость  Рисунок 39 - Графики Никурадзе
Рисунок 39 - Графики Никурадзе ), они не создают различий в гидравлической шероховатости. Если же выступы шероховатостей выходят за пределы пограничного слоя (
), они не создают различий в гидравлической шероховатости. Если же выступы шероховатостей выходят за пределы пограничного слоя ( ), выступы шероховатости приходят в соприкосновение с турбулентным ядром и образуются вихри. Как известно, с увеличением Rе толщина слоя
), выступы шероховатости приходят в соприкосновение с турбулентным ядром и образуются вихри. Как известно, с увеличением Rе толщина слоя  ).
).

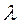
 .
. область применения (4000<Rе<105)
область применения (4000<Rе<105)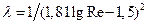 область применения (4000<Rе<Зх106)
область применения (4000<Rе<Зх106)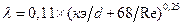 ,
, .
. d/кэ до 500
d/кэ до 500  .
. .
.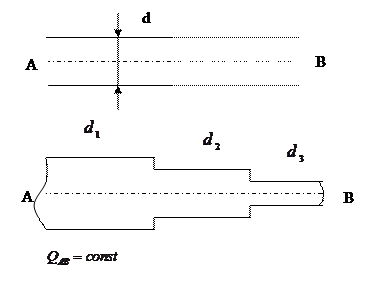
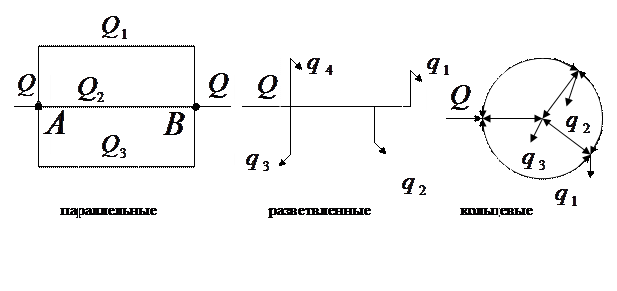 Рисунок 42 - Сложные трубопроводы
Рисунок 42 - Сложные трубопроводы , а местными потерями Им и скоростным напором
, а местными потерями Им и скоростным напором 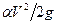 можно пренебречь называются гидравлически длинными. В этом случае местные потери напора
можно пренебречь называются гидравлически длинными. В этом случае местные потери напора  не должны превышать 5-10% от потерь на трение
не должны превышать 5-10% от потерь на трение 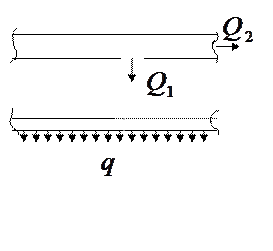
 формуле:
формуле: ,
,
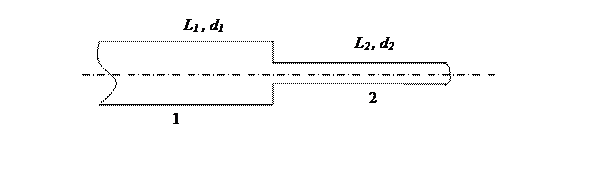
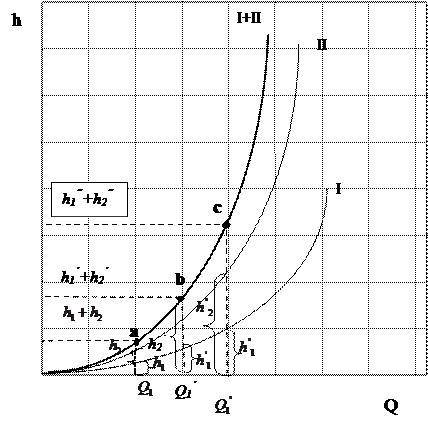
 .Изобразим эту зависимость графически (рис.52).
.Изобразим эту зависимость графически (рис.52).


