
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности течения при ламинарном режимеСодержание книги
Поиск на нашем сайте
Ламинарный режим характерен четким выделением отдельных струек. Рассмотрим распределение касательных напряжений, давления, скоростей при ламинарном режиме (рис. 33). Касательные напряжения. Касательное напряжение т на произвольном удалении г от центра трубы можно записать из основного уравнения равномерного движения.
где: I - гидравлический уклон, равный R- гидравлический радиус, равный В соответствии с уравнением Бернулли гидравлический уклон для всех струек одинаков. Следовательно, касательные напряжения будут изменяться линейно. Максимальное значение х у стенок трубы в прилипшем слое при Распределение давления. В этом случае действует закон статики, поэтому распределение давления происходит по гидростатическому закону. Наибольшее давление будет в точке С у нижней кромки трубы
Рисунок 33 - Распределение касательных напряжений, давлений и скоростей по живому сечению при ламинарном режиме.
Распределение скоростей. Касательные напряжения при ламинарном режиме можно выразить из закона вязкого трения Ньютона:
Приравняем два выражения
Из этого выражения, произведя преобразования и интегрирование, получим скорость:
Постоянную интегрирования C,определим из условий нулевой скорости на стенках трубы (U=0 при r=0),откуда
Окончательно закон распределения скоростей имеет вид
Эпюра скоростей в живом сечении представляет собой парабалоид вращения. Скорость изменяется от нуля в прилипшем слое у стенок трубы до Vmax на оси. Расход и средняя скорость. Элементарный расход в живом кольцевом сечении толщиной dr и удаленном от центра на расстояние г можно выразить по формуле:
Проинтегрировав это выражение от 0 до
Среднюю скорость определим из уравнения неразрывности
Сопоставив выражения для расчета максимальной скорости Vmax и средней скорости отметим, что они связаны соотношением:
Потери энергии (напора) и коэффициент Дарси.Формулу для определения потерь энергии на трение в круглой трубе можно получить, преобразовав формулу для расчета средней скорости, выразив в ней гидравлический уклон как
В общем случае потери энергии на трение выражается формулой Дарси-Вейсбаха:
С учетом известных соотношений:
Анализируя формулу, можно сделать вывод о линейной зависимости коэффициента Дарси
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

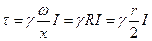 ,
,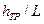
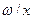
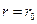 , а на оси при
, а на оси при 
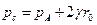 причем часто разницей давления по сечению трубы можно пренебречь и считать во всех точках его равным давлению в центре тяжести сечения на оси трубы.
причем часто разницей давления по сечению трубы можно пренебречь и считать во всех точках его равным давлению в центре тяжести сечения на оси трубы.




 ; при r=0;
; при r=0; 
 .
. , получим расход потока жидкости:
, получим расход потока жидкости: .
. , где
, где  , тогда:
, тогда: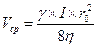 .
. , с учетом этого соотношения, закон распределения скоростей можно записать так:
, с учетом этого соотношения, закон распределения скоростей можно записать так: .
. , тогда
, тогда (формула Пуазеиля)
(формула Пуазеиля) .
. , получим значение коэффициента Дарси для ламинарного режима:
, получим значение коэффициента Дарси для ламинарного режима: .
. от числа Рейнольдса Re, а также о такой же зависимости потерь на трение (по длине)
от числа Рейнольдса Re, а также о такой же зависимости потерь на трение (по длине)  от средней скорости V.
от средней скорости V.


