Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бернулли для струйки и потока идеальной жидкостиСодержание книги
Поиск на нашем сайте
Воспользуемся основным законом механики, а именно: Равнодействующая всех сил, действующих на данное тело, равна массе тела, умноженной на ускорение, с которым движется это тело. Полная сила инерции равна: I = - m(dV/dt). Будучи отнесенной к единице массы, полная сила инерции даст единичную силу инерции. Ее проекции на координатные оси будут равны:
Теперь необходимо внести эти составляющие в уравнения Эйлера дл гидростатики и получим уравнения всех единичных сил, действующих движущейся жидкости. Преобразуем уравнения Эйлера к следующему виду:
Или после преобразований
Эти уравнения носят название дифференциальных уравнений Эйлера для движущейся идеальной жидкости. Они устанавливают связь между проекциями объемных, массовых сил и скоростей, давлением и плотностью жидкости и являются основой для изучения некоторых вопросов гидродинамики. Уравнения не учитывают ни си л тре н ия, ни сил сцепления (вязкости), т.к. уравнения получены из уравнений статики, а в статических уравнениях данные величины не фигурируют. Далее рассмотрим уравнения живых сил, для чего умножим уравнения у Эйлера на dx, dy, dz соответственно, и сложим их почленно:
Для установившегося движения в скобках слева стоит полный дифференциал давления dp. Справа будем иметь: dx/dt = Vx; dy/dt = VY; dz/dt = Vz Тогда VxdVx = d(Vx2/2); VydVy = d(VY2/2); VzdVz = d(Vz2/2). Но сумма полных дифференциалов трех составляющих скорости по осям х, у, z равна полному дифференциалу скорости: d(Vx2/2) +d(VY2/2) +d(Vz2/2) =d(V2/2) Окончательно получим закон живых сил в следующем виде: d(V2/2) = Xdx + Ydy +Zdz -dp/p Закон живых сил можно сформулировать в следующем виде: дифференциал кинетической энергии частицы идеальной жидкости при установившемся движении равен сумме элементарных работ сил тяжести и сил давления. Рассмотрим наиболее важный для практики случай движения жидкости: Расположим в несжимаемой жидкости, находящейся под действием силы тяжести в установившемся движении, оси координат так, что ось z была направлена вверх параллельно направлению действия силы тяжести. Тогда X=Y=0, Z=-g (знак «минус» поставлен, т.к. ось Z направлена вверх, а ускорение g вниз) и уравнение живых сил перепишется в следующем виде:
Перенеся все составляющие в левую часть, получим:
Разделим каждый член на g и сумму дифференциалов заменим дифференциалом суммы:
После интегрирования получим уравнение Бернулли для элементарной струйки жидкости в установившемся движении:
Дифференциал равен нулю, если под знаком дифференциала стоит постоянная величина. Все три члена уравнения Бернулли представляют собой механическую энергию, поэтому можно сделать следующее заключение: вдоль линии тока несжимаемой и невязкой жидкости запас механической энергии, отнесенный к единице массы, веса или объема остается постоянным. Механическую энергию жидкости, отнесенную к единице веса, называют полным напором; суммы энергии сил давления и положения, отнесенную к единице веса - статическим напором. Вдоль данной линии тока (в установившемся движении жидкости) сумма скоростного и статического напоров остается постоянной. Если вспомним, что P/pg пьезометрический напор, a z геометрический, а также введя понятие скоростного (динамического) напора V2/2g, то можно сказать, что сумма скоростного, пьезометрического и геометрического напоров вдоль линии тока есть величина постоянная. Так как сумма z+P/pg представляет собой удельную потенциальную энергию жидкости, a V2/2g- удельную кинетическую энергию, то уравнение Бернулли устанавливает постоянство полной энергии (суммы кинетической и потенциальной энергии) и является частным случае/закона сохранения энергии. Получим теперь уравнение Бернулли для потока идеальной жидкости, для чего подсчитаем полную энергию жидкости в живом сечении, умножив все составляющие на весовой расход элементарной струйки
Т.к. давление распределяется по закону гидростатики, то z+P/pg =const и может быть вынесено за знак интеграла. Кроме того, скорости всех элементарных трубок одинаковы, поэтому также выносится за знак интеграла. Тогда получим:
Возвратясь теперь к размерности удельной энергии, получим уравнение Бернулли для потока идеальной жидкости:
Уравнение не учитывает потерь напора и неравномерности распределения скоростей по сечению потока, возникающих при движении • реальной жидкости. Рассмотрим построение пьезометрической и напорной линии для случая движения идеальной жидкости (рис. 28). В случае идеальной жидкости полный напор (полная энергия) остается постоянной вдоль всего потока, а потенциальная и кинетическая энергии (гидростатический и скоростной напоры) могут переходить друг в друга. Например: уменьшение диаметра трубопровода приведет к увеличению скорости и скоростного напора, соответственно, давление в этом сечении (пьезометрический напор) уменьшится. Расположим в нескольких сечениях пьезометрические и гидродинамические трубки. Для идеальной жидкости во всех гидродинамических трубках уровень жидкости будет одинаков и выше, чем в пьезометрических, на величину скоростного напора (удельной кинетической энергии). Соединим уровни жидкости в пьезометрах - получим пьезометрическую линию. А, соединив уровни жидкости в гидродинамических трубках, получим напорную линию. Напорная линия представляет собой горизонтальную прямую.
Рисунок 28 - Пример построения пьезометрической и напорной линии для идеальной жидкости
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.116.33 (0.009 с.) |

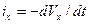 ,
, 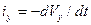 ,
, 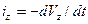 .
.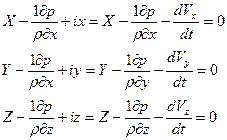
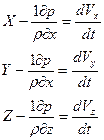
 .
.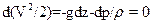 .
.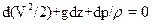 .
. .
. .
.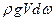 и проинтегрировав по площади живого сечения
и проинтегрировав по площади живого сечения  :
: .
. .
. .
.