Проблемы с квантовой теорией поля

Одним из ярких эпизодов поездки в Кембридж в 1994году был обед с моим старым другом сэром Роджером Пеироузом. Сэр Роджер как раз только что стал сэром Роджером, и мы с Энн приехали в Оксфорд поздравить его.

Все четверо — мы с Роджером и наши жены — сидели на берегу реки Червелл в приятном открытом ресторанчике, глядя на проплывающих мимо пантеров. Пантинг, если вы не знакомы с этим видом спорта, — это благородный способ катания на лодке с использованием длинного шеста для неспешного отталкивания им от дна. Это буколическое занятие всегда напоминает мне полотно Ренуара «Завтрак лодочников», но в нем есть свои опасности. Когда мимо проплывала лодка с группой поющих студентов, шест у симпатичной девушки, которая с ним управлялась, застрял в иле. Она не желала его отпускать и немало нас позабавила, когда продолжила цепляться за шест, глядя вслед уплывающей лодке.

Тем временем мы вчетвером делили заказанный на всех шоколадный мусс. Дамы уже прикончили свои порции, а мы с Роджеров смеясь над севшей на мель пантершей (она тоже хохотала), еще доедали оставшийся восхитительный темный шоколадный десерт. И тут мое внимание привлекло то, что мы с Роджером, вместо того чтобы брать шоколад полной вилкой, по очереди отрезаем половину от оставшегося куска. Роджер тоже это заметил, и началось соревнование — кто сможет последним разделить оставшийся кусочек.

Греки, напомнил Роджер, интересовались тем, бесконечно ли делима материя или у каждой субстанции есть свои мельчайшие неделимые кусочки — то, что они называли атомами. «Как ты думаешь, а существуют ли атомы шоколада?» — спросил я. Роджер заявил, что не припомнит, является ли шоколад одним из элементов периодической системы. Как бы то ни было, мы наконец доделили мусс до того, что казалось похожим на мельчайший атом шоколада, и, если я не ошибаюсь, он достался Роджеру. Инцидент с пантершей тоже счастливо завершился, когда мимо проплыла следующая лодка.

Проблема с квантовой теорией поля заключается в том, что пространство (и пространство-время) в ней подобны бесконечно делимому шоколадному муссу. Как бы тонко вы его ни нарезали, всегда можно разделить его еще тоньше. Все великие математические загадки имеют дело с бесконечностью. Как представить, что числа идут друг за другом без конца? Но как представить себе, что это не так? Как пространство может быть бесконечно делимым? Но как оно может таковым не быть? Я подозреваю, что бесконечность — главная причина помешательств среди математиков.

Помешанные или нет, математики называют бесконечно делимое пространство континуумом. Проблема с ним в том, что на самых малых расстояниях в нем может происходить ужасающее число событий. Фактически в континууме нет самого малого расстояния — вы можете сгинуть в процессе бесконечного спуска ко все меньшим и меньшим клеткам, и события будут происходить на каждом уровне. Иначе говоря, континуум может содержать бесконечное число битов информации в любом крошечном объеме пространства, сколь бы мал он ни был.

Проблема бесконечно малых особенно неприятна в квантовой механике, где все, что может дрожать, — дрожит, и «все, что не запрещено, обязательно». Даже в пустом пространстве при абсолютном нуле поля, такие как электрическое и магнитное, флуктуируют.

Эти флуктуации происходят во всех масштабах — от самых больших волн с длиной в миллиарды световых лет до волн размером не больше математической точки. Эта дрожь квантовых полей позволяет хранить неограниченное количество информации в любом крошечном объеме. И это рецепт математической катастрофы.

Потенциально бесконечное число битов в каждом крошечном объеме пространства проявляется на фейнмановских диаграммах как бесконечный переход ко все меньшим и меньшим субдиаграммам. Начнем с простой идеи пропагатора, изображающего электрон, движущийся из одной пространственно-временной точки в другую. Он начинается и заканчивается одним электроном.

Для электрона есть и другие способы попасть из точки а в точку b — например, жонглируя по пути фотонами.

Очевидно, что число таких возможностей бесконечно, а согласно фейнмановским правилам, все они должны быть просуммированы, чтобы определить вероятность. Каждую диаграмму можно украсить дополнительными структурами. Каждый пропагатор и узел можно заменить более сложной историей, включающей диаграммы внутри диаграмм внутри диаграмм, пока они не станут неразличимо мелкими. Но, пользуясь мощной лупой, можно добавлять еще более мелкие структуры, и так до бесконечности.

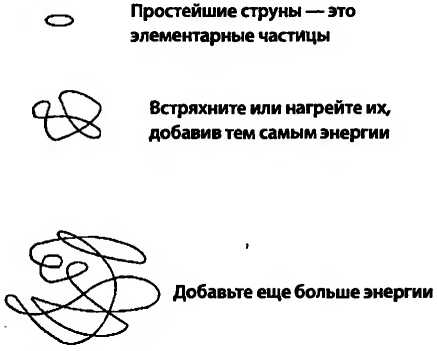
Возможность бесконечно добавлять на фейнмановские диаграммы все более мелкие структуры — одно из тревожных следствий континуальности пространства-времени в квантовой теории поля: количество шоколадного мусса всегда можно уменьшить.

С учетом всего этого — неудивительно, что квантовая теория поля математически опасный предмет. Непросто добиться, чтобы все флуктуации в бесконечно большом числе бесконечно малых ячеек пространства собрались в целостную вселенную. В действительности квантовая теория поля по большей части идет вразнос и дает бессмыслицу. Даже Стандартная модель элементарных частиц может при окончательном анализе не оказаться математически корректной.

Но ничто не сравнится с трудностями, возникающими, когда пробуешь построить квантовую теорию гравитации. Напомню, гравитация — это геометрия. При попытках совместить общую теорию относительности с квантовой механикой оказывается, что по правилам квантовой теории поля само пространство-время постоянно меняет свою форму. Если бы можно было рассмотреть под увеличением крошечную область пространства, мы увидели бы, что оно бешено дрожит, изгибаясь и образуя крошечные кочки и узлы кривизны. Более того, чем сильнее увеличение, тем неистовее становятся эти флуктуации.

Гипотетические фейнмановские диаграммы, включающие гравитоны, отражают эти извращения. Бесконечное число все меньших и меньших диаграмм вырывается из-под контроля. Каждая попытка придать смысл квантовой теории поля для гравитации приводила к одному и тому же результату: в самых малых масштабах происходит слишком много всего. Применение обычных методов квантовой теории поля к гравитации ведет к математическому фиаско.

У физиков есть способ обойти катастрофу, связанную с бесконечной делимостью пространства: они притворяются, будто пространство, подобно шоколадному муссу, не является истинным континуумом. Предполагается, что, дойдя в делении пространства до определенной точки, вы обнаружите у него неделимые крупицы, которые уже нельзя больше раздробить. Иными словами, они прекращают рисование фейнмановских диаграмм, когда их подструктуры становятся слишком маленькими. Это ограничение по малости величины называется перенормировкой. По сути, перенормировка — не что иное, как разбиение пространства на неделимые вокселы, вмещающие не более одного бита.

Перенормировка кажется уходом от проблемы, но для нее есть одно оправдание. Физики долго рассуждали о том, что планковская длина является предельно малым атомом пространства. Фейнмановские диаграммы, даже включающие гравитоны, сохраняют четкий смысл, если только прекратить добавлять к ним структуры меньше планковского размера или около того. Поэтому почти все ожидали, что пространство на планковском масштабе имеет неделимую, гранулярную, вокселизированную структуру.

Но это было до открытия голографического принципа. Как мы увидели в главе 18, замена непрерывного пространства массивом вокселов, имеющих конечный, планковский размер, — это ошибочная идея. Вокселизация пространства значительно завышает число вариантов заполнения его областей. Это привело бы Птолемея к ошибочному выводу относительно числа битов, которые могут храниться в его библиотеке, а теоретических физиков — к неверному представлению о количестве информации, которая может содержаться в области пространства.

Почти с самого появления теории струн признавалось, что она решает загадку бесконечно малых фейнмановских диаграмм. Отчасти она достигает этого, избавляясь от идеи бесконечно малых частиц. Но вплоть до появления голографического принципа недооценивалось, насколько радикально теория струн отличается от перенормировочной или вокселизированной версии квантовой теории поля. Замечательный факт состоит в том, что теория струн — это принципиально голографическая теория, описывающая пикселизированный мир.

Современная теория струн, как и ее более ранние воплощения, имеет дело с открытыми и замкнутыми струнами. В большинстве, хотя и не во всех, версий теории фотон — это открытая струна, подобная мезону, но только значительно меньше. Во всех версиях гравитон — это замкнутая струна, больше всего напоминающая миниатюрный глюбол. Может ли быть так, что в каком-то неожиданном глубоком смысле эти два типа струн — фундаментальные и КХД-струны — окажутся одними и теми же объектами? С учетом различия в их размерах это кажется маловероятным, однако струнные теоретики стали подозревать, что это огромное различие в масштабах может вводить в заблуждение. В главе 23 мы увидим, что в теории струн есть определенное единство, но пока мы будем говорить о двух разных теориях струн для разных явлений.

Струна — это гибкий объект, длина которого много больше толщины: шнурок для ботинок или рыболовная леска — это струны. В физике слово «струна» также подразумевает эластичность: струны могут растягиваться и сжиматься, подобно жгуту эспандера или резиновой ленте. КХД-струны очень прочные — к концу мезона можно подвесить большой грузовик, но фундаментальные струны еще прочнее. На самом деле, невзирая на ничтожную толщину, фундаментальные струны так невероятно прочны, что в мире обычной материи их не с чем сравнить. Число грузовиков, которое могла бы выдержать фундаментальная струна, составляет около 1040. Из-за этого колоссального натяжения чрезвычайно трудно растянуть фундаментальную струну до сколько-нибудь заметных размеров. Поэтому типичные размеры фундаментальных струн должны быть ненамного больше планковской длины.

Для струн, с которыми мы сталкиваемся в повседневной жизни, — жгутов для эспандера, резиновых лент и растянутых жевательных резинок — квантовая механика особой роли не играет, но КХД-струны и фундаментальные струны — это существенным образом квантово-механические объекты. Среди прочего это означает, что энергия может добавляться им лишь дискретными, неделимыми порциями. Переход от одного значения энергии к другому может быть выполнен только «квантовым скачком» вверх по лестнице энергетических уровней.

Нижний конец энергетической лестницы называется нулевым состоянием. Добавление одной единицы энергии переводит в первое возбужденное состояние. Следующий энергетический шаг дает второе возбужденное состояние и так далее шаг за шагом. Обычные элементарные частицы, такие как электроны и фотоны, находятся внизу лестницы. Если они вообще вибрируют, это лишь квантовые нулевые колебания. Но если теория струн верна, то их можно заставить вращаться и колебаться со все большей энергией (а значит, и массой).

Гитарную струну можно возбудить, щипнув медиатором, но, как вы понимаете, гитарный медиатор великоват для того, чтобы возбудить электрон. Простейший способ состоит в том, чтобы ударить электрон другой частицей. В результате мы используем одни частицы в качестве «медиаторов», чтобы «щипать» другие. Если столкновение достаточно сильное, оно заставит обе струны вибрировать в возбужденных состояниях. Естественно задать вопрос: «Почему бы физикам-экспериментаторам не возбудить электроны и протоны на ускорителях, сняв тем самым, раз и навсегда, вопрос о том, являются ли частицы вибрирующими струнами?» Проблема в высоте ступеньки — она слишком велика. Энергия, необходимая для того, чтобы закрутить или заставить вибрировать адрон, — довольно умеренная по стандартам современной физики элементарных частиц, но энергия, требуемая для возбуждения фундаментальной струны, чрезмерно велика. Добавление электрону одной порции энергии увеличило бы его массу почти на планковскую величину. Еще хуже то, что эту энергию надо сконцентрировать в невероятно малом объеме пространства. Грубо говоря, потребовалось бы затолкать массу миллиарда миллиардов протонов в область размером в миллиард миллиардов раз меньше самого протона. Ни один из построенных ускорителей даже близко не подходит для такой задачи. Подобное никогда не делалось и, вероятно, никогда не будет сделано^[132].

Сильно возбужденные струны в среднем больше тех, что находятся в нулевом состоянии; дополнительная энергия растягивает их, увеличивая их длину. Если суметь вкачать в струну достаточную энергию, она растянется и станет похожа на большой, безумно дрожащий, запутанный клубок шерсти И тут нет предела; при наличии достаточной энергии струну можно растянуть до любого размера.

Есть только один способ, которым сильно возбужденные струны могут быть получены в природе, раз уж их не получить в лаборатории. Как мы увидим в главе 21, черные дыры — даже те гиганты, что находятся в центрах галактик, — это колоссальные запутанные «струны-монстры».

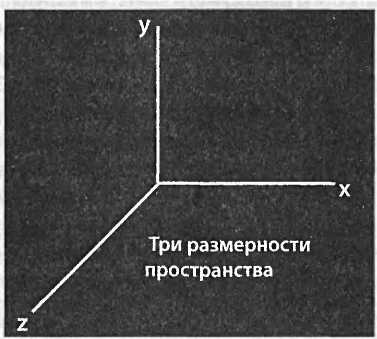
Существует еще одно важное и удивительное следствие квантовой механики, слишком тонкое и технически сложное, чтобы объяснять его здесь. Пространство, каким мы его обычно воспринимаем, трехмерно. Существует много терминов для описания этих трех измерений, например долгота, широта и возвышение или длина, ширина и высота. Математики и физики часто описывают размерности, используя три оси, обозначенные x,yw.z.

Однако фундаментальным струнам недостаточно для движения только трех измерений. Я имею в виду, что тонкая математика теории струн становится ненадежной, пока к пространству не добавляются дополнительные измерения. Струнные теоретики много лет назад обнаружили, что математическая согласованность их уравнений нарушается, если не ввести шесть дополнительных измерений пространства. Мне всегда казалось, что если понимаешь что-то достаточно хорошо, то должна быть возможность объяснить это неформально. Но потребность теории струн в шести дополнительных измерениях так и не поддается простому объяснению, хотя прошло уже тридцать пять лет. Боюсь, тут я вынужден буду прибегнуть к методу негодяев и сказать: «Можно показать, что…»

Я бы очень удивился, встретив кого-то, способного представить себе четыре или пять измерений, не говоря уже о девяти^[133]. Мне это удается не лучше, чем вам, но я могу добавить шесть букв алфавита — r, s, t, и, v, w — к обычным х, у и z, а затем терзать эти символы методами алгебры и анализа. При девяти измерениях, доступных для движения, «можно показать, что» теория струн становится математически согласованной.

Теперь вы можете спросить: если теория струн требует девяти измерений, а наблюдаемое пространство имеет только три, не является ли это прямым доказательством того, что теория струн неверна? Но не все так просто. Многие знаменитые физики, включая Эйнштейна, Вольфганга Паули, Феликса Клейна, Стивена Вайнберга, Мюррея Гелл-Манна и Стивена Хокинга (никто из них не является струнным теоретиком), серьезно рассматривали возможность того, что пространство имеет более трех измерений. Очевидно, они не галлюцинировали, значит, должен быть какой-то способ скрыть существование дополнительных размерностей. Характерные словечки, используемые для обозначения сокрытия дополнительных измерений, — «свертка» и «компактификация». Струнные теоретики сворачивают шесть дополнительных измерений посредством процесса, называемого компактификацией. Идея состоит в том, что дополнительные измерения пространства могут быть скручены в очень маленькие узлы, так что мы, огромные создания, слишком велики, чтобы в них перемещаться или даже заметить их.

Представление о том, что одно или более измерений можно скрутить в крошечную геометрическую форму, слишком маленькую, чтобы ее заметить, — это общее место современной физики высоких энергий. Некоторые люди думают, что дополнительные измерения — это слишком умозрительная идея, «научная фантастика с уравнениями», как сказал один остряк. Но это недопонимание, основанное на невежестве. Все современные теории элементарных частиц используют своего рода дополнительные размерности для обеспечения недостающих механизмов, которые делают частицы сложными.

Струнные теоретики не изобрели концепцию дополнительных измерений, а использовали ее особым творческим способом. Хотя теория струн требует шести дополнительных измерений, общее представление можно получить, добавив к пространству всего одно новое измерение. Давайте исследуем идею дополнительных измерений в этой ее простейшей ипостаси. Начав с мира, имеющего только одно пространственное измерение, — назовем его Лайнландией, — мы добавим одно дополнительное свернутое измерение. Для указания точки в Лайнландии достаточно всего одной координаты; обитатели называют ее X.

Чтобы Лайнландия стала интереснее, нам надо добавить в нее объекты, так что создадим частицы, которые движутся вдоль линии.

 

Думайте о них как о крошечных бусинах, которые сцепляются друг с другом, образуя одномерные атомы, молекулы и, возможно, даже живых существ. (Я сильно сомневаюсь, что жизнь может существовать в мире с одним измерением, но давайте пока подержим эти сомнения при себе.) Считайте и линию, и бусины бесконечно тонкими, так что они не высовываются в другие измерения. А лучше даже попытаться представить себе линию с бусинами вообще без других измерений^[134].

Сообразительный человек придумает много альтернативных версий Лайнландии. Все бусины могут быть одинаковыми, или, в более интересном мире, может существовать несколько разных типов бусин. Чтобы различать эти типы, пометим их цветами — красным, синим, зеленым и т. д. Я могу представить себе бесчисленно множество возможностей: красные бусины притягивают синие, но отталкивают зеленые. Черные бусины очень тяжелые, а белые — безмассовые и движутся по Лайнландии со скоростью света. Можно даже позволить бусинам быть квантово-механическими, цвет каждой отдельной бусины может быть неопределенным.

Жизнь в одном-единственном измерении очень стесненная. Имея свободу двигаться только вдоль одной линии, лайнландцы непременно будут сталкиваться друг с другом. Смогут ли они общаться? Легко: для отправки сообщений они могут перебрасываться бусинами, находящимися у их концов. Однако их социальная жизнь очень уныла: каждое существо имеет лишь двоих знакомых — одного справа и одного слева. Нужно по меньшей мере два измерения, чтобы сформировать социальный круг.

Но внешность обманчива. Когда лайнландцы смотрят в очень сильный микроскоп, они начинают обнаруживать, что их мир в действительности двумерный. Они видят не идеальную математическую линию нулевой толщины, а скорее поверхность цилиндра. В обычных обстоятельствах окружность этого цилиндра слишком мала, чтобы лайнландцы могли ее обнаружить, но под микроскопом удалось открыть куда более мелкие объекты, меньше даже, чем лайнландские атомы. Эти объекты столь малы, что могут двигаться в двух измерениях.

 

Подобно своим братьям-великанам, эти лайнландские карлики могут перемещаться вдоль цилиндра, но они достаточно малы, чтобы обходить по его окружности. Они способны даже двигаться одновременно по обоим направлениям, накручивая спиральные витки вокруг цилиндра. И — о, радость! — они могут даже обходить друг друга без столкновений. Вполне резонно они утверждают, что живут в двумерном пространстве, но с одной особенностью: если двигаться по прямой линии в дополнительном измерении, то скоро вернешься в исходную точку.

Лайнландцам понадобилось название для нового направления, и они обозначили его Y. В отличие от Х, вдоль Y нельзя далеко уйти, не вернувшись в исходную точку. Лайнландские математики говорят, что направление Y компактифицировано.

Цилиндр, изображенный выше, получается при добавлении дополнительного свернутого измерения к исходному одномерному миру. Добавление шести дополнительных измерений к миру, в котором уже есть три обычных, выходит далеко за пределы способностей человеческого мозга к визуализации. Физиков и математиков отличает от остальных людей не то, что они мутанты, способные представить себе любое число измерений, а скорее то, что они прошли тяжелую математическую переподготовку, опять же, перепрошивающую сознание, — чтобы научиться «видеть» дополнительные измерения.

Единственное дополнительное измерение не обеспечивает достаточного разнообразия возможностей. Перемещение в свернутом направлении будет подобно движению по кругу без осознания этого. Но уже два дополнительных измерения открывают бесконечное множество новых возможностей. Два измерения могут образовать сферу.

тор (поверхность бублика),

бублик с двумя или тремя дырками,

или даже причудливое пространство, называемое бутылкой Клейна.

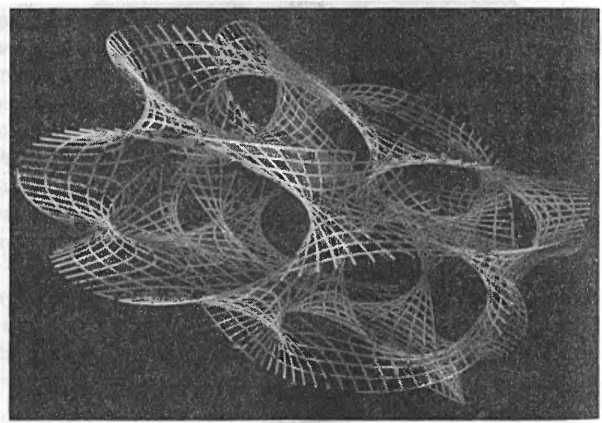
Изображение двух дополнительных измерений не составляет больших проблем (мы только что сделали это), но с ростом числа измерений визуализировать их становится все труднее и труднее. К тому моменту когда мы достигнем шести дополнительных измерений, необходимых для теории струн, визуализация без обращения к математике становится безнадежным делом. Особые геометрические пространства, которые струнные теоретики используют для компактификации шести дополнительных измерений, называются многообразиями Калаби — Яу. Их насчитываются миллионы, и среди них нет двух одинаковых. Многообразия Калаби — Яу исключительно сложны, с сотнями шестимерных дырок от бубликов и прочими невообразимыми кренделями. Тем не менее математики создают их изображения, нарезая на слои меньшей размерности, подобно диаграммам вложения^[135]. Вот изображение двумерного среза типичного пространства Калаби — Яу.

Я попробую дать вам некоторое представление о том, на что похоже обычное пространство, когда к каждой его точке добавлено шестимерное многообразие Калаби — Яу. Сначала посмотрите на обычные измерения, в которых могут двигаться такие большие объекты, как люди. (Я нарисовал его двумерным, но вы уже должны научиться достраивать третье измерение в воображении.)

В каждой точке трехмерного пространства имеется также шесть других свернутых измерений, в которых могут перемещаться очень маленькие объекты. По необходимости я рисую пространства Калаби — Яу отдельно друг от друга, но вы должны представлять себе их в каждой точке обычного пространства.

Теперь вернемся к струнам. Обычный жгут от эспандера можно растягивать в разных направлениях, например вдоль оси восток — запад, или север — юг, или верх — низ. Его можно растягивать под разными углами, скажем, на север-северо-запад с 10-градусным наклоном к горизонту. Но если есть дополнительные измерения, число возможностей многократно возрастает. В частности, струны Могут растягиваться вдоль свернутых измерений. Замкнутая струна Может опоясывать пространство Калаби — Яу один или несколько Раз, но при этом вовсе не быть растянутой в обычных пространственных направлениях.

Позвольте мне еще немного усложнить ситуацию. Струна может опоясывать свернутое пространство и в то же самое время извиваться, подобно змее, так что изгибы прокатываются по струне.

Чтобы натянуть струну вокруг свернутого измерения и заставить ее вибрировать, требуется энергия, так что частицы, описываемые такими струнами, будут тяжелее обычных.

Силы

Наша Вселенная — это мир не только пространства, времени и частиц, но также и сил. Электрические силы, действующие между заряженными частицами, могут перемещать кусочки бумаги и пылинки (скажем, за счет статического электричества), но более важно, что эти силы удерживают электроны на их орбитах вокруг атомных ядер. Гравитационные силы, действующие между Землей и Солнцем, удерживают на орбите Землю.

Все силы в конечном счете связаны с микроскопическими силами, действующими между отдельными частицами. Но откуда берутся эти межчастичные силы? Для Ньютона универсальная силапритяжения, действующая между массами, была просто физическим фактом — в действительности он смог ее только описать, но не объяснить. Однако в течение девятнадцатого и двадцатого столетий такие физики, как Майкл Фарадей, Джеймс Клерк Максвелл, Альберт Эйнштейн и Ричард Фейнман, сделали блестящие открытия, объяснявшие силы через стоящие за ними более фундаментальные концепции.

Согласно Фарадею и Максвеллу, электрические заряды притягиваются и отталкиваются не непосредственно; в пространстве между зарядами существует посредник, передающий взаимодействие. Представьте себе «Слинки» — эту ленивую игрушечную пружинку, — натянутую между двумя разнесенными на некоторое расстояние шарами.

Каждый из шаров подвергается воздействию силы только со стороны присоединенного к нему конца «Слинки». Затем каждый фрагмент «Слинки» воздействует на своих соседей. Сила передается по «Слинки», пока не передаст натяжение к объекту на другом конце. Может казаться, что два объекта притягиваются друг к другу, но это иллюзия, созданная посредничающей между ними «Слинки».

Когда доходит до электрически заряженных частиц, посредничающие агенты — это заполняющие пространство между ними электрическое и магнитное поля. Хотя они невидимы, эти поля совершенно реальны: это непрерывные невидимые возмущения пространства, которые переносят взаимодействия между зарядами.

Эйнштейн в своей теории гравитации пошел еще глубже. Массы искривляют геометрию пространства-времени в своей окрестности и благодаря этому искажают траектории других масс. Искажения геометрии тоже можно рассматривать как поля.