Гравитационное замедление часов

Что за свойство черных дыр превращает их в машины времени? Ответ кроется в вызываемых ими сильных искажениях геометрии пространства-времени. Эти искажения по-разному влияют на течение собственного времени вдоль мировых линий в зависимости от того, где эти линии проходят. Вдали от черной дыры ее влияние незначительно, и поток собственного времени почти не меняется. Но часы, висящие на тросе над самым горизонтом, будут значительно замедляться деформацией пространства-времени. Фактически замедлятся все часы, включая ваше сердцебиение, метаболизм и даже невидимое движение атомов. Вы совершенно этого не заметите, но, вернувшись на космическую станцию и сравнив свои часы с бортовым хронометром, обнаружите расхождение. На станции пройдет больше времени, чем по вашим часам.

На самом деле необязательно возвращаться на станцию, чтобы заметить влияние черной дыры на время. Если вы у горизонта и я на борту станции располагаем телескопами, то сможем наблюдать друг за другом. Я буду видеть вас и ваши часы как в замедленной съемке, а вы увидите меня ускоренным, как в старом кино про полицейских из Кистоуна^[38]. Это относительное замедление времени вблизи больших масс называют гравитационным красным смещением. Оно было открыто Эйнштейном как следствие общей теории относительности и отсутствует в ньютоновской теории тяготения, где все часы идут строго в одинаковом темпе.

Следующая пространственно-временная диаграмма иллюстрирует гравитационное красное смещение вблизи горизонта черной дыры. Объект слева — это черная дыра. Напоминаю, что на картинках, изображающих пространство-время, вертикальная ось соответствует времени. Серая поверхность — это горизонт, а вертикальные линии на разных расстояниях от горизонта представляют группу одинаковых неподвижных часов. Отметки на них отражают течение собственного времени вдоль мировых линий. В каких единицах — неважно; это могут быть секунды, наносекунды или годы. Чем ближе часы к горизонту черной дыры, тем медленнее выглядит их ход. Непосредственно на горизонте время полностью останавливается по отношению к часам, оставшимся вне черной дыры.

Гравитационное замедление часов случается и в не столь экзотических условиях, как вблизи горизонта черной дыры. Умеренную величину этот эффект имеет на поверхности Солнца. Атомы — это миниатюрные часы, электроны, снующие вокруг ядра, подобны стрелкам часов. При наблюдении с Земли атомы на Солнце выглядят немного заторможенными.

Утрата одновременности, парадокс близнецов, искривленное пространство-время, черные дыры и машины времени — так много далеких от повседневности, более чем фантастических идей, и все это надежно установленные несомненные концепции, с которыми согласны все физики. Чтобы понять новую физику пространства-времени, требуется весьма сложный инструментарий — дифференциальная геометрия и тензорное исчисление, метрики пространства-времени и дифференциальные формы. Но даже куда более трудный переход в зазеркальный квантовый мир не сравнится по концептуальной сложности с теми проблемами, которые ставят нас в тупик, когда мы пытаемся взаимно увязать общую теорию относительности и квантовую механику. В прошлом были времена, когда казалось, что квантовая механика не способна к сосуществованию с эйнштейновской теорией гравитации и будет отброшена. И возможно, кто-то скажет, что Битва при черной дыре была «войной, которая сделала мир безопасным для квантовой механики».

В следующей главе я возьмусь за донкихотскую в своей невозможности задачу объяснить квантовую механику, обходясь по возможности без уравнений. Подлинное средство для грокинга квантовой вселенной — это абстрактная математика: бесконечномерные пространства Гилберта, проекционные операторы, унитарные матрицы и множество других понятий, на изучение которых требуется несколько лет. Посмотрим, как мы справимся с этим всего на нескольких страницах.

4
«Эйнштейн, не говори Богу, что ему делать»

Поставив свою чашку чая, она неуверенно спросила: «А свет состоит из волн или из частиц?»

 

Около дома под деревом стоял накрытый стол, а за столом пили чай Мартовский Заяц и Болванщик, между ними крепко спала Мышь-Соня. Болванщик и Заяц облокотились на нее, словно на подушку, и разговаривали через ее голову. «Бедная Соня, — подумала Алиса. — Как ей, наверно, неудобно! Впрочем, она спит — значит, ей все равно»^[39].

На последнем уроке физики Алису кое-что глубоко озадачило и она надеялась, что новые знакомые помогут разобраться в запутанных вопросах. Поставив свою чашку чая, она неуверенно cnpocuлa: «А свет состоит из волн или из частиц?» — «Да, именно так», — ответил Сумасшедший Болванщик. Немного раздраженно Алиса переспросила в полный голос: «Так какой же ответ? Я повторю вопрос: свет — это частицы или волны?» — «Совершенно верно», — подтвердил Болванщик.

Приветствуем вас в павильоне смеха — в сумасшедшем, ненормальном, на голове стоящем мире квантовой механики, где правит неопределенность и ничто порождает осмысленные ощущения.

Ответ Алисе (что-то вроде)

Ньютон считал, что лучи света — это потоки крошечных частиц, что-то вроде маленьких пуль, выбрасываемых скорострельным пулеметом. Хотя эта теория была почти полностью ошибочной, он придумал удивительно толковые объяснения для многих свойств света. Но к 1865 году шотландский математик и физик Джеймс Клерк Максвелл бесповоротно разгромил ньютоновскую «пулевую» теорию. Максвелл доказывал, что свет состоит из волн — электромагнитных волн. Построения Максвелла целиком и полностью подтвердились и вскоре стали общепризнанной теорией.

Максвелл подчеркивал, что при движении электрических зарядов, например когда электроны колеблются в проводах, эти движения порождают волнообразные возмущения, во многом подобно тому, как движения пальца по поверхности лужи с водой порождают волны на ее поверхности.

Световые волны состоят из электрического и магнитного полей — тех же, что окружают электрически заряженные частицы, электрические токи в проводах и обычные магниты. Когда эти заряды и токи колеблются, они испускают волны, которые распространяются в пустом пространстве со скоростью света. И действительно, если пропустить луч света сквозь пару тонких щелей, то можно заметить отчетливый интерференционный узор, создаваемый перекрывающимися волнами.

Теория Максвелла даже объяснила, благодаря чему свет бывает разного цвета. Волны характеризуются своей длиной — расстоянием от одного гребня до другого. Вот две волны, у первой из них длина больше, чем у второй.

Представьте себе две волны, движущихся прямо перед вашим носом со скоростью света. По мере движения они колеблются от максимума к минимуму и обратно: чем короче волна, тем быстрее эти колебания. Число полных циклов (от максимума до минимума и снова до максимума) в секунду называется частотой, и она, очевидно, выше у коротких волн.

Когда свет попадает в глаз, различные частоты по-разному воздействуют на палочки и колбочки сетчатки. Сигнал передается в мозг, который говорит, что это красный, оранжевый, желтый, зеленый, голубой или фиолетовый цвет в зависимости от частоты (или длины волны). На красный конец спектра приходятся более длинные волны (более низкие частоты), чем на голубой или фиолетовый конец: длина волны красного света — около 700 нм^[40], а фиолетового — примерно вдвое меньше. Поскольку скорость света очень высока, частота его колебаний чудовищна. Голубой свет совершает квадриллион (1015) колебаний в секунду; красный свет колеблется примерно вдвое медленнее. Физики говорят, что частота голубого света составляет 1015 Гц.

Может ли длина волны света быть больше 700 или короче 400 нанометров? Да, но тогда он не называется светом; глаз нечувствителен к таким длинам волн. Ультрафиолетовые и рентгеновские лучи короче фиолетовых волн, а самые короткие из всех лучей называются гамма-излучением. С длинноволновой стороны мы имеем инфракрасное излучение, микроволны и радиоволны. Весь спектр, от гамма-лучей до радиоволн, называют электромагнитным излучением.

Так что, Алиса, ответ на твой вопрос состоит в том, что свет определенно состоит из волн.

Но подожди, не спеши. Между 1900 и 1905 годами очень неприятный сюрприз поколебал основания физики, и данный вопрос на двадцать лет вновь стал крайне запутанным. (Кто-то скажет, что он и сегодня таким остается запутанным.) Основываясь на работе Макса Планка, Эйнштейн полностью «опрокинул доминирующую парадигму». У нас нет времени и места рассказывать, как он к этому пришел, но в 1905 году Эйнштейн заключил, что свет состоит из частиц, которые он называл квантами. Позже их стали называть фотонами. Сократим эту замечательную историю до голых фактов: свет, когда он чрезвычайно тускл, ведет себя как частицы, приходящие одна за другой, как если бы они были отдельными пулями. Вернемся к эксперименту, в котором свет проходит через две щели, а потом попадает на экран. Представьте себе затухающий источник излучения, который уже еле светит. Волновые теоретики будут ожидать появления очень тусклого волнообразного рисунка, едва видимого или даже вовсе неразличимого. Но видим он или нет, ожидаемый рисунок должен быть волнообразным.

Это не то, что предрекал Эйнштейн, а он, как обычно, был прав. Вместо непрерывного освещения его теория предсказывала отдельные точечные вспышки света. Первая вспышка появлялась в какой-то непредсказуемой точке экрана.

Следующая вспышка тоже возникала в случайном месте, следующая — снова. Если сфотографировать и наложить эти вспышки, то из случайных точек начинает складываться рисунок — волнообразный узор.

Так все же свет — частицы или волны? Ответ зависит от эксперимента и постановки вопроса. Бели эксперимент задействует столь слабый свет, что фотоны просачиваются буквально поштучно, то свет выглядит как приход случайных, непредсказуемых фотонов. Но если фотонов много, то они образуют рисунок: свет ведет себя подобно волнам. Великий физик Нильс Бор описывал эту странную ситуацию говоря, что волновая и корпускулярная теории света взаимно дополнительны.

Эйнштейн доказал, что фотоны должны обладать энергией. Тому есть убедительные свидетельства. Солнечный свет — фотоны, испущенные Солнцем, — согревают Землю. Солнечные батареи превращают фотоны, приходящие от Солнца, в электричество. Электричество может приводить в движение моторы и поднимать тяжелые грузы. Если свет обладает энергией, то это относится и к составляющим его фотонам.

Ясно, что отдельный фотон несет очень небольшое количество энергии, но сколько именно? Сколько нужно фотонов, чтобы вскипятить чашку чая или в течение часа крутить 100-ваттный мотор? Ответ зависит от длины волны излучения. Более длинноволновые фотоны менее энергичны, чем коротковолновые, так что их для выполнения работы потребуется больше. Очень знаменитая формула, — не настолько, конечно, как E = mc2, но все равно очень известная, — дает выражение для энергии отдельного фотона через его частоту^[41]:

Е = hf.

Стоящее в левой части уравнения Е представляет энергию фотона, выраженную в единицах, называемых джоулями. В правой части f — это частота. Для голубого света она составляет 1015 Гц. Оставшееся h — это знаменитая постоянная Планка, константа, которую Макс Планк ввел в 1900году. Постоянная Планка — очень маленькая величина, но это одна из самых важных фундаментальных констант, управляющая всеми квантовыми явлениями. Она стоит в одном ряду со скоростью света с и ньютоновской гравитационной постоянной G:

h = 6.62 x 10-34

Поскольку постоянная Планка очень мала, энергия отдельного кванта тоже ничтожна. Для вычисления энергии кванта голубого света умножаем постоянную Планка на частоту 1015 Гц и получаем 6,62x10-19 джоуля. Значит, потребуется 1039 голубых фотонов для того, чтобы вскипятить чашку чая. А фотонов красного света понадобится вдвое больше. Для сравнения: самых энергичных когда-либо зарегистрированных гамма-квантов на кипячение той же чашки ушло бы всего 1018 штук.

Приводя все эти формулы и числа, я хочу, чтобы вы запомнили только одну вещь: чем короче длина волны, тем выше энергия отдельного фотона. Высокая энергия означает короткие волны, низкая энергия — длинные волны. Повторите это несколько раз и запишите. И еще раз повторите: высокая энергия — короткие волны, низкая энергия — длинные волны.

Предсказание будущего?

Эйнштейн торжественно заявлял: «Бог не играет в кости»^[42]. Нильс Бор остроумно съязвил: «Эйнштейн, не говори Богу, что ему делать». Оба физика были очень близки к атеизму; крайне сомнительно; чтобы кто-либо из них имел в виду божество, восседающее на облаке и пытающееся выбросить семерку^[43]. Но оба, и Бор и Эйнштейн, пробивались через нечто совершенно новое в физике — нечто такое, что Эйнштейн просто отказывался принять: непредсказуемость, которую подразумевали странные новые квантово-механические законы. Разум Эйнштейна восставал против идеи случайности, против элемента непредсказуемости в законах природы. Мысль о том, что приход фотона — это принципиально непредсказуемое событие, была ему глубоко не по душе. Бор, напротив, принимал эту идею, нравилась она ему или нет. Он также понимал, что будущие физики сумеют «настроиться» на квантовую механику и эта настройка будет охватывать непредсказуемость, которой так боялся Эйнштейн.

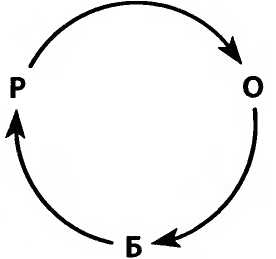
Нельзя сказать, что Бор лучше представлял себе квантовые явления или чувствовал себя с ними комфортнее. «Всякий, кто не был шокирован квантовой теорий, просто ее не понял», — сказал он однажды. Много лет спустя Ричард Фейнман заявил: «Я смело могу сказать, что квантовой механики никто не понимает»^[44]. И добавил: «Чем больше вы наблюдаете странное поведение Природы, тем сложнее построить модель, объясняющую даже простейшие явления. И теоретическая физика отказалась от этого»^[45]. Не думаю, что Фейнман действительно считал, что физики должны отказаться от попыток объяснить квантовые явления; в конце концов, он ведь сам их все время объяснял. Он имел в виду, что никто не может объяснить квантовые явления в терминах, которые человеческий мозг способен визуализировать при стандартной его «настройке». Фейнман не меньше других обращался к абстрактной математике. Очевидно, что чтение одной главы из книги без уравнений не может вас «перенастроить», но я все же надеюсь, что вы сумеете ухватить главные моменты.

Первое, от чего физики освободились и за что изо всех сил держался Эйнштейн, было представление о том, что физические законы детерминистичны. Детерминизм означает, что будущее можно предсказать, если достаточно много известно о настоящем. Ньютоновская механика, как и вся последующая физика, касалась предсказания будущего. Пьер Симон де Лаплас — тот самый Лаплас, что придумал темные звезды, — твердо верил в предсказуемость будущего. Вот что он писал:

Состояние Вселенной в данный момент можно рассматривать как следствие ее прошлого и как причину ее будущего. Мыслящее существо, которое в определенный момент знало бы все движущие силы природы и все положения всех объектов, из которых состоит мир, могло бы — если бы его разум был достаточно обширен для того, чтобы проанализировать все эти данные, — выразить одним уравнением движение и самых больших тел во Вселенной, и мельчайших атомов; для такого интеллекта не осталось бы никакой неопределенности, и будущее открылось бы перед его взором точно так же, как и прошлое.

Лаплас попросту выводил следствия из ньютоновских законов движения. Фактически мировоззрение Ньютона — Лапласа — это чистейшая форма детерминизма. Все, что вам нужно для предсказания будущего, — это знать положения и скорости всех частиц во Вселенной в некоторый начальный момент времени. Да, и, конечно, вам надо знать силы, действующие на каждую частицу. Знание положения частицы ничего не говорит о том, куда она направляется. Но если вы знаете ее скорость^[46] (как по величине, так и по направлению), вы можете сказать, где она окажется в следующий момент. Физики называют начальными условиями все то, что вам нужно одномоментно знать для предсказания будущего движения системы.

Чтобы понять, что означает детерминизм, давайте вообразим простейший возможный мир — столь простой, что у него есть всего два состояния бытия. Монетка — неплохая его модель, у нее есть два состояния — орел и решка. Нам также нужно задать закон, предписывающий, как состояния меняются от одного мгновения к следующему. Вот пара возможных таких законов.

♦ Первый пример очень скучный. Закон: ничего не происходит. Если в один момент монета лежит решкой вверх, то она будет лежать так же и в следующий момент (скажем, через наносекунду). Аналогично, если она лежит орлом, то будет так лежать и в следующий момент Этот закон сжато записывается парой простых «формул»:

Р → Р О → О

История мира будет бесконечным повторением: либо P P P Р Р…, либо О О О О О…

♦ Если первый закон совсем скучен, то второй лишь ненамного менее: каково бы ни было состояние в один момент, спустя наносекунду оно меняется на противоположное. Символически это можно выразить так:

P → O O → P

История примет тогда вид: PОPОPОРО… или ОPОPОРОР…

Оба этих правила детерминистичны, то есть будущее полностью определяется стартовой точкой. В любом случае, если знать начальные условия, можно с уверенностью предсказать, что случится спустя определенный отрезок времени.

Детерминистские законы — не единственно возможные. Могут быть и случайные законы. Простейшим случайным законом был бы такой, по которому независимо от начального состояния в следующий момент произвольно выпадает орел или решка. История, начинающаяся с орла, могла бы выглядеть так: ОООРРРООРР ΟΡΡΟ О… Но история ООРОРРОРРРО О… тоже вполне возможна. Фактически допустима любая последовательность. Можно считать это миром без законов или миром, закон которого предписывает случайное изменение начального состояния.

Но закон не обязан быть чисто детерминистичным или чисто случайным. Это крайности. Возможен закон, который в основном детерминистичен и содержит лишь малую долю случайности. Закон может, например, говорить, что с вероятностью девять десятых состояние сохраняется, а с вероятностью одна десятая — меняется на противоположное. Типичная история будет выглядеть так:

РРРРРРРООООООООООООРРРРРРРРРРРРРООООО…

В этом случае игрок с высокой вероятностью может предсказать, близкое будущее: следующее состояние, скорее всего, будет таким же, как и текущее. Шансы угадать будут высокими, если только не заглядывать слишком далеко вперед. Если попытаться предсказывать слишком далекое будущее, вероятности угадать и ошибиться оказываются почти равными. Эта непредсказуемость — как раз то, против чего выступал Эйнштейн, когда говорил, что Бог не играет в кости.

Один момент может вас несколько озадачить: последовательность бросков реальной монеты гораздо ближе к совершенно случайному закону, чем к любому из детерминистических. Случайность кажется очень распространенным свойством нашего мира. Почему понадобилась квантовая механика — чтобы внести в мир непредсказуемость? Но суждение о том, что падение монеты непредсказуемо, — даже без всякой квантовой механики — это чистой воды недоразумение. Проследить за всеми важными деталями обычно очень трудно. Монета — это все же не изолированный мир. Тонкости движения мышц, которые двигают руку и подбрасывают монету; потоки воздуха в комнате; тепловые колебания молекул, как в самой монете, так и в воздухе, — все это факторы, влияющие на исход, и в большинстве случаев этой информации слишком много, чтобы с ней можно было работать. Помните, Лаплас говорил о существе, которое знает «все движущие силы природы и все положения всех объектов, из которых состоит мир»? Малейшей ошибки в положении единственной молекулы достаточно для того, чтобы разрушить способность предсказания будущего. Но не этот обыденный вид случайности беспокоил Эйнштейна. Под Богом, играющим в кости, Эйнштейн подразумевал то, что глубочайшие законы природы содержат неустранимый элемент случайности, который никак нельзя обойти, даже если нам известно всё, что в принципе можно узнать.

Информация не умрет никогда

Один непреодолимой силы аргумент против того, чтобы допускать случайность, состоит в том, что в большинстве случаев она будет нарушать закон сохранения энергии (см. главу 7). Этот закон утверждает, что, хотя энергия может существовать во множестве разных форм и способна переходить из одной формы в другую, полное количество энергии никогда не меняется. Сохранение энергии — один из наиболее тщательно подтвержденных фактов относительно природы, и возможностей перехитрить его совсем немного. Случайные толчки будут изменять энергию объекта, спонтанно его ускоряя или тормозя.

Существует другой, очень тонкий физический закон, который, возможно, даже более фундаментален, чем закон сохранения энергии. Его иногда называют обратимостью, но давайте будем называть его законом сохранения информации. Сохранение информации подразумевает, что если вы с идеальной точностью знаете настоящее, вы можете предсказать будущее на все времена. Но это лишь половина дела. Закон также утверждает, что если вы знаете настоящее, то вы можете быть абсолютно уверены в прошлом. То есть он работает в обоих направлениях.

В мире орлов и решек одной монеты полностью детерминистический закон гарантирует идеальное сохранение информации. Например, при законе

P → O O → P

как прошлое, так и будущее можно предсказать идеально точно. Но даже малейшая доля случайности разрушает эту идеальную предсказуемость.

Давайте рассмотрим другой пример, на этот раз с воображаемой трехсторонней монетой (игральная кость — это шестисторонняя монета). Назовем три стороны орлом, решкой и ребром или О, Р и Б. Вот идеально детерминистический закон:

P → O O → Б Б → P

Чтобы визуализировать его, полезно нарисовать диаграмму.

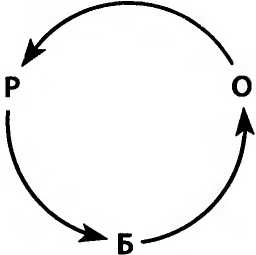
С таким законом история мира, начинающаяся с Р, будет выглядеть так:

РОБРОБРОБРОБРОБРОБРОБРОБ…

Существует ли способ экспериментально проверить закон сохранения информации? Фактически есть множество способов, одни из них реализуемы, другие нет. Если вы способны контролировать закон и менять его по своему желанию, выполнить проверку будет очень просто. Вот как это сделать в случае трехсторонней монеты. Начнем с одного из трех ее состояний, и пусть определенное время все идет своим чередом. Допустим, каждую наносекунду состояние меняется с Р на О, затем на Б и далее в цикле по всем трем возможностям. В конце отмеренного интервала времени изменим закон. Новый закон будет таким же, как прежний, но с обратным порядком обхода — не по часовой стрелке, а против.

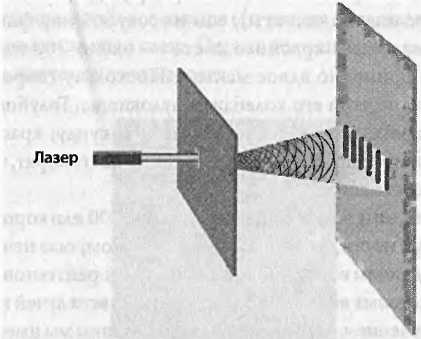
Теперь дадим системе поработать на обратном ходу ровно столько же времени, сколько она работала на прямом. Первоначальная история повернется вспять, и монета вернется в исходную точку. Не важно, сколько времени вы ждали, детерминистический закон обладает идеальной памятью и всегда возвращает к начальным условиям. Чтобы проверить закон сохранения информации, вам даже не надо знать точный вид этого закона, главное, чтобы он был обратимым. Данный эксперимент удается всегда, если только закон детерминистичен. Но он окончится неудачей, если имеет место какая-либо случайность (если только эта случайность не совсем уж ничтожная).

Вернемся к Эйнштейну, Бору, Богу (воспринимайте его как законы физики) и квантовой механике. Еще один знаменитый афоризм Эйнштейна гласит: «Господь изощрен, но не злонамерен». Я не знаю, что заставило Эйнштейна думать, что законы физики не злонамеренны. Лично я порой нахожу, что закон тяготения — весьма злая штука. Но Эйнштейн был прав относительно изощренности. Законы квантовой механики крайне изощренны — настолько изощренны, что они позволяют случайности сосуществовать как с законом сохранения энергии, так и с сохранением информации.

Рассмотрим частицу. Подойдет любая, но лучше выбрать фотон. Он порождается источником света, лазером например, и направляется к непрозрачному листу металла с крошечным отверстием в нем. За отверстием находится люминесцентный экран, который вспыхивает, когда на него попадает фотон.

Через некоторое время фотон может пройти через отверстие или промахнуться и отразиться от препятствия. В первом случае он попадает на экран, но не обязательно напротив отверстия. Вместо сохранения прямолинейного движения фотон может, проходя через отверстие, приобрести случайный импульс. Так что окончательное положение вспышки непредсказуемо.

Теперь удалим люминесцентный экран и повторим эксперимент. Через короткое время фотон либо попадет в металлический лист и отразится, либо пройдет через отверстие, испытав случайный толчок. Не имея ничего для детектирования фотона, невозможно сказать, где находится фотон и в каком направлении он движется.

Но представим, что мы вмешались и обратили закон движения фотона^[47]. Чего ждать от такого реверсированного фотона спустя тот же отрезок времени? Естественно ожидать, что случайность (при развороте случайность остается случайностью) похоронит всякую надежду на то, что фотон вернется в исходную точку. Случайность второй половины нашего эксперимента должна наложиться на случайность первой половины и сделать движение фотона еще более непредсказуемым.

Однако ответ куда изощреннее. Прежде чем я объясню, в чем дело, давайте ненадолго вернемся к эксперименту с трехсторонней монетой. 1 км мы тоже сначала запускали закон в одном направлении, а потом обращали его. В том эксперименте была одна деталь, которую я опустил: смотрел ли кто-нибудь на монету непосредственно перед тем, как обратить закон. Но что может измениться, если кто-то подсматривал? Ничего не изменится, если только взгляд на монету не меняет ее состояния. Кажется, это не слишком жесткое условие; хотел бы я посмотреть на монету, которая подлетает в воздух и переворачивается только потому, что кто-то на нее посмотрел. Но в изысканном мире квантовой механики нельзя взглянуть на кого-то, не побеспокоив.

Возьмем фотон. Когда мы запускаем его в обратном направлении, возвращается ли он в свое исходное положение, или же случайность квантовой механики подрывает сохранение информации? Ответ оказывается довольно странным: все зависит от того, смотрели ли мы на фотон в момент нашего вмешательства. Под словами «смотреть на фотон» я подразумеваю проверку местоположения или направления движения фотона. Бели мы подсматриваем, то конечный результат (после обратного прогона) будет случайным и закон сохранения информации нарушится. Но если мы проигнорируем фотон, не предприняв абсолютно ничего для определения его положения и направления движения, а просто обратим закон, фотон спустя предписанный отрезок времени магическим образом вернется в свое исходное положение. Иными словами, квантовая механика, несмотря на свою непредсказуемость, тем не менее подчиняется закону сохранения информации. Не знаю, злонамерен Бог или нет, но он, безусловно, изощрен.

Обращение вспять физических законов вполне осуществимо математически. А что можно сказать о реальности? Я очень сильно сомневаюсь, что кто-то сможет когда-нибудь обратить сколько-нибудь нетривиальную систему. Тем не менее, можем мы выполнить это на практике или нет, математическая обратимость квантовой механики (физики говорят о ее унитарности) критически важна для ее целостности. Без этого квантовая логика разрушается.

Тогда почему Хокинг думал, что информация уничтожается при объединении квантовой теории с гравитацией? Если сжать аргументацию до формата лозунга, он будет звучать так:

Информация, упавшая в черную дыру, — это утраченная информация.

Если выразить это иначе: законы никогда не могут быть обращены, поскольку ничто не может вернуться назад из-за горизонта черной дыры.

Если Хокинг был прав, то в законах природы будет содержаться все нарастающий элемент случайности и всё основание физики обрушится. Но к этому мы вернемся позже.

Принцип неопределенности

Лаплас считал, что он может предсказать будущее, если только достаточно знает о настоящем. К несчастью для всех будущих предсказателей мира, узнать одновременно положение и скорость объекта невозможно. Я не о том, что это чрезвычайно трудно или что неосуществимо при современном уровне развития технологии. Никакая технология, подчиняющаяся законам физики, никогда не сможет справиться с этой задачей, точно так же как ни одна технология не позволит перемещаться быстрее света. Любой эксперимент, поставленный так, чтобы одновременно измерять положение и скорость частицы, пойдет против принципа неопределенности Гейзенберга.

Принцип неопределенности стал тем перевалом, который поделил физику на доквантовую классическую эпоху и постмодернистскую эру квантовых «странностей». Классическая физика охватывает все, что появилось до квантовой механики, включая ньютоновскую теорию движения, максвелловскую теорию света и эйнштейновскую теорию относительности. Классическая физика детерминистична; квантовая физика полна неопределенности.

Принцип неопределенности — это странное и дерзкое утверждение, сделанное в 1927 году 26-летним Вернером Гейзенбергом, после того как он и Эрвин Шрёдингер открыли математику квантовой механики. Даже в эпоху множества необычных идей этот принцип выглядит крайне странным. Гейзенберг не утверждал, что есть какие-либо ограничения на точность, с которой можно измерить положение объекта. Координаты, задающие положение частицы в пространстве, можно определить с любой желаемой степенью точности. Он также не ставил пределов точности, с которой может быть измерена скорость объекта. Но он утверждал, что никакой эксперимент, как бы сложно и изобретательно он ни был поставлен, не может измерить положение и скорость одновременно. Это как если бы эйнштейновский Бог устроил бы все так, чтобы никто и никогда не мог предсказывать будущее.

Хотя принцип неопределенности посвящен расплывчатости, но в нем самом, парадоксальным образом, нет ничего расплывчатого. Неопределенность — это строгая концепция, включающая измерения вероятностей, интегральное исчисление и прочие математические изыски. Впрочем, перефразируя широко известное выражение, одна картинка стоит тысячи уравнений. Начнем с представления о распределении вероятностей. Пусть для очень большого числа частиц, скажем для триллиона, изучается их расположение вдоль горизонтальной оси, также называемой осью X. Первая частица оказалась в точке х = 1,3257, вторая —х = 0,9134 и т. д. Можно составить длинный список координат всех частиц. К сожалению, этот список займет около десяти миллионов книг вроде этой, и для большинства задач в нем не будет чего-то особенно интересного. Было бы куда информативнее получить статистический график, показывающий долю частиц, обнаруженных на каждом значении х. Этот график может выглядеть примерно так:

Один взгляд на этот график говорит нам, что большинство частиц находится вблизи точки х = 1. Для некоторых задач этого может хватить. Но достаточно чуть присмотреться, чтобы высказаться значительно точнее. Около 90 % частиц находятся между отметками х = 0 и х = 2. Если делать ставки на то, где окажется конкретная частица, то наибольшие шансы будут при х— 1, но неопределенность — математическая мера того, насколько «широка» кривая на графике, — составит около 2 единиц^[48]. Греческая буква дельта (Δ) служит стандартным математическим обозначением для неопределенности. В данном случае Ах означает неопределенность координаты х для рассматриваемых частиц.

Проделаем еще один мысленный эксперимент. Вместо измерения положений частиц будем измерять их скорости, считая их положительными для частиц, движущихся вправо, и отрицательными для тех, что движутся влево. На этот раз горизонтальная ось представляет скорость V.

 

 

Из графика видно, что большинство частиц движется влево, и можно также составить представление о разбросе скоростей Δν.

Принцип неопределенности говорит примерно следующее: любая попытка уменьшить неопределенность положения неизбежно будет приводить к увеличению неопределенности скорости. Например, можно целенаправленно выбрать только частицы в узком диапазоне значений х: скажем, между х = 0,9 и х = 1,1, отбросив все остальные. Для этого тщательно отобранного подмножества частиц неопределенность будет составлять всего 0,2, в десять раз меньше исходного Δ х. Можно надеяться таким способом обойти принцип неопределенности, но это не срабатывает.

Оказывается, если взять то же подмножество частиц и измерить их скорости, разброс их значений окажется значительно больше, чем в исходной выборке. Вы можете удивиться, почему так происходит, но, боюсь, это просто один из непостижимых квантовых фактов, которым нельзя дать классического объяснения. Это одна из тех вещей, о которых Фейнман говорил: «Теоретическая физика отказалась от этого».

При всей непостижимости, это экспериментальный факт: всякий раз, когда мы сокращаем Δ х, неизбежным следствием становится рост Δ v. И аналогично, все, что приводит к сокращению Δ v, вызывает увеличение Δ х. Чем сильнее мы стараемся зафиксировать положение частицы, тем неопределеннее мы делаем ее скорость, и наоборот.

Это было грубое описание идеи, но Гейзенберг смог выразить свой принцип неопределенности в более точной, количественной форме. Он утверждает, что произведение Δν, Δ х и массы частицы т всегда больше (>) постоянной Планка h.

m Δ v Δ x > h.

Посмотрим, как это работает. Предположим, что мы очень тщательно подготовили частицы, так что величина Δ х чрезвычайно мала. Это вынуждает неопределенность скорости Δν становиться достаточно большой, чтобы произведение было больше h. Чем меньше мы делаем Δ х, тем больше становится Δν.