
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение перемещений и напряжений при удареСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Скорость тела в момент удара определяется по известной формуле свободного падения
Эта скорость за очень короткий промежуток времени удара, исчисляемый тысячными или сотыми долями секунды, упадет до нуля. Рис. 10.2 Благодаря большой величине ускорения (замедле- ния) возникает значительная сила инерции, величиной которой и определяется действие удара. Однако теоретически трудно установить закон изменения скорости, а следовательно, и величину силы инерции. Здесь применяется другой путь, основанный на законе сохранения энергии и на следующих допущениях: 1. Напряжения при ударе не превосходят предела пропорциональности, так что закон Гука при ударе сохраняет свою силу. 2. Тела после удара не отделяются друг от друга. 3. Масса неподвижного стержня считается малой по сравнению с массой ударяющего тела, поэтому в расчет не принимается. 4. Потерей части энергии, перешедшей в теплоту и в энергию колебатель-ного движения соударяющихся тел, пренебрегаем. Приравняем работу падающего груза потенциальной энергии деформации стержня. Работа, совершаемая весом падающего груза, Потенциальная энергия деформации при сжатии равна
Из этих двух уравнений получаем или
Разделив все члены этого уравнения на ЕА, получим
Но Gl/EA=Dlcm – укорочение стержня от статически приложенной нагрузки G. Тогда Решив это квадратное уравнение относительно D l дин, получим
Оставляя знак «плюс» (решение со знаком «минус» перед радикалом противоречит физическому смыслу задачи), получаем окончательно
где Кдин – динамический коэффициент. Разделив обе части последнего уравнения на длину стержня и умножив на модуль упругости Е, перейдем на основании закона Гука от деформаций к напряжениям
Из этих формул видно, что величины динамического напряжения и перемещения зависят от величины статической деформации ударяемого тела. Чем больше статическая деформация (при прочих равных условиях), тем меньше динамические напряжения. Вот почему для смягчения удара применяют прокладки (резиновые, пружинные), дающие большие деформации. При сжимающем ударе во избежание продольного изгиба динамические напряжения не должны превосходить критических напряжений. Аналогичный вид имеют формулы и для случая поперечного (изгибающего) удара, только в том случае вместо D lcm следует принимать статический прогиб балки в месте удара – z ст, а вместо D lдин динамический прогиб – z дин.
Частные случаи
1. Если h = 0, т. е. имеет место внезапное приложение нагрузки, то из формул (10.1) и (10.2) получим D lдин = 2D lcт; sдин = 2 sст. При внезапном приложении нагрузки деформации и напряжения вдвое больше, чем при статическом действии той же нагрузки. 2. Если высота падения h значительно больше статической деформации D l cт, то для определения динамического коэффициента получим следующую приближенную формулу:
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 855; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 .
. , где
, где  – перемещение в точке удара, равное укорочению стержня.
– перемещение в точке удара, равное укорочению стержня. .
. ,
, .
. .
.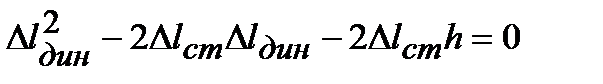 .
.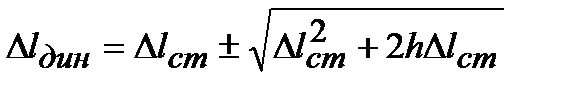 .
. , (10.1)
, (10.1)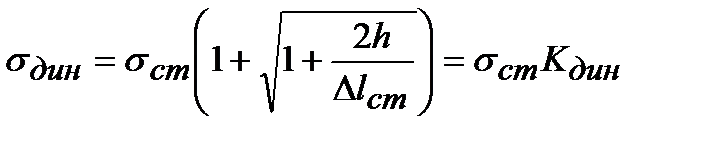 . (10.2)
. (10.2) .
.


