
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Путем интегрирования уравнения изогнутой оси балки
В этом случае неизвестными функциями, определяющими положение точек поперечных сечений балки, являются z (x) и j (x) = a (x) (рис. 7.1). Совокупность значений этих параметров по длине балки образуют две функции от координаты х - функцию перемещений z(х) и функцию углов поворота j (х). Из геометрических построений (рис. 7.1) наглядно видно, что угол наклона касательной к оси х и угол поворота поперечных сечений при произвольном х равны между собой. В силу малости углов поворота можно записать
Из курса математического анализа известно, что кривизна плоской кривой z(х) выражается следующей формулой:
Однако в связи с малостью величины
Учитывая выражение, полученное в предыдущей лекции,
где Iу - момент инерции поперечного сечения балки относительно ее нейтральной оси; Е - модуль упругости материала; E Iу - изгибная жесткость балки. Уравнение (7.3), строго говоря, справедливо для случая чистого изгиба балки, т.е. когда изгибающий момент Mу (х) имеет постоянное значение, а поперечная сила равна нулю. Однако это уравнение используется и в случае поперечного изгиба, что равносильно пренебрежению искривлениями поперечных сечений за счет сдвигов на основании гипотезы плоских сечений. Введем еще одно упрощение, связанное с углом поворота поперечного сечения. Если изогнутая ось балки является достаточно пологой кривой, то углы поворота сечений с высокой степенью точности можно принимать равными первой производной от прогибов. Отсюда следует, что прогиб балки принимает экстремальные значения в тех сечениях, где поворот равен нулю. В общем случае, для того чтобы найти функции прогибов z(х) и углов поворота j (х), необходимо решить уравнение (7.3) с учетом граничных условий между смежными участками. Для балки, имеющей несколько участков, определение формы упругой линии является достаточно сложной задачей. Уравнение (7.3), записанное для каждого участка, после интегрирования содержит две произвольные постоянные. На границах соседних участков прогибы и углы поворота являются непрерывными функциями. Данное обстоятельство позволяет определить необходимое число граничных условий для вычисления произвольных постоянных интегрирования.
Если балка имеет n - конечное число участков, из 2 n числа граничных условий получим 2 n алгебраических уравнений относительно 2 n постоянных интегрирования. Если момент и жесткость являются непрерывными по всей длине балки функциями Mу (х) и E Iу (х), то решение может быть получено как результат последовательного интегрирования уравнения (7.3) по всей длине балки: интегрируя один раз, получаем закон изменения углов поворота:
интегрируя еще раз, получаем функцию прогибов:
Здесь C 1 и С 2 – произвольные постоянные интегрирования – должны быть определены из граничных условий. Если балка имеет постоянное поперечное сечение по длине, то для определения функций прогибов и углов поворота удобно применить метод начальных параметров.
Метод начальных параметров
Метод начальных параметров получил широкое применение при решении различных инженерных задач. Его разработали советские ученые Н.П. Пузыревский, Н.К. Снитко, Н.И. Безухое, А.А. Уманский и др. Для того чтобы сократить число неизвестных произвольных постоянных интегрирования до двух, необходимо обеспечить равенство соответствующих постоянных на всех участках балки. Это равенство будет соблюдаться, если в уравнениях моментов, углов поворота и прогибов при переходе от участка к участку повторяются все силовые факторы предыдущего участка, а вновь появляющиеся слагаемые обращаются в нуль на левых границах своих силовых участков. Для обеспечения этих условий при составлении дифференциальных уравнений упругой линии и их интегрировании должны соблюдаться следующие условия: 1. Начало координат (общее для всех силовых участков) выбирается на конце балки: - если есть заделка, то в заделке; - если на конце есть опора, то на опоре; - если на обоих концах консоли, то безразлично, на каком конце начало координат. 2. При составлении уравнения для конкретного сечения учитываются нагрузки, расположенные от начала координат до сечения; распределенная нагрузка q продолжается до сечения в соответствии с правилами Клебша. При наличии сосредоточенного момента М его значение представлять в виде произведения М(z - l)0, где l – расстояние от начала координат до сечения, в котором этот момент приложен.
3. При действии распределенной нагрузки, не доходящей до правого конца рассматриваемого участка, она продолжается до этого конца и одновременно уравновешивается противоположно направленной нагрузкой той же интенсивности («дополнительная» и «уравновешивающая» нагрузки показываются на рисунках штриховыми линиями). 4. Интегрировать уравнение на всех участках, не раскрывая скобок. Рассмотрим балку (рис. 7.2) с постоянным поперечным сечением, нагруженную взаимоуравновешенной системой положительных силовых факторов (т.е. вызывающих вертикальные перемещения сечений балки в положительном направлении оси z). Начало системы координат поместим на левом конце балки так, чтобы ось x проходила вдоль оси балки, а ось z была бы направлена вверх. На балку действуют: момент М, сосредоточенная сила F и равномерно распределенная на участке бруса нагрузка интенсивностью q (рис. 7.2).
Рис. 7.2 Задача заключается в том, чтобы выявить особенности, вносимые в уравнение упругой линии, различными типами внешних силовых факторов. Для этого составим выражение изгибающих моментов для каждого из пяти участков заданной системы.
Участок II (l 1 £ x £ l 2 ) My ( x ) = M. Участок III (l 2 £ x £ l 3 ) My ( x ) = M + F (x - l 2). Участок IV (l 3£ x £ l 4) My (z) = M + F (x - l 2) + Участок V (l 4 £ х £ l 5) Mу (х) = M + F (х - l 2) +
На участке V, где распределенная нагрузка отсутствует, при выводе выражения для изгибающего момента с целью сохранения рекуррентности формул для разных участков была приложена взаимоуравновешенная распределенная нагрузка. Для вывода обобщенного выражения изгибающего момента введем следующий оператор Mу (х) = M Подставляя (7.4) в (7.3) и дважды интегрируя, получим выражение для прогибов: E Iу z (x) = C 0 + C 1 x + - Постоянные интегрирования C 0 и C 1 по своей сути означают: C 0 = E Iy z (0), C 1 = и определяются из граничных условий на левом конце балки. Тогда формула для прогибов примет следующий окончательный вид: E Iy z (x) = E Iyz 0 + + Соответственно формула для углов поворотов сечений балки определяется из (7.7) простым дифференцированием: E Iy j (x) = – Как видно, для определения прогибов и углов поворота балок данным методом начальных параметров достаточно знание лишь значений прогиба z 0 , угла поворота j 0 в начале системы координат, т.е. так называемых начальных параметров. Поэтому данный метод и называется методом начальных параметров.
Пример расчета
Для стальной балки, изображенной на рис. 7.3, определить методом начальных параметров углы поворота сечения и прогиб в точке D. Модуль упругости Е = 2×108 кН/м2. Поперечное сечение балки - квадратное со стороной a = 0,2 м.
Рис. 7.3 Решение 1. Определение опорных реакций балки (рис. 7.3).
S M 0 =0, RB (b + c + e) - q ×(c + e)×[ b + 0,5×(c + e)] + M + P b = 0,
S MB =0, R 0 (b + c + e) - 0,5× q ×(c + e)2 - M + P ×(c + e) = 0,
Для проверки правильности определения опорных реакций составим уравнение равновесия сил по оси z: S z =0; R 0 + RB + F - q (c + e) = 7,86 + 14,14 + 8 - 10×3 = 30 - 30 = 0. Реакции найдены верно. 2. Применение метода начальных параметров. Используя метод начальных параметров, для рассматриваемой балки запишем:
Из условий закрепления балки при x = 0 имеем: z 0 = 0; М 0=0. Подставляя числовые значения, получим:
В данном выражении неизвестно j 0. Из условия закрепления балки при x = b + c + e имеем, что z = 0. Вычисляя прогиб на правом конце балки и приравнивая его к нулю, получим уравнение для определения j 0:
Отсюда E I j0 = -20,84 кН×м2. Теперь выражение для определения прогибов будет иметь вид:
Соответственно выражение для определения углов поворота будет:
С помощью этих выражений определяем zD и j D:
Вычисляем жесткость сечения (Е = 2×108 кН/м2):
Тогда окончательно
Перемещение точки D происходит вниз, а сечение поворачивается по часовой стрелке.
Вопросы для самопроверки
1. Какие перемещения получают поперечные сечения балок при прямом изгибе? 2. Запишите основное дифференциальное уравнение изогнутой оси балки. 3. Что называется жесткостью сечения при изгибе? 4. Как из основного (приближенного) дифференциального уравнения изогнутой оси балки получаются выражения углов поворота и прогибов ее сечений? 5. Из каких условий определяются постоянные интегрирования, входящие в уравнение углов поворота и прогибов сечений балки? 6. Запишите универсальное уравнение метода начальных параметров. 7. Перечислите основные параметры для использования метода начальных параметров. 8. Что надо сделать, если распределенная нагрузка не доходит до правого конца балки?
|
||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 514; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.74.54 (0.03 с.) |
 . (7.1)
. (7.1) .
. по сравнению с единицей последнее выражение можно существенно упростить, и тогда
по сравнению с единицей последнее выражение можно существенно упростить, и тогда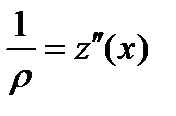 . (7.2)
. (7.2) , из (7.2) получим следующее важное дифференциальное соотношение:
, из (7.2) получим следующее важное дифференциальное соотношение: , (7.3)
, (7.3) ,
, .
.
 .
.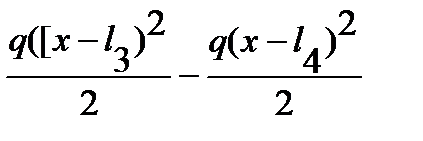 .
. , означающий, что члены выражения, стоящие перед ним, следует учитывать при х > li и игнорировать при х £ li. На основании этого обобщенное выражение момента Mу (х) для произвольного сечения х может быть записано единой формулой:
, означающий, что члены выражения, стоящие перед ним, следует учитывать при х > li и игнорировать при х £ li. На основании этого обобщенное выражение момента Mу (х) для произвольного сечения х может быть записано единой формулой: + F (х - l 2)
+ F (х - l 2)  +
+ 


 . (7.4)
. (7.4)
 +
+ 
 +
+ 
 -
-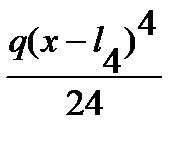
 . (7.5)
. (7.5)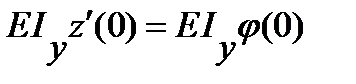 (7.6)
(7.6) x +
x + 
 +
+ 
 +
+
 -
- 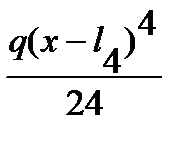
 . (7.7)
. (7.7) +
+ 
 +
+ 
 +
+ 
 -
-
 . (7.8)
. (7.8)

 кН;
кН; кН.
кН.


 .
. .
.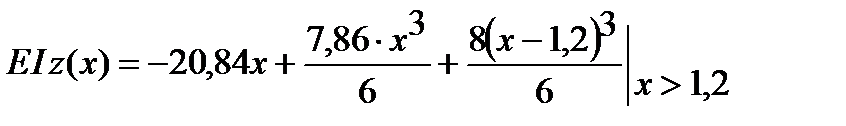
 .
.
 .
. кH×м3.
кH×м3. кН×м2.
кН×м2.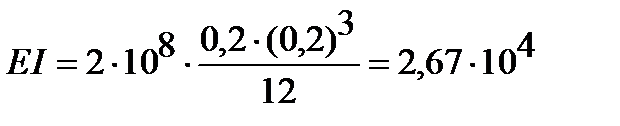 кН×м2.
кН×м2. м.
м. рад.
рад.


