Главные площадки и главные напряжения

 

Для того чтобы правильно оценить прочность бруса, необходимо уметь вычислять напряжение по любому сечению.

Через любую точку тела можно провести бесчисленное множество различно ориентированных площадок. При нагружении тела на этих площадках возникают в общем случае как нормальные, так и касательные напряжения.

Совокупность нормальных и касательных напряжений, возникающих на всем бесчисленном множестве площадок, которые можно провести через данную точку, характеризует напряженное состояние в этой точке.

Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по всем площадкам (сечениям), содержащим данную точку.

Исследование напряженного состояния дает возможность анализировать прочность материала для любого случая нагружения тела.

Пусть в окрестности исследуемой точки шестью попарно параллельными плоскостями выделен элементарный прямоугольный параллепипед с размерами ребер dx, dy и dz (рис. 3.1). По его граням будут действовать нормальные s_i и касательные t_ij напряжения. Обозначения нормальных напряжений содержат один индекс – наименование оси, которой параллельно данное напряжение. В обозначении касательных напряжений используются два индекса: первый совпадает с индексом нормального напряжения, действующее по данной площадке, а второй – наименование оси, которой параллельно данное касательное напряжение. Используем принятое правило знаков для напряжений. Нормальное напряжение σ считается положительным, если совпадает по направлению с внешней нормалью ` n к площадке, касательные напряжения t считаются положительными, если вектор касательных напряжений следует поворачивать против хода часовой стрелки до совпадения с внешней нормалью (рис. 3.2). Отрицательными считаются напряжения обратных направлений (рис. 3.3).

 

Рис. 3.2

s >0

t >0

s<0

t<0

`n

` n

Рис. 3.3

 

Рис. 3.1

 

 

Система сил, приложенных к элементарному кубу, должна удовлетворять условиям равновесия.

Рассмотрим элементарный параллелепипед размеров dx, dy, dz (рис. 3.1). Запишем уравнение равновесия параллелепипеда в виде суммы моментов относительно оси у (рис. 3.4), получим: .

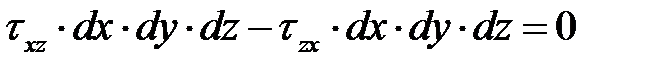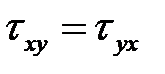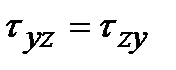Аналогично запишутся моменты сил относительно осей x и z. Из этих уравнений следует, что , , , т.е. на двух взаимно перпендикулярных площадках составляющие касательных напряжений, перпендикулярные к общему ребру, равны и направлены либо к ребру, либо от ребра. Этот вывод выражает закон парности касательных напряжений, который устанавливает зависимость между величинами и направлениями пар касательных напряжений, действующих по взаимно перпендикулярным площадкам элементарного параллелепипеда.

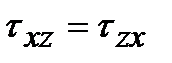Согласно закону парности касательных напряжений, знаки противоположны (рис. 3.4). Поэтому, если площадку с напряжением 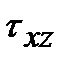поворачивать до совпадения с площадкой с напряжением 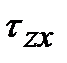, то обязательно найдется такое положение площадки, когда t = 0.

Площадки, по которым касательные напряжения равны нулю, называются главными, а действующие по этим площадкам нормальные напряжения – главными напряжениями.

Главные напряжения обозначаются s₁, s₂, s₃, причем s₁ ³ s₂ ³ s₃. Элемент, выделенный главными площадками, изображен на рис. 3.5.

 

tzx

txz

txz

tzx

s1

s2

s2

 

s3

s1

Рис. 3.5

Рис. 3.4

 

Виды напряженного состояния

 

В зависимости от количества действующих главных напряжений различают три вида напряженных состояний: линейное, плоское и объемное.