
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реальный объект и расчетная схемаСодержание книги
Поиск на нашем сайте Основные обозначения
А – площадь поперечного сечения, м2; N – продольная сила, кН; R – реактивная сила, кН; s – нормальное напряжение, МПа; Dl – абсолютная продольная деформация, мм; L – длина стержня, балки, м; e – относительная линейная деформация; n – коэффициент Пуассона; Е – модуль продольной упругости, МПа; U – потенциальная энергия деформации, Н×м; u – удельная потенциальная энергия деформации или перемещение вдоль оси х; р – полное напряжение, давление, МПа; q – погонная нагрузка, кН/м; F – сила (сосредоточенная), кН; g – удельный вес, кН/м3; G – модуль сдвига, МПа; [ s ] – допускаемое нормальное напряжение, МПа; [ s ] p, [ s ] c, [ s ] у – допускаемые нормальные напряжения соответственно на растяжение, сжатие, устойчивость, МПа; s – коэффициент запаса; sпч – предел прочности материала, МПа; sт – предел текучести материала, МПа; sпц – предел пропорциональности материала, МПа; r – плотность материала, кг/м3; gт – коэффициент надежности по материалу; gс – коэффициент условий работы; n – коэффициент перегрузки; Rt, Rc, Rs – расчетное сопротивление материала растяжению, сжатию, сдвигу, МПа; gk – коэффициент надежности, учитывающий степень ответственности и капитальности сооружения; t – касательное напряжение, МПа; q – угол поворота поперечного сечения балки, рад; относительное изменение объема элемента; Q – поперечная сила, кН; [ t ] – допускаемое касательное напряжение при сдвиге, МПа; sсм – напряжение смятия, МПа; [ sсм ] – допускаемое нормальное напряжение при смятии, МПа; А см – площадь смятия, м2; Sz, Sy – статистические моменты площади, м3; Iz, Iy – осевые моменты инерции сечения, м4; Ip – полярный момент инерции сечения, м4; Iyz – центробежный момент инерции сечения, м4; ус, zс – координаты центра тяжести сечения, м; Imax, Imin – главные моменты инерции сечения, м4; Wz, Wy – моменты сопротивления сечения, м3; Те – внешний скручивающий момент, Н×м; Mk – крутящий момент, Н×м; j – угол закручивания, рад; коэффициент уменьшения основного допускаемого напряжения; w – угловая скорость, рад/с; n – частота вращения, об/мин; Wр – полярный момент сопротивления, м3; [j] – допускаемый относительный угол закручивания, рад/м; m – внешний изгибающий момент, Н×м; М – внутренний изгибающий момент, Н×м; у – прогиб, вертикальное перемещение центра тяжести поперечного сечения балки; sэкв – эквивалентные напряжения, МПа; M экв –эквивалентный (расчетный) момент, МПа; F кр – критическая сила, кН; m – коэффициент приведения длины; l – гибкость стержня; lпред – предельная гибкость стержня; k д – динамический коэффициент; а – ускорение, м/с2; sа, tа –амплитуда цикла напряжений, МПа; sт –среднее напряжение цикла, МПа; R s – коэффициент асимметрии цикла; k d –коэффициент влияния абсолютных размеров сечения; ks, k t –эффективные коэффициенты концентрации напряжений; kF –коэффициент влияния шероховатости поверхности; kv –коэффициент влияния поверхностного упрочнения; ksD, kt D – коэффициенты снижения предела выносливости; ys, yt – коэффициенты чувствительности к асимметрии цикла.
Лекция 1. ОСНОВНЫЕ ПОНЯТИЯ И ИСХОДНЫЕ ПОЛОЖЕНИЯ
Вопросы лекции: 1. Введение. 2. Основные понятия и исходные положения. 3. Метод сечений, понятие о напряжениях. 4. Понятия о перемещениях и деформациях.
Введение
В процессе эксплуатации машин и сооружений их элементы (стержни, балки, пластины) в той или иной степени участвуют в работе конструкции и подвергаются воздействию различных нагрузок. Для обеспечения безаварийной работы конструкции инженеру необходимо подобрать материал и размеры конструктивных элементов таким образом, чтобы они: – не разрушались при действии расчетных нагрузок, т. е. были прочными; – были достаточно жесткими, т.е. перемещения (деформации) элементов конструкции не превышали заданных величин; – были устойчивыми, т.е. сохраняли под действием нагрузок первоначальную устойчивую форму равновесия. Сопротивление материалов – наука о прочности, жесткости и надежности элементов инженерных конструкций. Основная цель этой науки – дать методы подбора надежных размеров тел при наименьшем весе. В теоретической механике тело рассматривается как система материальных точек с неизменными расстояниями между ними. В природе таких абсолютно жестких тел не существует. Фактически при воздействии на тело внешних нагрузок расстояния между его частицами изменяются. Тело при этом меняет свои размеры и первоначальную геометрическую форму – деформируется. Внутренние силы, действующие между частицами, оказывают сопротивление внешним нагрузкам, приложенным к телу. Величина этого сопротивления зависит от степени деформации тела и физико-механических свойств материала, из которого оно изготовлено. Деформация тела продолжается до тех пор, пока не установится равновесие между конечными значениями внешних нагрузок и внутренними силами сопротивления. Полученное состояние тела будем называть напряженным состоянием. В дисциплине сопротивления материалов рассматриваются следующие основные вопросы: а) определение напряженного состояния деформируемых тел, вызванного силовыми воздействиями различного происхождения; б) анализ и обобщение результатов лабораторных опытов, проведенных над образцами из различного материала при различных силовых воздействиях; в) установление изменений размеров тел при деформациях; г) определение надежных размеров, при которых тело, не разрушаясь и не деформируясь свыше установленных норм, может длительно выдерживать заданные нагрузки при минимальном весе. При рассмотрении этих вопросов используется ряд основных понятий и определений. Введем основные понятия, принимаемые при изучении дисциплины. Прочность – это способность конструкции выдерживать заданную нагрузку, не разрушаясь. Жесткость – способность конструкции к деформированию в соответствии с заданным нормативным регламентом. Деформирование – свойство конструкции изменять свои геометрические размеры и форму под действием внешних сил. Устойчивость – свойство конструкции сохранять при действии внешних сил заданную форму равновесия. Упругость – способность тела восстанавливать свою форму после снятия внешних нагрузок. Пластичность – свойство тела сохранять полученную при нагружении деформацию после прекращения действия нагрузки. Ползучесть – способность материала медленно и непрерывно деформироваться при длительной постоянной нагрузке при высоких температурах. При этом главной задачей сопротивления материалов является формирование знаний для применения математического аппарата при решении прикладных задач, осмысления полученных численных результатов и поиска выбора наиболее оптимальных конструктивных решений. То есть данный предмет является базовым для формирования инженерного мышления и подготовки кадров высшей квалификации по техническим специализациям. В расчетах встречаются следующие три типа практических задач: 1) при заданных нагрузках найти размеры тела; 2) при заданных размерах тела установить допускаемые нагрузки; 3) при заданных нагрузках и размерах проверить тело на прочность, жесткость, устойчивость. Наука о сопротивлении материалов зародилась очень давно. Начало ее систематического развития можно отнести к 1638 г., когда вышла книга знаменитого итальянского ученого Галилея «Беседы и математические доказательства, касающиеся двух новых отраслей науки». Поводом к созданию этой книги послужил ряд практических вопросов, возникших при постройке судов, каналов и шлюзов в Венеции. В дальнейшем с ростом строительства и машиностроения развитие науки о сопротивлении материалов шло параллельно с развитием теоретической механики, что облегчило разработку основных законов и положений новой науки. Этому развитию способствовали работы выдающихся ученых и инженеров, среди которых видное место занимают ученые нашей страны. Следует указать на знаменитых ученых Л. Эйлера и Д. Бернулли, членов Петербургской академии наук, сделавших в XVIII в. большой вклад в развитие теории сопротивления материалов. В XIX в. были известны выдающиеся работы русских ученых: М. В. Остроградского, Д. И. Журавского, Ф. С. Ясинского и др., способствовавшие развитию теории упругих тел. В области испытания материалов надо отметить работы профессора Н. А. Белелюбского. С начала XX в. русские ученые играли видную роль в науке о сопротивлении материалов. Профессор И. Г. Бубнов создал теорию прочности корабля; академик А. Н. Крылов – крупнейший специалист по прикладной математике и механике – известен своими исследованиями динамических процессов; академик Б. Г. Галеркин решил ряд важных задач теории упругости и др. В России среди ученых, внесших ценный вклад в развитие теории сопротивления материалов и много сделавших для широкого применения ее к инженерным расчетам, следует назвать профессоров В. Л. Кирпичева, С. П. Тимошенко.
1.2. Основные понятия и исходные положения Основные гипотезы Внешние силы (нагрузки)
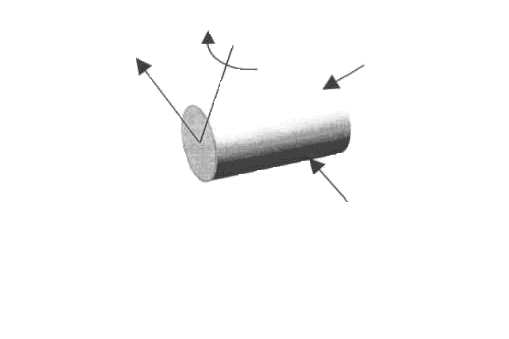
Внешними силами называются силы взаимодействия между рассматриваемым элементом конструкции и связанными с ним телами.Внешние силы еще принято называть нагрузками. Внешние силы (нагрузки), действующие на тело, по способу приложения разделяются на сосредоточенные, распределенные и объемные. Сосредоточенными называются такие нагрузки, которые прикладываются к небольшой площадке тела (размерность Н). Нагрузки, приложенные ко всей или какой-либо части поверхности тела, относятся к распределенным (размерность Н/м2). Эти нагрузки бывают равномерно распределенные, распределенные по треугольнику – треугольные и др. (рис. 1.3).
 
Рис. 1.3 Рис. 1.4
К первым относится, например, давление пара в котле, а ко вторым – давление воды на плотину. Нагрузки, распределенные по всему объему тела, называются объемными (размерность Н/м3). Примером такой нагрузки является собственный вес тела, силы инерции, магнитные силы.Нагрузки, распределенные по линии (рис. 1.4), называются погонными распределенными нагрузками (размерность Н/м). По характеру действия нагрузки разделяются на статические и динамические. Нагрузки, медленно возрастающие по времени от нуля до своего конечного значения, называются статическими (при расчетах силами инерции в этих случаях) здесь пренебрегают. Условие статического нагружения tнараст> где tнараст – время нарастания нагрузки; Т = w0– низшая частота. Динамические нагрузки сопровождаются значительными ускорениями точек деформируемого тела. При этом возникают силы инерции, которыми пренебречь нельзя. Динамические нагрузки делят на мгновенно приложенные, собственно ударные и повторно-переменные. Нагрузка считается мгновенно приложенной, или быстро приложенной, если она возрастает в течение короткого промежутка времени: tнараст< где Силами инерции вдоль оси Х пренебрегают, а в поперечном направлении (вдоль оси У) — их учитывают. При собственно ударном нагружении tнараст< Здесь силы инерции учитываются по всем направлениям координатных линий. В практике динамические нагрузки встречаются либо в чистом виде, либо в комбинации со статическими. Например, действие колеса локомотива на рельс выражается статической нагрузкой от собственного веса, сил инерции и ударной нагрузкой при прохождении рельсовых стыков.
Метод сечений Внутренние силы
Между соседними частицами тела (кристаллами, молекулами, атомами) всегда действуют силы сцепления – внутренние силы. Эти силы стремятся сохранить тело как единое целое. Они препятствуют всякой попытке деформировать тело. Величина этих сил при нагружении тела и в ненагруженном его состоянии будет различной. В сопротивлении материалов не рассматривают начальные внутренние силы в теле (в ненагруженном состоянии), а изучают дополнительные внутренние силы, которые появляются в результате нагружения тела. Внутренние силы часто называются усилиями. Для решения задачи о прочности надо уметь определять внутренние силы. Для этого в сопротивлении материалов широко применяют метод сечений. Сущность метода заключается в следующем. Пусть некоторое тело находится в равновесии под действием системы внешних сил (рис. 1.5 а). Рассечем (мысленно) тело на две части плоскостью, перпендикулярной продольной оси тела (поперечным сечением). Отбросим правую или левую часть тела. Чтобы оставшаяся часть находилась в равновесии, по плоскости сечения должны действовать внутренние силы. Заменим действие одной части на другую внутренними силами (рис. 1.5 б). Эти внутренние силы по характеру приложения – распределенные, в общем случае они не одинаковы по всему сечению. Внутренние силы могут быть приведены к их равнодействующим: главному вектору R и главному моменту М. Введем ортогональную систему координат с началом в точке О,причем ось Х пусть совпадает с продольной осью тела, а оси Y и Z – с главными центральными осями инерции поперечного сечения (о них будет сказано ниже). Разложим главный вектор R и момент М по осям (рис. 1.6). Получим шесть составляющих, которые называются внутренними силовыми факторами (ВСФ): N –продольная (нормальная) сила, проекция вектора R на ось X; Qz, Qy –поперечные силы, проекции вектора R на оси Z и Y соответственно; Мх = Мк – крутящий момент, составляющая момента М вокруг оси X; Mz, My – изгибающие моменты, составляющие момента М вокруг осей Z и Y соответственно.

а б
Рис. 1.5
Рассмотрим правую часть.
Рис. 1.6
Уравновесим отсеченную часть. Так как отсеченная часть тела находится в равновесии, то для определения шести неизвестных ВСФ. составим шесть уравнений статического равновесия:
из которых поочередно определяются все ВСФ: N = вующих на отсеченную часть, на продольную ось X; Qy = ций всех внешних сил, действующих на отсеченную часть, на оси У и Z соответственно; Mк = на отсеченную часть, относительно оси Х; Mу = тов, действующих на отсеченную часть, относительно осей Y и Z соответственно. Для наглядного представления о характере работы конструкции строят графики изменения ВСФ по длине бруса (вдоль оси Х). Такой график принято называть эпюрой (от французского слова ерuге-чертеж).
Понятие о напряжениях
Внутренние силы, действующие в некотором сечении со стороны отброшенной части тела, можно привести к главному вектору и главному моменту. Выделим в рассматриваемом сечении с единичным вектором нормали и около точки М малую площадку D А (рис. 1.7 а).

а б
Рис. 1.7
Главный вектор внутренних сил, действующих на этой площадке, обозначим через D р. Среднее напряжение на площадке D A будет
В пределе при D A® 0 получим напряжение в точке М
Вектор полных напряжений рп зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки D A, характеризуемой вектором В общем случае направление вектора полных напряжений рп не совпадает с направлением вектора нормали Нормальные напряжения возникают, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц по плоскости рассматриваемого сечения. Очевидно, что
Касательное напряжение в свою очередь может быть разложено по направлениям осей ОУ и ОZ (t xy, t.xz). Размерность напряжений – Н/м2. Если вокруг точки А мысленно вырезать параллелепипед, то по его граням будет действовать совокупность напряжений, показанных на рис. 1.8. Нормальные и касательные напряжения в каждом поперечном сечении тела связаны определенным образом с внутренними усилиями, действующими в этом сечении. Если рассмотреть элементарную площадку dА поперечного сечения А бруса с действующими по этой площадке напряжениями s,tу, tz, получим, что на площадку dА действуют элементарные силы s dА, tуdА, tzdA. Тогда можно записать следующие интегральные зависимости: N=
В сопротивлении материалов принято следующее правило знаков для напряжений. Нормальное напряжение s считается положительным, если совпадает по направлению с внешней нормалью п к площадке, и отрицательным, если его направление обратно. Касательные напряжения t считаются положительными, если вектор касательных напряжении следует поворачивать против хода часовой стрелки до совпадения с внешней нормалью, и отрицательными – в противном случае (рис. 1.9). Так как между напряжениями и внутренними усилиями существует интегральная связь, то правило знаков для внутренних силовых факторов обуслов лено принятым правилом знаков для нормальных sи касательных t напряжений. Моменты приняты положительными, как и ранее, если они действуют против хода часовой стрелки.
Рис. 1.8 Рис 1.9
Вопросы для самопроверки 1. Что такое прочность, жесткость, устойчивость конструкции? 2. Что называется брусом, оболочкой, пластинкой? 3. Какая ось называется продольной осью бруса? 4. Что представляет собой расчетная схема конструкции и чем она отличается от собственно конструкции машины или аппарата? 5. Какие основные допущения в отношении свойств материала принимаются сопротивлении материалов? 6. В чем состоит принцип независимости действия сил? 7. В чем заключается гипотеза плоских сечений? 8. По каким признакам и как классифицируются нагрузки? 9. Какая нагрузка называется статической? 10. Что представляет собой интенсивность распределенной нагрузки? 11. В каких единицах измеряются сосредоточенные силы и моменты, интенсивности распределенных нагрузок? 12. Что такое внутренние силы (внутренние силовые факторы)? 13. Какие внутренние усилия (внутренние силовые факторы) могут возникать в поперечных сечениях брусьев, и какие виды деформаций с ними связаны? 14. В чем суть метода сечений? 15. Какие напряжения называются касательным и нормальным? Какова размерность напряжений? Каково правило знаков для напряжений? 16. Какова зависимость между полным, нормальным и касательным напряжениями в точке сечения? 17. Какова связь между напряжениями и внутренними силовыми факторами? 18. Какие деформации называются линейными и какие угловыми?
При растяжении (сжатии)
Для определения опасных напряжений s0 необходимо провести испытания образцов материала на растяжение и сжатие. Растяжение образцов осуществляется на специальных испытательных машинах и сопровождается регистрацией усилий и соответствующих им деформаций. Большинство машин снабжено устройством, записывающим зависимость удлинения образца от приложенной к нему нагрузки. Вычерченная кривая в координатах F–Dl называется машинной диаграммой растяжения образца. Для получения количественных оценок свойств материала диаграмма F – Dl перестраивается в условную диаграмму s – e делением усилия F на первоначальную (до растяжения) площадь поперечного сечения образца A 0и удлинения рабочей части образца Dl на его начальную длину l 0. В результате действия нагрузки длина стержня увеличится на величину Относительной линейной деформацией называется отношение абсолютной продольной деформации к начальной длине стержня:
Рис. 2.3
Кроме продольной деформации стержень испытывает и поперечные деформации, которые определяются по формулам: где
ню нагрузки;
Как показывают эксперименты, при работе стержня в зоне упругости между продольными и поперечными деформациями существует линейная зависимость:
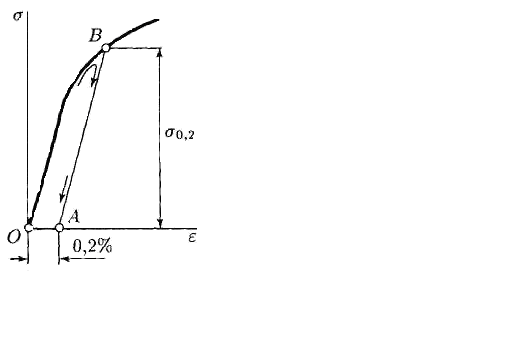
стержня ( стали n = 0,25…0,33; для бронзы – n = 0,32 … 0,35; для алюминия n = 0,35 … 0,36; для пробки – n = 0; для резины – n =0,5). Коэффициент Пуассона всегда положителен, а знак «минус» в формулах (2.5) указывает, что при растяжении стержня его поперечное сечение уменьшается и, наоборот, при сжатии – увеличивается. На рис. 2.4 представлена типичная диаграмма s =f (e) для малоуглеро-дистой стали. Точками отмечены наиболее характерные моменты деформации материала. Наибольшее напряжение, до которого справедлив закон Гука (точка а), называется пределом пропорциональности (sпц). Наибольшее напряжение, до которого материал не получает остаточные деформации (точка b), называется пределом упругости (sу). Предел текучести (s т)– напряжение, при котором происходит рост деформации без заметного увеличения нагрузки (точка с). Для материалов, не имеющих на диаграмме выраженной площадки текучести (участок bс), вводят понятие условного предела текучести s0,2 – напряжения, при котором остаточная деформация равна 0,002, или 0,2 %.Опыты показывают, что разгрузка образца осуществляется всегда по закону Гука, т. е. параллельно участку Оа. При полной разгрузке, когда s = 0, упругие деформации снимаются и остаются только пластические. Следовательно, если на оси деформаций диаграммы s-e отложить от начала координат отрезок ОА, равный 0,002, и провести из точки А линию, параллельную прямой, выражающей закон Гука, то пересечение линии с диаграммой определит точку В, ордината которой будет соответствовать условному пределу текучести s0,2 (рис. 2.5). Временное сопротивление (sв)– условное напряжение, которое соответствует наибольшему усилию в процессе растяжения образца (точка d на рис. 2.4):
Рис. 2.4Рис. 2.5
До точки d деформация равномерно распределяется по длине образца, площадь поперечного сечения образца уменьшается, но не зависит от координаты сечения. Дальнейшее растяжение сопровождается локализацией пластических деформаций, что ведет к образованию шейки (рис. 2.6). Площадь поперечного сечения в зоне локализации пластической деформации резко уменьшается, что ведет к росту истинных напряжений, несмотря на снижение нагрузки (рис. 2.4, участок dк1).
Рис. 2.6
Отношение растягивающего усилия в момент разрушения (Fк) к площади поперечного сечения в месте разрушения (А к) характеризует истинное сопротивление разрушению (SK):
Для цилиндрического образца АK определяется путем замера диаметра в сечении, где произошло разрушение:
Рассмотренные выше напряжения количественно характеризуют прочностные свойства материала. Для характеристики пластических свойств материала определяют относительное удлинение образца после разрыва (d) и относительное сужение после разрыва (y). Первая характеристика определяется отношением:
где lР – длина рабочей части образца после разрушения. Вторая характеристика определяется отношением:
Чем выше значения d и y, тем пластичнее материал. Обычно материал считается пластичным, если d > 5 %. Как правило, yнесколько выше значений d. Противоположным свойству пластичности является хрупкость, т. е. способность материала разрушаться без образования существенных остаточных деформаций. Для хрупких материалов dне превышает 2…5 %. Типичная диаграмма растяжения хрупкого материала показана на рис. 2.7. Она не имеет площадки текучести, и разрушение образца происходит практически без остаточных деформаций. Единственной характеристикой прочностных свойств материала в этом случае является предел прочности sв. Испытания на сжатие пластичных материалов свидетельствуют о том, что пределы пропорциональности, упругости и текучести, как правило, мало отличаются от аналогичных характеристик, полученных при растяжении. Если необходимо отличить предел текучести при растяжении от предела текучести при сжатии, используют дополнительный индекс р для растяжения или с для сжатия. Таким образом, получаем обозначения sтр и sтс. При испытаниях на сжатие пластичного материала невозможно осуществить разрушение образца. Цилиндрический образец получает бочкообразную форму, площадь поперечного сечения образца резко увеличивается (рис. 2.8). Это делает невозможным определение временного сопротивления при сжатии.
F
F Рис. 2.7 Рис. 2.8
При сжатии хрупкого материала вид диаграмм s -e напоминает аналогичную диаграмму при растяжении. Однако, как правило, предел прочности при сжатии значительно выше, чем при растяжении. Характеристики, полученные при растяжении и сжатии, снабжаются дополнительным индексом р – для растяжения или с – для сжатия, например, при растяжении – sвр, при сжатии – sвс. Согласно одной из гипотез механики деформируемого твердого тела, между напряжениями и деформациями существует линейная зависимость (закон Гука, 1676 г.):
где теристика материала. Если заменить в формуле (2.8) выражения s и e, то можно получить другую форму записи закона Гука:
Величина ЕА называется жесткостью стержня при растяжении (сжатии).
Вопросы для самопроверки
1. Что называется стержнем? 2. Какой вид нагружения стержня называются осевым растяжением (сжатием)? 3. Как вычисляется значение продольной силы в произвольном поперечном сечении стержня? 4. Что такое эпюра продольных сил и как она строится? 5. Как распределены нормальные напряжения в поперечных сечениях центрально-растянутого или центрально-сжатого стержня и по какой формуле они определяются? 6. Как связаны гипотеза плоских сечений (гипотеза Бернулли) и закон распределения нормальных напряжений в поперечном сечении растянутого (сжатого) стержня? 7. Что называется удлинением стержня (абсолютной продольной деформацией)? Что такое относительная продольная деформация? Каковы размерности абсолютной и относительной продольных деформаций? 8. Что называется модулем упругости Е? Как влияет величина Е на деформации стержня?
Виды напряженного состояния
В зависимости от количества действующих главных напряжений различают три вида напряженных состояний: линейное, плоское и объемное. Обобщенный закон Гука
Обобщенный закон Гука представляет собой связь между напряжениями и деформациями в случае объемного и как частый случай плоского напряженных состояний. Он может быть получен на основании закона Гука для линейного напряженного состояния и принципа независимости действия сил. Пусть задано произвольное объемное напряженное состояние с главными напряжениями s 1, s 2 и s 3. Представим его в виде суммы трех линейных напряженных состояний. Учитывая, что при линейном напряженном состоянии Деформации в направлении действия главных напряжений равны Эти выражения носят название обобщенного закона Гука, записанного для главных площадок e 1, e 2, e 3 в направлении главных напряжений называются гла
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

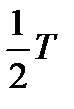 ,
,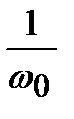 – собственно период низшего тона колебаний конструкции;
– собственно период низшего тона колебаний конструкции; ,
,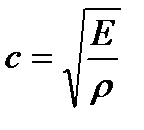 – скорость распространения упругой волны в материале.
– скорость распространения упругой волны в материале.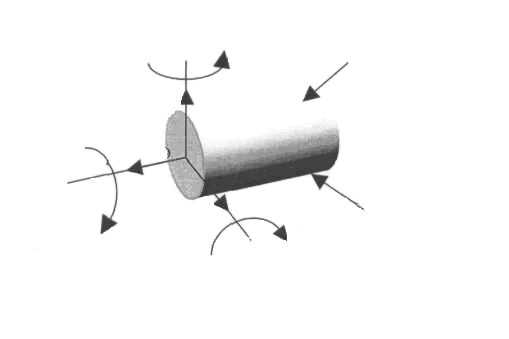

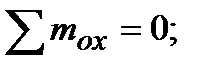





 – нормальная сила равна сумме проекций всех внешних сил, дейст-
– нормальная сила равна сумме проекций всех внешних сил, дейст-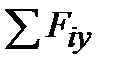 , Qz =
, Qz =  – поперечные силы равны по величине суммам проек-
– поперечные силы равны по величине суммам проек- – крутящий момент равен сумме внешних моментов, действующих
– крутящий момент равен сумме внешних моментов, действующих , Mz =
, Mz = 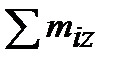 – изгибающие моменты равны суммам внешних момен-
– изгибающие моменты равны суммам внешних момен- .
. .
. . Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора и определяет напряженное состояние в точке М.
. Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора и определяет напряженное состояние в точке М.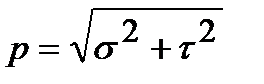 .
. ;
;  ;
; 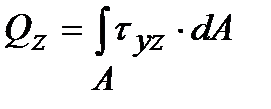
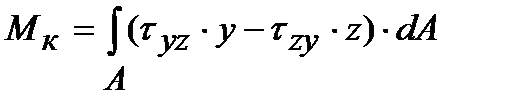 ;
; ;
;  .
.

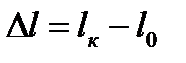 , которая называется абсолютной продольной деформацией, или удлинением стержня (рис. 2.3).
, которая называется абсолютной продольной деформацией, или удлинением стержня (рис. 2.3).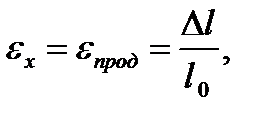 (2.4) где
(2.4) где  – длина стержня до приложения нагрузки;
– длина стержня до приложения нагрузки; – длина стержня после приложения нагрузки.
– длина стержня после приложения нагрузки.
 – абсолютные поперечные деформации;
– абсолютные поперечные деформации;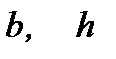 – соответственно ширина и высота сечения до приложения к стерж-
– соответственно ширина и высота сечения до приложения к стерж- – соответственно ширина и высота сечения после приложения нагрузки.
– соответственно ширина и высота сечения после приложения нагрузки. или
или  (2.5) где
(2.5) где  коэффициент Пуассона (безразмерная величина), зависит от материала
коэффициент Пуассона (безразмерная величина), зависит от материала ) и является физической константой материала (для
) и является физической константой материала (для .
.

 .
.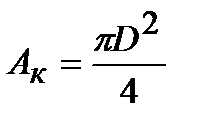 .
. %, (2.6)
%, (2.6) %. (2.7)
%. (2.7)

 , (2.8)
, (2.8) модуль упругости первого рода (модуль Юнга) – механическая харак-
модуль упругости первого рода (модуль Юнга) – механическая харак- ,
, 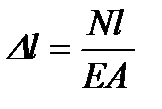 . (2.9)
. (2.9) и
и  запишем выражение для линейной относительной деформации в направлении
запишем выражение для линейной относительной деформации в направлении 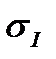 :
: .
. ;
; 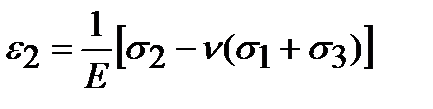 ;
;  .
.


