
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И допущения сопротивления материалов
Сложная форма, присущая реальному телу, и разнообразие физико-ме-ханических свойств материала составляют серьезные препятствия при изучении напряженного состояния тела теоретическим путем. Ввиду этого для каждого частного случая в зависимости от требуемой точности теорию расчета приходится строить на ряде допущений, или гипотез, идеализирующих реальное тело. В сопротивлении материалов принято рассматривать все материалы как однородную сплошную среду, независимо от их микроструктуры. Под однородностью материала понимают независимость его свойств от величины выделенного из тела объема. И хотя в действительности реальный материал, как правило, неоднороден (уже в силу его молекулярного строения), тем не менее указанная особенность не является существенной, поскольку в сопротивлении материалов рассматриваются конструкции, размеры которых существенно превышают не только межатомные расстояния, но и размеры кристаллических зерен. С понятием однородности тесно связано понятие сплошности среды, под которым подразумевают тот факт, что материал конструкции полностью заполняет весь отведенный ему объем, а значит, в теле конструкции нет пустот. Под действием внешних сил реальное тело меняет свои геометрические размеры. После снятия нагрузки геометрические размеры тела полностью или частично восстанавливаются. Свойство тела восстанавливать свои первоначальные размеры после разгрузки называется упругостью. При решении большинства задач в сопротивлении материалов принимается, что материал конструкций абсолютно упругий. Обычно сплошная среда принимается изотропной, т.е. предполагается, что свойства тела, выделенного из нее, не зависят от его ориентации в пределах этой среды. Отдельно взятый кристалл материала анизотропен, но так как в объеме реального тела содержится бесконечно большое количество хаотично расположенных кристаллов, принимается, что материал изотропен. Основные гипотезы, принимаемые при построении теории сопротивления материалов, включают: 1. Гипотезу плоских сечений. Если в теле до деформации мысленно провести плоское сечение, то после деформации это сечение может не остаться плоским. Существует много практически важных случаев, где сечения после деформации остаются плоскими или мало отклоняются от плоскости. В курсе сопротивления материалов, за исключением поперечного изгиба, приходится делать предположение о том, что плоские сечения, проведенные в теле до деформации, остаются плоскими и после деформации (гипотеза Я. Бернулли).
2. Гипотезу о малости перемещений. Перемещения считаем малыми, если тело по отношению к своим общим размерам под нагрузками незначительно изменяет геометрическую форму. Это допущение неприменимо к гибким телам, которые сильно деформируются под нагрузками. 3. Принцип независимости действия сил. Результат воздействия на тело системы сил равен сумме результатов воздействия тех же сил, прилагаемых к телу последовательно и в любом порядке. Под словами «результат воздействия» в зависимости от конкретной задачи следует понимать деформации, внутренние силы, возникающие в теле, и перемещения отдельных точек. Необходимо иметь в виду, что действие отдельных сил системы должно рассматриваться вместе с соответствующими им реакциями связей. Принцип независимости сил, используемый в теоретической механике для абсолютно твердых тел, к деформируемым телам применим только при следующих условиях: – перемещения точек приложения сил малы по сравнению с размерами тела; – перемещения, являющиеся результатом деформации тела, линейно зависят от действующих сил. Такие тела (системы ) называют линейно деформируемыми или подчиняющимися закону Гука. В обычных конструкциях оба эти условия выполняются и поэтому принцип независимости действия сил при расчетах на прочность и жесткость широко применяется. 4. П ринцип Сен-Венана. В точках тела, достаточно удаленных от мест приложения нагрузок, величина внутренних сил весьма мало зависит от конкретного способа приложения этих нагрузок. Этот принцип во многих случаях позволяет производить замену одной системы сил другой системой, статически эквивалентной, что позволяет упростить расчет.
Внешние силы (нагрузки)
Внешними силами называются силы взаимодействия между рассматриваемым элементом конструкции и связанными с ним телами.Внешние силы еще принято называть нагрузками.
Внешние силы (нагрузки), действующие на тело, по способу приложения разделяются на сосредоточенные, распределенные и объемные. Сосредоточенными называются такие нагрузки, которые прикладываются к небольшой площадке тела (размерность Н). Нагрузки, приложенные ко всей или какой-либо части поверхности тела, относятся к распределенным (размерность Н/м2). Эти нагрузки бывают равномерно распределенные, распределенные по треугольнику – треугольные и др. (рис. 1.3).
 
Рис. 1.3 Рис. 1.4
К первым относится, например, давление пара в котле, а ко вторым – давление воды на плотину. Нагрузки, распределенные по всему объему тела, называются объемными (размерность Н/м3). Примером такой нагрузки является собственный вес тела, силы инерции, магнитные силы.Нагрузки, распределенные по линии (рис. 1.4), называются погонными распределенными нагрузками (размерность Н/м). По характеру действия нагрузки разделяются на статические и динамические. Нагрузки, медленно возрастающие по времени от нуля до своего конечного значения, называются статическими (при расчетах силами инерции в этих случаях) здесь пренебрегают. Условие статического нагружения tнараст> где tнараст – время нарастания нагрузки; Т = w0– низшая частота. Динамические нагрузки сопровождаются значительными ускорениями точек деформируемого тела. При этом возникают силы инерции, которыми пренебречь нельзя. Динамические нагрузки делят на мгновенно приложенные, собственно ударные и повторно-переменные. Нагрузка считается мгновенно приложенной, или быстро приложенной, если она возрастает в течение короткого промежутка времени: tнараст< где Силами инерции вдоль оси Х пренебрегают, а в поперечном направлении (вдоль оси У) — их учитывают. При собственно ударном нагружении tнараст< Здесь силы инерции учитываются по всем направлениям координатных линий. В практике динамические нагрузки встречаются либо в чистом виде, либо в комбинации со статическими. Например, действие колеса локомотива на рельс выражается статической нагрузкой от собственного веса, сил инерции и ударной нагрузкой при прохождении рельсовых стыков.
Метод сечений Внутренние силы
Между соседними частицами тела (кристаллами, молекулами, атомами) всегда действуют силы сцепления – внутренние силы. Эти силы стремятся сохранить тело как единое целое. Они препятствуют всякой попытке деформировать тело. Величина этих сил при нагружении тела и в ненагруженном его состоянии будет различной. В сопротивлении материалов не рассматривают начальные внутренние силы в теле (в ненагруженном состоянии), а изучают дополнительные внутренние силы, которые появляются в результате нагружения тела. Внутренние силы часто называются усилиями. Для решения задачи о прочности надо уметь определять внутренние силы. Для этого в сопротивлении материалов широко применяют метод сечений. Сущность метода заключается в следующем. Пусть некоторое тело находится в равновесии под действием системы внешних сил (рис. 1.5 а).
Рассечем (мысленно) тело на две части плоскостью, перпендикулярной продольной оси тела (поперечным сечением). Отбросим правую или левую часть тела. Чтобы оставшаяся часть находилась в равновесии, по плоскости сечения должны действовать внутренние силы. Заменим действие одной части на другую внутренними силами (рис. 1.5 б). Эти внутренние силы по характеру приложения – распределенные, в общем случае они не одинаковы по всему сечению. Внутренние силы могут быть приведены к их равнодействующим: главному вектору R и главному моменту М. Введем ортогональную систему координат с началом в точке О,причем ось Х пусть совпадает с продольной осью тела, а оси Y и Z – с главными центральными осями инерции поперечного сечения (о них будет сказано ниже). Разложим главный вектор R и момент М по осям (рис. 1.6). Получим шесть составляющих, которые называются внутренними силовыми факторами (ВСФ): N –продольная (нормальная) сила, проекция вектора R на ось X; Qz, Qy –поперечные силы, проекции вектора R на оси Z и Y соответственно; Мх = Мк – крутящий момент, составляющая момента М вокруг оси X; Mz, My – изгибающие моменты, составляющие момента М вокруг осей Z и Y соответственно.

а б
Рис. 1.5
Рассмотрим правую часть.
Рис. 1.6
Уравновесим отсеченную часть. Так как отсеченная часть тела находится в равновесии, то для определения шести неизвестных ВСФ. составим шесть уравнений статического равновесия:
из которых поочередно определяются все ВСФ: N = вующих на отсеченную часть, на продольную ось X; Qy = ций всех внешних сил, действующих на отсеченную часть, на оси У и Z соответственно; Mк = на отсеченную часть, относительно оси Х; Mу = тов, действующих на отсеченную часть, относительно осей Y и Z соответственно. Для наглядного представления о характере работы конструкции строят графики изменения ВСФ по длине бруса (вдоль оси Х). Такой график принято называть эпюрой (от французского слова ерuге-чертеж).
Понятие о напряжениях
Внутренние силы, действующие в некотором сечении со стороны отброшенной части тела, можно привести к главному вектору и главному моменту. Выделим в рассматриваемом сечении с единичным вектором нормали и около точки М малую площадку D А (рис. 1.7 а).

а б
Рис. 1.7
Главный вектор внутренних сил, действующих на этой площадке, обозначим через D р. Среднее напряжение на площадке D A будет
В пределе при D A® 0 получим напряжение в точке М
Вектор полных напряжений рп зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки D A, характеризуемой вектором В общем случае направление вектора полных напряжений рп не совпадает с направлением вектора нормали Нормальные напряжения возникают, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц по плоскости рассматриваемого сечения. Очевидно, что
Касательное напряжение в свою очередь может быть разложено по направлениям осей ОУ и ОZ (t xy, t.xz). Размерность напряжений – Н/м2. Если вокруг точки А мысленно вырезать параллелепипед, то по его граням будет действовать совокупность напряжений, показанных на рис. 1.8. Нормальные и касательные напряжения в каждом поперечном сечении тела связаны определенным образом с внутренними усилиями, действующими в этом сечении. Если рассмотреть элементарную площадку dА поперечного сечения А бруса с действующими по этой площадке напряжениями s,tу, tz, получим, что на площадку dА действуют элементарные силы s dА, tуdА, tzdA. Тогда можно записать следующие интегральные зависимости: N=
В сопротивлении материалов принято следующее правило знаков для напряжений. Нормальное напряжение s считается положительным, если совпадает по направлению с внешней нормалью п к площадке, и отрицательным, если его направление обратно. Касательные напряжения t считаются положительными, если вектор касательных напряжении следует поворачивать против хода часовой стрелки до совпадения с внешней нормалью, и отрицательными – в противном случае (рис. 1.9). Так как между напряжениями и внутренними усилиями существует интегральная связь, то правило знаков для внутренних силовых факторов обуслов лено принятым правилом знаков для нормальных sи касательных t напряжений. Моменты приняты положительными, как и ранее, если они действуют против хода часовой стрелки.
Рис. 1.8 Рис 1.9
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.8.110 (0.085 с.) |
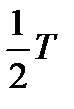 ,
,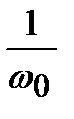 – собственно период низшего тона колебаний конструкции;
– собственно период низшего тона колебаний конструкции; ,
,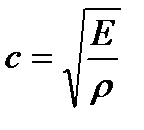 – скорость распространения упругой волны в материале.
– скорость распространения упругой волны в материале.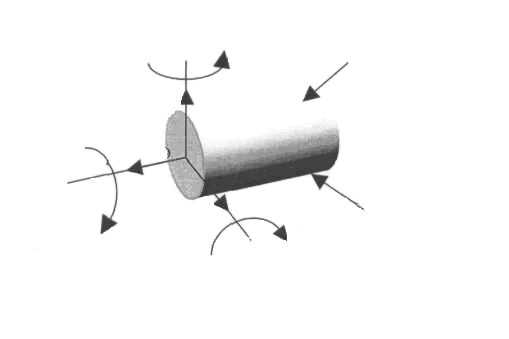

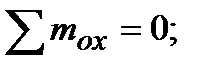





 – нормальная сила равна сумме проекций всех внешних сил, дейст-
– нормальная сила равна сумме проекций всех внешних сил, дейст-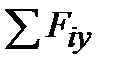 , Qz =
, Qz =  – поперечные силы равны по величине суммам проек-
– поперечные силы равны по величине суммам проек- – крутящий момент равен сумме внешних моментов, действующих
– крутящий момент равен сумме внешних моментов, действующих , Mz =
, Mz = 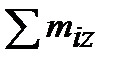 – изгибающие моменты равны суммам внешних момен-
– изгибающие моменты равны суммам внешних момен- .
. .
. . Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора и определяет напряженное состояние в точке М.
. Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора и определяет напряженное состояние в точке М.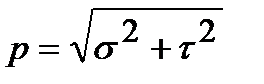 .
. ;
;  ;
; 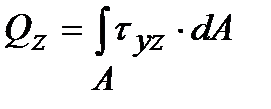
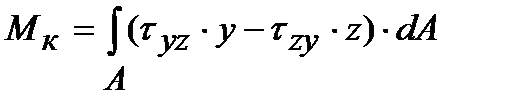 ;
; ;
;  .
.




