
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Объемное напряженное состояние
Объемным, или трехосным называется напряженное состояние, при котором все три главных напряжения отличны от нуля (рис. 3.5). Рассмотрим вопрос определения касательных напряжений в площадках, проходящих через одну из координатных осей x, y или z (рис. 3.1). Используя принцип независимости действия сил и результаты решения прямой задачи для линейного и плоского напряженных состояний, получим:
При a = 450 касательные напряжения достигают наибольших значений:
C учетом того, что s 1 ³ s 2 ³ s 3, получим:
Таким образом, площадка с наибольшим касательным напряжением наклонена под углом α=450 к главным площадкам с напряжениями s 1, s 3. Также можно доказать, что
Обобщенный закон Гука
Обобщенный закон Гука представляет собой связь между напряжениями и деформациями в случае объемного и как частый случай плоского напряженных состояний. Он может быть получен на основании закона Гука для линейного напряженного состояния и принципа независимости действия сил. Пусть задано произвольное объемное напряженное состояние с главными напряжениями s 1, s 2 и s 3. Представим его в виде суммы трех линейных напряженных состояний. Учитывая, что при линейном напряженном состоянии Деформации в направлении действия главных напряжений равны Эти выражения носят название обобщенного закона Гука, записанного для главных площадок e 1, e 2, e 3 в направлении главных напряжений называются главными деформациями. Соотношения обобщенного закона Гука могут быть записаны для любых (не главных) площадок, но так как при этом будут действовать кроме нормальных и касательные напряжения (рис. 3.10), необходимо добавить три соотношения для вычисления угловых деформаций. Таким образом, для произвольных площадок обобщенный закон Гука содержит шесть соотношений, связывающих деформации и напряжения: Как известно, при деформации происходит изменение формы и объема тела. Рассмотрим относительное изменение объема тела при деформировании. Обратимся к рис. 3.1. Объем элементарного прямоугольного параллелепипеда до деформации
Тогда относительное изменение объема может быть вычислено следующим образом: = Раскрывая скобки и пренебрегая слагаемыми более высокого порядка малости по сравнению с e, получим Подставляя e из обобщенного закона Гука, получим
Из формулы видно, что при положительных направлениях главных напряжений относительное изменение объема может быть положительной величиной, если только коэффициент Пуассона будет ν < 0,5. Таким образом, получается, что для всех существующих в природе материалов коэффициент Пуассона изменяется в пределах 0 £ n£ 0,5 и для большинства конструкционных материалов он равен ν = 0,2…0,3. Также можно отметить, что если коэффициент Пуассона равен n = 0,5, то относительное изменение объема равно нулю. Резина имеет n ≈ 0,5, следовательно, при приложении нагрузки её объём практически не меняется, она ведет себя как несжимаемая жидкость. Это свойство резины часто используется в экспериментальной практике. Определим также относительное изменение объема при чистом сдвиге. Так как при чистом сдвиге
Таким образом, относительное изменение объема при чистом сдвиге равно нулю. Рассмотрим изменение удельной потенциальной энергии деформации в теле. Удельной потенциальной энергией деформации u называется величина потенциальной энергии деформации U, накопленной в единице объема тела V. Для линейного напряженного состояния: Используя принцип независимости действия сил, полученный результат можно обобщить на случай объемного напряженного состояния: В случае площадок общего положения (не главных площадок) выражение для удельной потенциальной энергии приобретает вид: Предыдущее выражение можно преобразовать с помощью формул обобщенного закона Гука к виду: Рассмотрим напряженное состояние чистого сдвига. Запишем выражение удельной потенциальной энергии деформации по площадкам чистого сдвига:
С другой стороны, чистый сдвиг – это двухосное напряженное состояние с главными напряжениями
Очевидно, величина удельной потенциальной энергии деформации u не должна зависеть от того, по каким площадкам она записана, поэтому
Таким образом, постоянные упругости материалов, характеризующие жесткость при растяжении и сдвиге и поперечную деформацию, являются зависимыми. Поэтому достаточно определить лабораторным путем при растяжении две характеристики упругости Е и n, а третья G может быть вычислена аналитически.
Теории прочности
Теория прочности дает оценку прочности материала, находящегося в любом напряженном состоянии, по какому-либо решающему фактору (так называемому критерию прочности). За критерий прочности, как показывают многочисленные исследования, можно принимать напряжения, деформации или энергию деформации (полную энергию или энергию изменения формы). Введение критерия прочности позволяет сопоставить данное сложное напряженное состояние с простым, например, с одноосным растяжением и установить при этом такое эквивалентное (расчетное) напряжение s экв ,, которое в обоих случаях дает одинаковый коэффициент запаса прочности. Если в двух напряженных состояниях коэффициенты запаса равны, то они называются равноопасными. Для сравнения различных напряженных состояний за эталон (эквивалент) принято простое растяжение (сжатие) с главным напряжением sэкв. Эквивалентное напряжение sэкв – это такое напряжение, которое следует создать в растянутом образце, чтобы его напряженное состояние было равноопасно заданному напряженному состоянию. Условие прочности записывается в виде sэкв £ [s]. Теории прочности представляют собой гипотезы о критериях, определяющих условия перехода материала в предельное состояние. Рассмотрим некоторые из теорий прочности, заметив предварительно, что общий ход решения задачи построения любой из этих теорий будет следующим. 1. Вводят определенную меру прочности в виде прочности при линейном напряженном состоянии – при осевом растяжении (сжатии) или при чистом сдвиге. 2. Выбирают критерий прочности (напряжение, деформацию или энергию деформации). 3. Устанавливают характеристики прочности для элемента тела в сложном напряженном состоянии и отдельно – для линейного напряженного состояния. 4. Составляя условие равнопрочности сложного и линейного напряженных состояний, получают расчетное уравнение прочности (условие прочности). 5. Проверяют полученное условие прочности на опытном материале. В результате получения нового экспериментального материала приходят к новым критериям прочности или вводят в полученные условия ряд новых постоянных. Заметим, что характер разрушения различных материалов зависит не только от свойств и строения материала, но и от формы образца, способа проведения испытаний, от характера нагружения (статическое, динамическое), от самого напряженного состояния, от начальных напряжений и т.д. Поэтому на первой ступени при разработке той или иной теории прочности приходится выделять лишь основные решающие факторы. Опасное состояние как для пластичных материалов (момент появления больших остаточных деформаций), так и для хрупких (момент появления трещин) лежит на границе применения закона Гука (с известным, достаточным для практики, приближением). Это позволяет при всех дальнейших вычислениях, относящихся к проверкам прочности, пользоваться формулами, полученными при условии применимости закона Гука.
В настоящее время имеется несколько десятков различных теорий прочности, которые последовательно выдвигались в связи с новыми опытными данными, противоречащими некоторым теориям прочности, выдвинутым ранее. Основными теориями прочности принято считать следующие. Первая теория прочности – теория наибольших нормальных напряжений – предложена Ламе (1830 г.) и разработана Рэйкиным (1888 г.). Согласно этой теории, преимущественное влияние на прочность оказывает величина наибольшего нормального напряжения. Предполагается, что нарушение прочности в общем случае сложного напряженного состояния наступит тогда, когда наибольшее нормальное напряжение станет равным опасному (предельному) напряжению при линейном напряженном состоянии (определяется экспериментально на образцах из данного материала). В соответствии с этим при расчетах на прочность ограничивается величина наибольших главных напряжений, которая не должна превышать допускаемого нормального напряжения [s]. Условие прочности имеет вид: sэкв £ [s], где sэкв = s1, если s1³ Итак, первую теорию прочности можно сформулировать следующим образом: прочность материала при сложном напряженном состоянии обеспечена, если наибольшее нормальное напряжение не превышает допускаемого нормального напряжения при линейном напряженном состоянии. Опытная проверка показывает, что эта теория прочности не отражает условий перехода материала в пластическое состояние и дает при некоторых напряженных состояниях удовлетворительные результаты лишь для хрупких материалов (инструментальная сталь, кирпич и т.д.). К недостаткам первой теории прочности следует отнести то, что она учитывает лишь наибольшее главное напряжение, полагая, что два других не влияют на прочность. Вторая теория прочности– теория наибольших деформаций – впервые была высказана французскими учеными Мариоттом и Навье, а затем поддержана Понселе и Сен-Венаном. Согласно этой теории, в качестве критерия прочности принимают наибольшую по абсолютной величине деформацию. Предполагается, что нарушение прочности в общем случае напряженного состояния наступает тогда, когда наибольшая деформация emax достигает своего опасного значения eпред. Последняя определяется при простом растяжении или сжатии образцов из данного материала.
Для пластичного материала условие прочности имеет вид Если, например, Для хрупкого материала условие прочности имеет вид Вторую теорию прочности можно сформулировать так: прочность материала при сложном напряженном состоянии обеспечена, если наибольшая деформация не превышает допускаемой деформации при линейно напряженном состоянии. Опытная проверка второй теории прочности свидетельствует о ее применимости лишь для хрупкого материала (легированный чугун, высокопрочная сталь после низкого отпуска). Третья теория прочности– теория наибольших касательных напряжений. Появление на поверхности образца линий скольжения при возникновении пластических деформаций и разрушении материалов при растяжении по наклонному сечению, где действуют наибольшие касательные напряжения, дает основание принять эти напряжения в качестве критерия прочности. Впервые такое предположение было высказано французским физиком Кулоном в 1773 г. и подтверждено опытами Треска, Геста и других ученых. Третья теория прочности предполагает, что предельное состояние в общем случае наступает тогда, когда наибольшее касательное напряжение tmaxдостигает опасного значения tmin, котороеопределяется при достижении предельного состояния в случае простого растяжения. Условие прочности имеет вид: Откуда Таким образом, третья теория прочности может быть сформулирована следующим образом: прочность материала при сложном напряженном состоянии обеспечена, если наибольшее касательное напряжение не превышает допускаемого касательного напряжения для линейного напряженного состояния. Третья теория прочности достаточно хорошо подтверждается опытами для пластичных материалов, одинаково работающих на растяжение и сжатие. Недостаток ее заключается в том, что она не учитывает среднего по величине главного напряжения s2, которое, как показывают эксперименты, также оказывает некоторое, хотя во многих случаях и незначительное, влияние на прочность материала. Четвертая теория прочности – теория наибольшей удельной потенциальной энергии формоизменения. Рядом авторов было высказано предположение, что опасное состояние материала зависит не только от величины деформаций или напряжений в отдельности, а от их совокупности, т.е. от величины потенциальной энергии деформаций (которая выражается через все три главных напряжения). В конце XIX в. итальянский ученый Бельтрами предложил в качестве критерия прочности принимать количество полной потенциальной энергии деформации в единице объема. Однако это предложение не нашло экспериментального подтверждения. В 1904 г. Губер, в 1913 г. Мезес и в 1924 г. Генки предложили в качестве критерия прочности принять не всю потенциальную энергию деформации, а только ту ее часть, которая идет на изменение формы тела.
В связи с этим в качестве критерия прочности принимается величина уде-льной потенциальной энергии формообразования, т.е. потенциальной энергии, идущей только на изменение формы тела, не учитывающей деформации тела без искажения его формы. В соответствии с этой теорией прочности нарушение прочности детали обусловлено переходом материала детали в пластическое состояние и появлением недопустимых пластических деформаций. Опасное состояние (текучесть) наступает тогда, когда удельная потенциальная энергия формоизменения достигает своего предельного значения. Формулу удельной потенциальной энергии изменения формы получим из формулы полной удельной потенциальной энергии деформации (3.5), подставляя значение коэффициента Пуассона, равного ν = 0,5. Получим
Условие прочности имеет вид
Откуда Итак, согласно четвертой теории прочности, прочность материала при сложном напряженном состоянии обеспечена, если наибольшая удельная потенциальная энергия формоизменения не превышает допускаемой удельной потенциальной энергии формоизменения для линейного напряженного состояния. Опыты хорошо подтверждают третью и четвертую теорию прочности для пластичных материалов, одинаково работающих на растяжение и сжатие. Появление в материале малых пластических деформаций четвертой теорией определяется более точно, чем третьей. Теория прочности Мора. Известно, что один и тот же материал в различных условиях нагружения ведет себя неодинаково, и деление материалов на хрупкие и пластичные имеет смысл только применительно к стандартным методам испытания образцов. В настоящее время утвердилась точка зрения, согласно которой каждый материал может разрушаться и хрупко, и пластично в зависимости от своей структуры, характера напряженного состояния, соотношения главных напряжений, скорости нагружения, температуры и т.д. Следовательно, идеальной выглядела бы такая теория, которая охватывала бы оба состояния – хрупкое и пластичное), конкретизируя при этом предельную стадию – разрушение или наступление текучести. Желательно также, чтобы учитывалось различие механических характеристик при растяжении и сжатии, если такое наблюдается в эксперименте. Теория Мора, отличающаяся от всех приведенных ранее, основана на предположении, что прочность материала в общем случае напряженного состояния зависит главным образом от величины наибольшего s 1и наименьшего s 3главных напряжений, а среднее s 2 на прочность влияет незначительно. Эта теория целиком базируется на опытных данных и не нуждается в дополнительной экспериментальной проверке. Эквивалентное напряжение по этой теории определяется по формуле s экв = s 1 – ks 3, где Для хрупких материалов отношение Наилучшие результаты эта теория дает для случая, когда s1 > 0, а s3 < 0. Это обстоятельство существенно, так как при решении практических задач напряженное состояние такого рода встречается чаще других. Для многих пластичных материалов, у которых sтр = sтс, теория прочности Мора совпадает с теорией максимальных касательных напряжений.
Вопросы для самопроверки
1. Какое напряженное состояние называется пространственным (трехосным), плоским (двухосным) и линейным (одноосным)? 2. Каково правило законов для нормальных и касательных напряжений? 3. Сформулируйте закон парности касательных напряжений. 4. Чему равна сумма нормальных напряжений, действующих на любых двух взаимно перпендикулярных площадках? 5. Что такое главные напряжения и главные площадки? Как расположены главные площадки относительно друг друга? 6. Чему равны касательные напряжения на главных площадках? 7. Напишите формулы для определения главных напряжений и углов наклона главных площадок. 8. Как определить положение главной площадки, по которой действует главное напряжение smax в общем случае плоского напряженного состояния? 9. Чему равны максимальные значения касательных напряжений в случае плоского напряженного состояния? 10. Какие площадки называются площадками сдвига и под каким углом они наклонены к главным площадкам? 11. Чему равна сумма нормальных напряжений на любых трех взаимно перпендикулярных площадках? 12. Чему равны максимальные и минимальные касательные напряжения (при заданных напряжениях s1, s2, s3) и по каким площадкам они действуют? 13. Напишите формулы обобщенного закона Гука? 14. На основе какого из допущений, принятых в курсе сопротивления материалов, получен обобщенный закон Гука? 15. Что называется полной удельной потенциальной энергией деформации, удельной потенциальной энергией изменения объема и формы? 16. Какой случай плоского напряженного состояния называется чистым сдвигом? 17. Напишите закон Гука при сдвиге. 18. Докажите, что объемная деформация при чистом сдвиге равна нулю. 19. Напишите зависимость между модулем упругости Е и модулем сдвига G. 20. Что называется предельным опасным состоянием материала? Чем характеризуется наступление опасного состояния для пластичных и хрупких материалов? 21. Какая точка тела называется опасной? 22. Что называется допускаемым напряженным состоянием? 23. Почему определение прочности в случаях сложного (плоского или пространственного) напряженного состояния приходится производить на основе результатов опытов, проводимых при одноосном напряженном состоянии? 24. Что представляют собой теории прочности? 25. Сформулируйте первую и вторую теории прочности. Укажите область применения.
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 594; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.190.167 (0.053 с.) |
 ;
;  ;
; 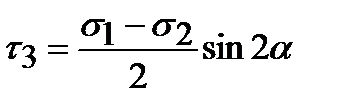 .
. ;
;  ;
; 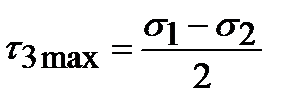 .
. .
. ..
.. и
и  запишем выражение для линейной относительной деформации в направлении
запишем выражение для линейной относительной деформации в направлении 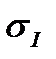 :
: .
. ;
; 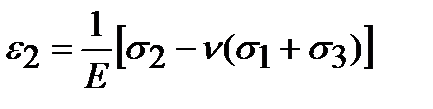 ;
;  .
. ;
;  ;
;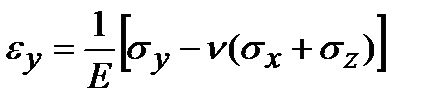 ;
;  ;
; 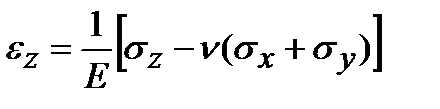 ;
;  .
. . При деформировании длина каждого ребра может измениться на некоторую величину D и объем того же параллелепипеда после деформирования будет
. При деформировании длина каждого ребра может измениться на некоторую величину D и объем того же параллелепипеда после деформирования будет 
 .
. .
. .
.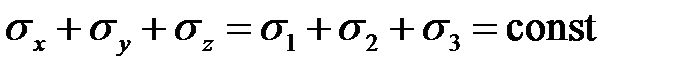 Учитывая, что, запишем выражение для q в виде
Учитывая, что, запишем выражение для q в виде .
. ,
,  ,
, 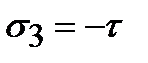 , то
, то .
. .
.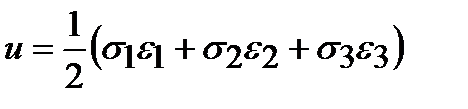 .
. .
. . (3.5)
. (3.5)
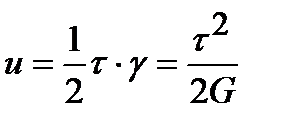 .
. ;
;  , поэтому можно записать u как
, поэтому можно записать u как .
. , откуда, как упоминалось ранее
, откуда, как упоминалось ранее  .
.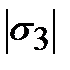 ;
;  , если
, если  .
. , где
, где  .
.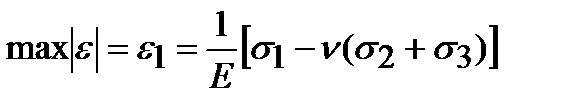 , то
, то  .
. ,
,  .
. , где
, где 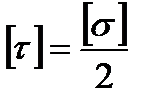 .
. .
.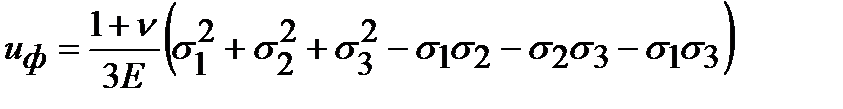 ,
, , где
, где  .
. .
.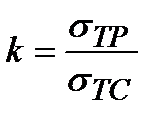 – для пластичных материалов.
– для пластичных материалов. заменяется на
заменяется на  . Условие прочности запишется в виде: s 1 – ks 3 £ [s]p.
. Условие прочности запишется в виде: s 1 – ks 3 £ [s]p.


