
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 4. Геометрические характеристикиСодержание книги
Поиск на нашем сайте
Плоских сечений
Вопросы лекции: 1. Статические моменты сечений. 2. Моменты инерции сечений. 3. Главные оси инерции и главные моменты инерции. 4. Моменты инерции простых сечений.
Рис. 4.1 сит от выбора системы координат. При расчетах на изгиб, кручение, сложное сопротивление и устойчивость используются более сложные геометрические характеристики: статические моменты, моменты инерции сечений, которые зависят не только от формы и размеров сечений, но также от положения осей и точек (полюсов), относительно которых они вычисляются.
Статические моменты сечений
Статическим моментом S z сечения относительно оси z называется геометрическая характеристика, определяемая интегралом вида где у – расстояние от элементарной площадки dA до оси z. Если отождествить площадь с силой, действующей перпендикулярно плоскости чертежа, то интеграл (4.1) можно рассматривать как сумму моментов сил относительно оси z. По известной из теоретической механики теореме Вариньона о моменте равнодействующей можно написать где A – площадь сечения (представляет собой равнодействующую); ус – координата (плечо равнодействующей); с – центр тяжести сечения. Аналогично статический момент относительно оси у равен откуда следуют формулы для определения координат центра тяжести Статические моменты могут быть положительными, отрицательными и равными нулю. В частности, относительно любых центральных осей, проходящих через центр тяжести С (оси обозначаются хс, ус), статические моменты Для вычисления статического момента сложной фигуры ее разбивают на части, для каждой из которых известна площадь и положение центра тяжести (zс, у с):
Таким образом, статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей сечения относительно той же оси.
Моменты инерции сечений
К геометрическим характеристикам плоских сечений относятся также моменты инерции. Различают осевые, полярные и центробежные моменты сечений. Осевым моментом инерции сечения называется взятая по всему сечению сумма произведений элементарных площадок на квадраты их расстояний до некоторой оси, лежащей в плоскости рассматриваемого сечения. Так, относительно осей у и z (рис. 4.1) осевые моменты инерции определяются интегралами вида: Величина осевого момента инерции служит характеристикой способности балки сопротивляться деформации изгиба. Полярным моментом инерции сечения называется взятая по всему сечению сумма произведений элементарных площадок на квадраты их расстояний до некоторой точки О сечения (рис. 4.1):
где r – расстояние от площадки dА до полюса. Полярный момент инерции характеризует способность сечения сопротивляться деформации кручения. Центробежным моментом инерции сечения относительно осей Оу и Оz называется взятая по всему сечению сумма произведений элементарных площадок на расстояния их до этих осей. Центробежный момент инерции сечения определяются интегралом
Если полярный момент инерции вычисляется относительно начала системы координат (рис. 4.1), то
следовательно, т.е. сумма осевых моментов инерции сечения относительно любых двух взаимно перпендикулярных осей, проходящих через данную точку, равна полярному моменту инерции этого сечения относительно этой точки.
Центробежный момент инерции сечения относительно осей, хотя бы одна из которых является осью симметрии, равен нулю. Действительно для симметричной фигуры всегда можно выделить два элемента ее площади (рис. 4.2), которые имеют одинаковые ординаты у1=у2=у, и равные по величине, но противоположные по знаку абсциссы z1=z и z2=–z. Тогда
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.162.21 (0.005 с.) |

 Как было показано выше, при растяжении и сжатии площадь поперечного сечения полностью характеризует прочность и жесткость стержня. Возьмем некоторое поперечное сечение бруса (рис. 4.1). Если представить себе сечение состоящим из бесчисленного множества площадок dA, то площадь всего сечения
Как было показано выше, при растяжении и сжатии площадь поперечного сечения полностью характеризует прочность и жесткость стержня. Возьмем некоторое поперечное сечение бруса (рис. 4.1). Если представить себе сечение состоящим из бесчисленного множества площадок dA, то площадь всего сечения  . Площадь является простейшей геометрической характеристикой сечения (размерность м2). Отметим два важных свойства: площадь всегда положительна и не зави-
. Площадь является простейшей геометрической характеристикой сечения (размерность м2). Отметим два важных свойства: площадь всегда положительна и не зави- , (4.1)
, (4.1) , (4.2)
, (4.2) , (4.3)
, (4.3) ;
;  . (4.4)
. (4.4) . Размерность статических моментов м3.
. Размерность статических моментов м3. ;
; . (4.5)
. (4.5)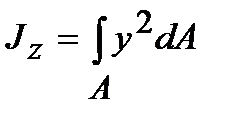 ;
;  . (4.6)
. (4.6) , (4.7)
, (4.7) . (4.8)
. (4.8) и
и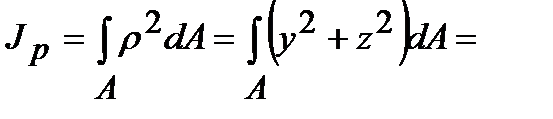
 +
+  ,
, , (4.9)
, (4.9) .
.


