
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие об устойчивости. Задача Эйлера
Из теоретической механики известно, что равновесие абсолютно твердого тела может быть устойчивым (рис. 9.1а) безразличным (рис. 9.1б) и неустойчивым (рис 9.1в и г).
а б в г Рис. 9.1
Равновесное состояние деформируемой системы, например стержня, также может быть устойчивым (рис. 9.2а), безразличным (критическим) (рис. 9.2б) и неустойчивым (рис. 9.2в).
а б в
Рис. 9.2
Строгое определение устойчивости по теореме Пуанкаре звучит так.
Равновесие стержня устойчиво, если, задавшись любой вели-чиной прогиба f > 0, всегда можно указать такую конечную величину возмущения Нагрузка, при которой начальная (исходная) форма равновесия стержня перестает быть устойчивой, называется критической и обозначается Fкр. Приложение к стержню силы Рис. 9.3 вызывает его продольный изгиб. Явление перехода системы от одного равновесного состояния к другому равновесному состоянию, называется потерей устойчивости системы. В некоторых случаях при потере устойчивости система, переходя в новое устойчивое равновесное состояние, продолжает выполнять свои функции. Однако в подавляющем большинстве случаев потеря устойчивости системы сопровождается возникновением больших перемещений, пластических деформаций или ее полным разрушением. Поэтому сохранение исходного (расчетного) равновесного состояния системы является важной задачей и одной из основных проблем сопротивления материалов. Но потеря устойчивости упругого равновесия возможна и при других видах деформаций. Так, при прямом изгибе балок направление прогиба балки может существенно отклониться от линии действия нагрузки (рис. 9.4 б), и, наконец, при действии внутреннего давления на цилиндрическую оболочку ее деформации в некоторый момент перестают быть осесимметричными, оболочка искривляется и принимает некоторую новую форму (рис. 9.4 в).
а б в
Разрушение от сжимающих критических нагрузок наступает внезапно при отсутствии внешних признаков приближающей потери устойчивости. Практически мгновенно происходит изменение характера нагружения, приводящего к разрушению конструкции. Так, например, продольно сжатый прямолинейный стержень принимает изгибную форму равновесия. Поэтому явление потери устойчивости сжимаемого бруса называют также продольным изгибом бруса. Впервые поставил и решил задачу о потере устойчивости прямолинейной формы сжатого стержня академик Петербургской академии наук Леонард Эйлер (1707 – 1783) в 1744 г. Рассмотрим решение задачи об устойчивости сжатого стержня. Пусть стержень, оба конца которого закреплены шарнирно, сжат силой F кр(рис. 9.5). Стержень искривился так, что в сечении x прогиб составил z.
Приближенное дифференциальное уравнение изогнутой оси балки имеет вид: Рис. 9.5
Изгибающий момент в сечении x в изогнутом состоянии равен моменту силы Fкр, но обратного направления, а следовательно, и знака Тогда дифференциальное уравнение изогнутой оси балки в направлении минимальной жесткости будет Обозначая Его общее решение имеет вид: На опорах стержня прогиб равен нулю, т.е. 1) при x = 0, z = 0; 2) при x = l, z = 0. Подставляя первое условие в уравнение прогибов, получим С = 0, из второго условия получим Последнее соотношение справедливо при Минимальное действительное значение критической силы получится при n= 1: Это и есть формула Эйлера для критической силы. Прогиб стержня с шарнирным закреплением концов происходит по синусоиде с одной полуволной
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 255; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.244.83 (0.008 с.) |







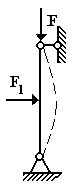 Пусть идеально прямой стержень нагружен строго центральной продольной силой
Пусть идеально прямой стержень нагружен строго центральной продольной силой  (рис. 9.3). При таких предположениях прямолинейная форма стержня всегда будет являться возможной формой равновесия. Об устойчивости этой формы равновесия стержня можно судить по реакции ее на поперечную нагрузку F1. При отсутствии силы F малая сила F1 вызывает малый прогиб стержня. При небольшой силе F положение стержня не изменится, а равновесие его сохранится устойчивым.
(рис. 9.3). При таких предположениях прямолинейная форма стержня всегда будет являться возможной формой равновесия. Об устойчивости этой формы равновесия стержня можно судить по реакции ее на поперечную нагрузку F1. При отсутствии силы F малая сила F1 вызывает малый прогиб стержня. При небольшой силе F положение стержня не изменится, а равновесие его сохранится устойчивым.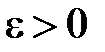 , что при
, что при  величина прогиба
величина прогиба  ни в одной точке системы не достигнет величины f, т.е. будет n < f.
ни в одной точке системы не достигнет величины f, т.е. будет n < f.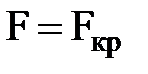 или
или 
 .
. .
. . (9.1)
. (9.1) , из (9.1) получим линейное дифференциальное уравнение второго порядка относительно прогиба z
, из (9.1) получим линейное дифференциальное уравнение второго порядка относительно прогиба z  .
. , где С и D – постоянные интегрирования, определяемые из условий на опорах.
, где С и D – постоянные интегрирования, определяемые из условий на опорах. .
. , где n – любое целое число. Тогда имеем
, где n – любое целое число. Тогда имеем 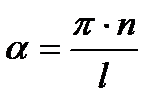 и с учетом принятого ранее обозначения, получим
и с учетом принятого ранее обозначения, получим .
. . (9.2)
. (9.2) .
.


