
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пружинный, физический и математический маятники.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Материальную точку, совершающую колебания, называют осциллятором (от английского слова oscillation — колебание). Таким образом, рассмотренные выше колебания представляют собой частные случаи свободных колебаний гармонического осциллятора:
решение, которого будем записывать в виде: x (t)= Acos (ω0 t +a), где A – амплитуда колебаний; ω0 – собственная частота; величина ω0 t +a–фаза колебания. Примерами гармонического осциллятора являются пружинный, физический и математический маятники. 1. Пружинный маятник.
Пружинным маятником называется система, состоящая из груза массы m, подвешенного на пружине и совершающий гармонические колебания под действием упругой силы (рис.15.1). Обозначим смещение пружины из положения равновесия x. Тогда сила, возникающая в пружине при выведении шарика из положения равновесия, будет равна F = -kx. Эта сила пропорциональна величине смещения и направлена к положению равновесия. В таком случае уравнение движения шарика, согласно второму закону Ньютона, запишется в виде
или
Обозначив
Из уравнения (15.3.2) следует, что движение пружинного маятника описывается линейным однородным дифференциальным уравнением второго порядка. Решение уравнения (15.3.2) имеет вид x(t) = A cos (wt+j), где Тогда 2. Физический маятник
Твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции называется физическим маятником (рис.15.2). Покажем, что и физический маятник будет совершать гармонические колебания. В положении равновесия центр инерции маятника (С) находится под точкой подвеса (О) на одной с ней вертикали. При отклонении маятника от положения равновесия на угол j возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен произведению силы тяжести на плечо силы (d): M = mgd или
где Согласно основному уравнению динамики вращательного движения, вращательный момент равен M = Ie (15.3.3.) или
В случае малых колебаний sinj~j и, приравнивая (15.3.3) и (15.3.4), получим уравнение колебаний физического маятника:
или
Введем обозначение
и перепишем уравнение (15.3.5) в виде
Уравнение колебаний физического маятника (15.3.6) представляет собой однородное линейное дифференциальное уравнение второго порядка. Из теории дифференциальных уравнений известно, что решением уравнения (15.3.6) будет функция вида j(t) = j0 cos (wt+a), т.е. при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота и период которых определяются из следующих соотношений:
где Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.
3. Математический маятник
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешено тело точечной массы m и совершающей колебания под действием силы тяжести. Приближенно можно считать математическим маятником небольшой, нетяжелый шарик, подвешенный на тонкой длинной нити (рис.15.3). Отклоним маятник от положения равновесия на угол a и предоставим ему возможность совершать колебания. На маятник в отклоненном состоянии действует возвращающая сила Fв = -mg sina. Она направлена по касательной к траектории движения шарика в сторону положения равновесия. Согласно второму закону Ньютона, уравнение движения математического маятника запишется в виде
В общем случае решение уравнения сложно. Рассмотрим случай, когда отклонение маятника от положения равновесия настолько малы, что синус угла можно считать пропорциональным величине угла: sina ~ a. Тогда смещение по дуге приближенно можно считать равным смещению вдоль горизонтальной хорды и синус угла a заменить отношением смещения x к длине нити
Тогда
Введем обозначение
и подставляя его в уравнение (15.3.7), получим уравнение движения математического маятника:
Из вида уравнения (15.3.8) следует, что движение математического маятника описывается линейным однородным дифференциальным уравнением второго порядка. Из теории дифференциальных уравнений известно, что решением уравнения (15.3.8) является функция вида x(t) = A sin (wt+y) или x(t) = A cos (wt+a), т.е. математический маятник совершает гармонические колебания с частотой
и периодом
Таким образом, период колебаний математического маятника зависит только от ускорения силы тяжести в данном месте Земли и от длины маятника. Математический маятник представляет собой частный случай физического маятника, где вся масса твердого тела сосредоточена в одной точке, находящейся на постоянном расстоянии от точки вращения.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 6579; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.248.88 (0.007 с.) |

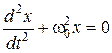 , (15.3.1)
, (15.3.1)

 .
. , перепишем уравнение движения пружинного маятника:
, перепишем уравнение движения пружинного маятника: . (15.3.2)
. (15.3.2)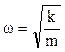 - частота гармонических колебаний.
- частота гармонических колебаний. - период колебаний пружинного маятника.
- период колебаний пружинного маятника.
 ,
, - расстояние между центром инерции и точкой подвеса.
- расстояние между центром инерции и точкой подвеса.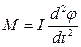 . (15.3.4)
. (15.3.4)
 . (15.3.5)
. (15.3.5)
 . (15.3.6)
. (15.3.6) ;
; .
.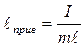 - приведенная длина физического маятника (на рис. 15.2 приведенная длина соответствует отрезку ОО/). Точка О/ на продолжении прямой ОС, отстоящей от точки О подвеса маятника на расстоянии приведенной длины, называется центром качаний физического маятника.
- приведенная длина физического маятника (на рис. 15.2 приведенная длина соответствует отрезку ОО/). Точка О/ на продолжении прямой ОС, отстоящей от точки О подвеса маятника на расстоянии приведенной длины, называется центром качаний физического маятника.
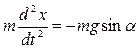 .
.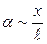
 (15.3.7)
(15.3.7)
 (15.3.8)
(15.3.8)
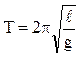 .
.


