
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соотношение неопределенности Гейзенберга для: координат и импульса, энергии и времени. Невозможность одновременного измерения двух величин в квантовой физике.
Волновые свойства микрочастиц вносят ограничения в возможность применять к таким частицам понятия координаты и импульса в их классическом смысле. Например, электрон (и любая другая микрочастица) не может иметь одновременно точных значений координаты x и компоненты импульса рх. Неопределенности значений x и рх удовлетворяют соотношению:
неопределенность импульса вдоль осей у и z соответственно равны:
Данные соотношения называются соотношения неопределенностей Гейзенберга. В этих уравнениях Δх, Δy, Δz означают интервалы координат, в которых может быть локализована частица, описываемая волной де Бройля, если проекция ее импульса по осям координат заключены в интервалах Δрх, Δрy, Δрz соответственно. Определим значение координаты х свободно летящей микрочастицы, поставив на ее пути щель ширины Δх, расположенную перпендикулярно к направлению движения частицы (рис.22.1). Так как частица обладает волновыми свойствами света, то при прохождении через щель, размер которой сравним с длиной волны де Бройля частицы, наблюдается дифракция. Дифракционная картина, наблюдаемая на экране, характеризуется главным максимумом, расположенным симметрично оси у и побочными максимумами по обе стороны от главного (мы их рассматривать не будем, т.к. основная доля интенсивности приходится на главный максимум). До прохождения частицы через щель частица двигалась вдоль оси у, поэтому составляющая импульса рх =0 и Δрх = 0, а координата х частицы является совершенно неопределенной. В момент прохождения частицы через щель положение в направлении оси Х определяется с точностью до ширины щели, т.е. с точностью до Δх. В этот же момент вследствие дифракции частица отклонится от первоначального угла φ, соответствующий первому дифракционному максимуму, и будет двигаться в пределах угла 2φ. Следовательно, появится неопределенность в значении составляющей импульса частицы вдоль оси Х, которая как видно из рисунка равна:
Из теории дифракции известно, что первый минимум соответствует углу φ, соответствующей условию
где Δх – ширина щели, λ – длина волны де Бройля. Следовательно, получим
- соотношение неопределенности Гейзенберга. В этом уравнение было учтено, что у некоторых частиц, попадающих за пределы главного максимума, величина
Соотношение неопределенностей энергии Е и времени t:
где ΔЕ – неопределенность энергии частицы, которая находится в течение времени Δt в состоянии с энергией Е. Энергия частицы в данном состоянии может быть определена тем точнее, чем дольше частица находится в этом состоянии.
Задание состояния квантовой частицы. Волновая функция, ее статистический смысл. Условие нормировки. Уравнение Шредингера. Положение частицы в пространстве в данный момент времени определяется в квантовой механике заданием волновой функции (пси-функции) Ψ (х, у, z, t). Вероятность d w того, что частица находится в момент времени t в малом объеме d V вблизи точки М (х, у, z), равна:
где
Интенсивность волны де Бройля определяется величиной Из определения Ψ-функции следует условие нормировки вероятностей:
где тройной интеграл по объему вычисляется по координатам х, у и z от - Волновая функция Ψ(х,у,z,t) является основной характеристикой состояния микрообъектов (атомов, молекул, элементарных частиц). С ее помощью вычисляется среднее значение физической величины L, характеризующей объект, находящийся в состоянии, описываемом волновой функцией Ψ
где <L> — среднее значение величины L. Временным уравнением Шредингера называется основное дифференциальное уравнение квантовой механики относительно волновой функции Ψ (х, у, z, t) (оно не выводится, а является фундаментальным и основано на тех экспериментальных результатах, которые были накоплены при изучении микрообъектов). Временное уравнение определяет Ψ-функцию для микрочастиц, движущихся в силовом поле с потенциальной энергией U(x, у, z, t) со скоростью υ<<с, где с — скорость света в вакууме. Уравнение Шредингера имеет вид
где Δ — оператор Лапласа h — постоянная Планка, Уравнение Шредингера дополняется условиями, которые накладываются на Ψ-функцию: а) функция Ψ должна быть конечной, однозначной и непрерывной; б) производные в) функция В случае, когда функция потенциальной энергии U не зависит от времени (
причем координатная часть волновой функции Ψ(х, у, z) удовлетворяет стационарному уравнению Шредингера:
где W — энергия частицы.. Функции Ψ, удовлетворяющие уравнению Шредингера при заданном виде U =U{x, у, z), называются собственными функциями. Они существуют лишь при определенных значениях энергии W, называемых собственными значениями энергии. Совокупность собственных значений W образует энергетический спектр частицы. В зависимости от вида функции U {х, у, z) энергетический спектр частицы может быть дискретным или непрерывным. Отыскание собственных значений и собственных функций составляет важнейшую задачу квантовой механики. Если частица находится в определенном энергетическом состоянии с энергией W = const, то вероятность dw обнаружить ее в элементе объема dV не зависит от времени:
Такое состояние частицы называется стационарным состоянием. Атом, находящийся в стационарном состоянии, имеет постоянную энергию и не излучает электромагнитные волны.
Общее уравнение Шредингера Рассмотрим свободно движущуюся частицу. Согласно теории де Бройля ей можно сопоставить плоскую волну, описываемую уравнением
Учитывая, что длина волны де Бройля
Продифференцировав выражение (22.5.2) один раз по t, а второй раз дважды по х, получим
Отсюда
В нерелятивистской классической механике кинетическая энергия W и импульс р свободной частицы связаны соотношением
Подставив в это соотношение выражения для W и р2 получим уравнение
которое совпадает с временным уравнением, если предположить, что потенциальная энергия U = 0. В случае частицы, движущейся в силовом поле, характеризуемом потенциальной энергией U, кинетическая энергия W и импульс р связаны соотношением
получим
Умножив соотношение (22.5.4.) на Ψ придем к уравнению
соответствующего общему уравнению Шредингера.
Основными задачами квантовой механики являются: 1. Поведение свободной частицы 2. Поведение частицы в потенциальной яме или с бесконечно высокими стенками 3. Прохождение частицы через потенциальный барьер (туннельный эффект) 4. Квантовый гармонический осциллятор. Более подробно рассмотрим задачу о движении свободной частицы.
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 601; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.202.4 (0.014 с.) |








 . Невозможность одновременно точно определить координату и соответствующую проекцию импульса, не связана с несовершенством методов измерения или измерительных приборов, а является следствием двойственной корпускулярно-волновой природы микрообъектов. Соотношение неопределенностей было получено с использованием одновременно классических характеристик движения частицы (импульс, координата) и наличия у нее волновых свойств. Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей Гейзенберга является квантовым ограничением применимости классической механики к микрообъектам.
. Невозможность одновременно точно определить координату и соответствующую проекцию импульса, не связана с несовершенством методов измерения или измерительных приборов, а является следствием двойственной корпускулярно-волновой природы микрообъектов. Соотношение неопределенностей было получено с использованием одновременно классических характеристик движения частицы (импульс, координата) и наличия у нее волновых свойств. Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей Гейзенберга является квантовым ограничением применимости классической механики к микрообъектам. .
.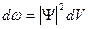
 — квадрат модуля Ψ-функции:
— квадрат модуля Ψ-функции:  . Здесь
. Здесь  —функция, комплексно сопряженная с Ψ. Величина
—функция, комплексно сопряженная с Ψ. Величина  (22.4.1)
(22.4.1)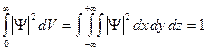 (22.4.2)
(22.4.2) до +
до + 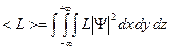 (22.4.3)
(22.4.3) , (22.4.4)
, (22.4.4) , т — масса частицы,
, т — масса частицы, 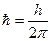
 - мнимая единица.
- мнимая единица. должны быть непрерывны;
должны быть непрерывны; должен быть конечным.
должен быть конечным. ) решение временного уравнения Шредингера имеет вид:
) решение временного уравнения Шредингера имеет вид:
 (22.4.5)
(22.4.5)
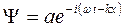 (22.5.1.)
(22.5.1.) и энергия
и энергия  и
и 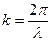 - волновое число придем к выражению
- волновое число придем к выражению (22.5.2)
(22.5.2)


 , (22.5.3.)
, (22.5.3.)
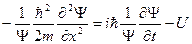 (22.5.4.)
(22.5.4.) ,
,


