
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерференция волн. Стоячие волныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Интерференцией волн называется явление наложения волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других в зависимости от соотношения между фазами этих волн. Интерферировать могут только когерентные волны, которым соответствуют колебания, совершающиеся вдоль одного и того же или близких направлений.
Две волновых процесса называются когерентными, если они согласованно протекают в пространстве и времени. Две монохроматические волны называются когерентными, если равны их частоты, т.е. разность их фаз не зависит от времени. Синусоидальные волны, частоты которых одинаковы, когерентны всегда. Рассмотрим два точечных источника S1 и S2, которые испускают сферические волны с одинаковой амплитудой А0 и с постоянной разностью фаз (рис. 17.3.):
где r1 и r2 - расстояния от источников волн до рассматриваемой точки М; k – волновое число; φ01 и φ02 – начальные фазы двух сферических волн соответственно. По принципу суперпозиции, результирующее колебание в точке М описывается формулой
где А – амплитуда результирующего колебания, φ – фаза результирующего колебания. Для нахождения А и φ воспользуемся методом векторных диаграмм (рис.16.4).
Из рисунка амплитуда результирующей волны
где амплитуды волн Так как для двух когерентных источников φ1 –φ2=const, то результат интерференции двух волн зависит от величины (r 2 -r 1), называемой геометрической разностью хода. интерференционный максимум
наблюдается в точках, где Волновое число k связано с длиной волны по формуле
С учетом этого условие интерференционного максимума:
Амплитуда результирующего колебания минимальна в точках, где
Волновое число k связано с длиной волны по формуле
С учетом этого условие интерференционного минимума:
Интерференция волн приводит к перераспределению энергии колебаний между соседними областями среды. Однако в среднем для большой области пространства энергия результирующей волны равна сумме энергий интерферирующих волн. Этот результат — следствие закона сохранения и превращения энергии.
Стоячие волны Частным случаем интерференции волн являются стоячие волны. Стоячей волной называется волна, образующаяся в результате наложения двух бегущих синусоидальных волн, которые распространяются навстречу друг другу и имеют одинаковые частоты и амплитуды. Стоячая волна образуется, например, пи отражении от преград. Падающая на преграду волна и бегущая ей навстречу отраженная волна, налагаясь друг на друга, дают стоячую волну.
Пусть две плоские волны с одинаковыми амплитудами и частотами распространяются навстречу друг другу вдоль х: Сложив вместе эти уравнения и преобразовав результат по формуле для суммы косинусов
получим уравнение результирующего колебания двух плоских волн (уравнение стоячей волны)
В точках, координаты которых удовлетворяют условию
амплитуда колебаний достигает максимального значения (т.к.  ). Точки среды, в которой амплитуда достигает своего максимального значения, называется пучностями стоячей волны. ). Точки среды, в которой амплитуда достигает своего максимального значения, называется пучностями стоячей волны.
На рис. 17.5. представлен характер движения различных точек натянутой упругой нити при установившейся в ней поперечной стоячей волне. Из условия (17.6.2) следует, что координата пучности
При этом следует иметь в виду, что пучность представляет собой не отдельную точку, а плоскость, точки которой имеют значения, определяемые формулой (17.6.3). В точках координаты, которых удовлетворяют условию
амплитуда колебаний равна нулю (т.к. Из условия (17.6.4) следует, что координата узла стоячей волны
Узел, так же как и пучность представляет собой не одну точку, а плоскость, точки которой имеют значения координаты, определяющие формулой (17.6.5). Расстояния между двумя соседними узлами и между двумя соседними пучностями одинаковы и равны половине длины бегущих волн. Эту величину называют длиной стоячей волны: λСТ = λ /2. В таблице 1 приведен сравнительный анализ основных характеристик бегущей и стоячей волн.
Таблица 1.
Образование стоячих волн наблюдается при интерференции бегущей и отраженной волн. Если среда, от которой происходит отражение, менее плотная, то на границе сред образуется пучность. Если среда, от которой происходит отражение, более плотная, то на границе сред образуется узел стоячей волны.
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 570; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.94.174 (0.008 с.) |






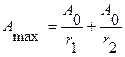
 , m- любые целые числа (0,1,2,3,…..), называемые порядком интерференционного максимума
, m- любые целые числа (0,1,2,3,…..), называемые порядком интерференционного максимума







 (17.6.1)
(17.6.1)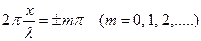 (17.6.2)
(17.6.2)
 (17.6.3)
(17.6.3)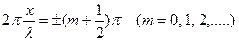 (17.6.4)
(17.6.4) ). Точки среды, в которой амплитуда достигает своего минимального значения, называется узлами стоячей волны (рис.17.5).
). Точки среды, в которой амплитуда достигает своего минимального значения, называется узлами стоячей волны (рис.17.5). (17.6.5)
(17.6.5)


