
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 17. Механические волны
Волновые процессы. Продольные и поперечные волны. Уравнение бегущей волны. Фазовая скорость. Волновое уравнение. Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды создать колебания ее частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с некоторой скоростью υ. Процесс распространения колебаний в пространстве называется волной. Среди разнообразия волн, которые встречаются в природе и технике можно выделить упругие и электромагнитные волны. Упругие волны - волны, которые распространяются в любой упругой среде. Электромагнитные волны - это волны, которые распространяются в электромагнитном поле. При распространении волны частицы колеблются около своих положений равновесия, а не перемещаются вслед за волной. Вместе с волной передается от частицы к частице лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн является перенос энергии без переноса вещества. В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. Продольная волна - волна, в которой частицы среды колеблются вдоль направления распространения волны. Поперечная волна – волна, в которой частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Продольные волны могут распространяться в средах, в которых возникают упругие силы при деформации сжатия и растяжения (в твердых, жидких и газообразных телах).
Поперечные волны могут распространяться только в среде, в которой возникают упругие силы деформации сдвига (только в твердых телах). На рис. 17.1. изображена кривая (график волны), которая дает смещение ξ из положения равновесия точек с различными х в некоторый момент времени. Отличие графика волны от графика гармонического колебания: 1) график волны представляет зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени ξ= ξ(x,t=const); 2) график гармонического колебания это зависимость смещения данной частицы от времени ξ= ξ(x =const, t); Длиной волны λ называется расстояние между ближайшими частицами, колеблющимися в одинаковой фазе. Длина волны λ равна расстоянию, на которое распространяется волна за время, равное периоду колебаний Т частиц среды:
λ= υT, λ· ν = υ где ν = 1/Т - частота колебаний, υ – скорость распространения волны. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны (или волновым фронтом). Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновых поверхностей существует бесконечное множество, в то время как волновой фронт каждый момент времени только один. Волновая поверхность, на которой колебание находится в максимальной фазе, называется гребнем волны.
Уравнение бегущей волны Бегущими волнами называются волны, которые переносят энергию в пространстве. Основной характеристикой бегущей волны является плотность потока энергии переносимой данной волной. Важными примерами бегущих волн является плоская и сферическая волны. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, в сферической волне — множество концентрических сфер. Уравнением бегущей волны – называется зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при прохождении в ней рассматриваемой волны. Найдем вид функции ξ в случае бегущей волны, предполагая, что колебания носят гармонический характер. Для упрощения направим оси координат так, чтобы ось х совпала с направлением распространения волны. Тогда волновые поверхности будут перпендикулярными к оси х и, поскольку все точки волновой поверхности колеблются одинаково, смещение ξ будет зависеть только от х и t: ξ = ξ{х, t). Пусть колебания точек, лежащих в плоскости х =0 (рис.17.2.), имеют вид x(0, t)= А соs(w t +a), Найдем вид колебания точек в плоскости, соответствующей произвольному значению X. Для того чтобы пройти путь от плоскости х = 0 до этой плоскости, волне требуется время τ =x/υ
где υ — скорость распространения волны. Следовательно, колебания частиц, лежащих в плоскости х, будут отставать по времени на τ от колебаний частиц в плоскости х = 0, т. е. будут иметь вид
Выражение (17.2.1) является уравнением плоской волны (и продольной и поперечной), распространяющейся в направлении х, где А=const - амплитуду волны; α - начальная фаза волны (определяется выбором начал отсчета х и t); Если ввести волновое число: Придем к следующему уравнению плоской волны, распространяющейся вдоль оси х: x(x, t)= А соs (w t- kx +a). (17.2.2) или в экспоненциальной форме: Зафиксируем какое-либо значение фазы, стоящей в уравнении волны (17.2.2)
Продифференцировав данное выражение, получим:
Таким образом, скорость распространения волны в этом уравнении, есть скорость перемещения фазы, в связи с чем, ее называют фазовой скоростью. Волновое уравнение Распространение волн в общем случае описывается волновым уравнением – дифференциальным уравнением в частных производных. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и времени от функции (17.2.2), описывающую бегущую волну:
Сравнивая уравнения (17.3.1) и (17.3.2), можно записать
Следовательно, производные по координатам x,y и z
Сложив производные по координатам
Используя, оператор Лапласа
волновое уравнение примет вид
Решением волнового уравнения является уравнение любой волны (в том числе и плоская и сферическая волны).
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.221.67 (0.006 с.) |

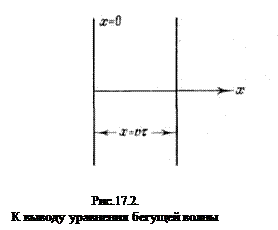
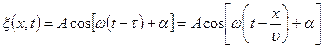 (17.2.1)
(17.2.1) -фаза плоской волны.
-фаза плоской волны.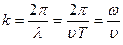 ,
,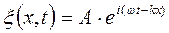
 или (w t- kx +a)=const
или (w t- kx +a)=const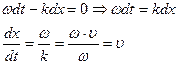
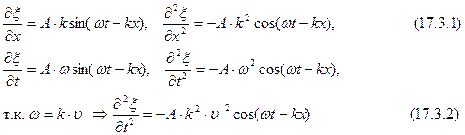

 ,
, 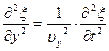 ,
, 

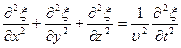 - волновое уравнение для плоской волны
- волновое уравнение для плоской волны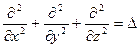
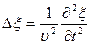 .
.


