
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Затухающие колебания. Логарифмический декремент затухания.
В реальном случае на колеблющееся тело действуют силы сопротивления (трения), характер движения изменяется и колебание становится затухающим. При не очень больших амплитудах и частотах эта сила трения пропорциональна скорости и направлена в противоположную сторону движения:
где Тогда уравнение движения, согласно второму закону Ньютона
Обозначим
Тогда
Подстановка в (15.4.2, б) функции х = e λ t приводит к характеристическому уравнению
Корни этого уравнения равны
При не слишком большом затухании (при β<ω0) подкоренное выражение будет отрицательным. Представим его в виде (iω)2, где ω - величина, равная
Тогда корни характеристического уравнения запишутся следующим образом:
при не слишком сильном затухании общее решение уравнения (15.4.2,б) имеет вид
где А 0 - амплитуда колебаний в начальный момент времени.
На рисунке дан график (15.4.) затухающих колебаний. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки x. В соответствии с видом функции (15.4.7) движение системы можно рассматривать как гармоническое колебание частоты ω с амплитудой, изменяющейся по закону А (t) = А 0 e ‑β∙ t . Скорость затухания колебаний определяется величиной β = b /2 m, которую называют коэффициентом затухания. Найдем время τ, за которое амплитуда уменьшается в e раз. По определению e ‑β∙τ = e ‑1, откуда β∙τ = 1. Следовательно, коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда уменьшается в e раз. Период затухающих колебаний равен
При незначительном сопротивлении среды Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно
Это отношение называют декрементом затухания, а его логарифм — логарифмическим декрементом затухания:
Логарифмический декремент характеризует затухание колебаний за период. Пусть
Таким образом,
Вынужденные колебания.
Для получения незатухающих колебаний необходимо воздействовать дополнительной переменной внешней силой, которая бы восполняла убыль энергии. Колебания системы, которые совершаются за счет работы периодически меняющейся внешней силы, называются вынужденными. Рассмотрим движение пружинного маятника массой т под действием периодически вынуждающей силы F/ (рис. 15.5). Пусть вынуждающая сила изменяется со временем по гармоническому закону
Тогда уравнение движения запишется следующим образом:
Разделим уравнение на m и введем обозначения
получим неоднородное линейное дифференциальное уравнение второго порядка:
где b - коэффициент затухания, Как известно из теории дифференциальных уравнений, общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. Общее решение однородного уравнения имеет следующий вид:
где А0 и Y - произвольные постоянные. Найдем частное (не содержащее произвольных постоянных) решение уравнения в виде
и определим значения А и j, при которых данная функция удовлетворяет уравнению (15.5.1). Найдем производные
Подставим (15.5.3), (15.5.4) и (15.5.5) в уравнение (15.5.1):
Учитывая, что
получим:
Для того, чтобы уравнение (15.5.6) удовлетворялось при всех значениях t, необходимо, чтобы коэффициенты при sinwt и coswt в левой и правой частях уравнения были одинаковы. Отсюда следуют два уравнения:
Возводя в квадрат и складывая, их друг с другом, получим:
Из (15.5.9) следует, что амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы (F0) и зависит от ее частоты (w).
Из уравнения (15.5.8) найдем сдвиг фаз:
т.е. вынужденные колебания сдвинуты по фазе относительно вынуждающей силы, причем величина сдвига фаз j зависит от частоты вынуждающей силы. Подставляя (15.5.9) и (15.5.10) в уравнение (15.5.3), получим частное решение неоднородного уравнения:
Функция (15.5.11) в сумме с (15.5.2) дает общее решение уравнения (15.5.1), которое описывает поведение системы при вынужденных колебаниях. Слагаемое (15.5.2) играет заметную роль только в начальной стадии процесса, с течением времени из-за экспоненциального множителя е-βt роль слагаемого (15.5.2) уменьшается и через некоторое время им можно пренебречь, сохраняя в решении слагаемое (15.5.11). Таким образом, функция (15.5.11) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы (15.5.9) приводит к тому, что при некоторой, определенной для данной системы частоте, амплитуда колебаний достигает максимального значения. Резкое увеличение амплитуд вынужденных колебаний в области, где частота
Уравнение (15.5.12) имеет три решения:
Таким образом, резонансная частота будет определяться по формуле:
Подставив это значение частоты в (15.5.9), получим выражение для амплитуды при резонансе:
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы изображается графически (рис.15.6) и называется резонансной кривой. При w®0 из уравнения (15.5.9) следует, что
т.е. при w®0 все кривые приходят к одному и тому же предельному значению
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 817; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.64.226 (0.025 с.) |
 , (15.4.1)
, (15.4.1) – коэффициент трения, характеризующий свойства среды оказывать сопротивление.
– коэффициент трения, характеризующий свойства среды оказывать сопротивление. (15.4.2)
(15.4.2) (15.4.2, а)
(15.4.2, а)

 (15.4.2, б)
(15.4.2, б) (15.4.3)
(15.4.3) ,
,  . (15.4.4)
. (15.4.4) . (15.4.5)
. (15.4.5) ,
,  . (15.4.6)
. (15.4.6)
 , (15.4.7)
, (15.4.7)
 . (15.4.8)
. (15.4.8) , период колебаний практически равен T 0 = 2π/ω0. С ростом коэффициента затухания период колебаний увеличивается.
, период колебаний практически равен T 0 = 2π/ω0. С ростом коэффициента затухания период колебаний увеличивается. .
. (15.4.9)
(15.4.9) – число колебаний, после которых амплитуда уменьшается в e раз, а
– число колебаний, после которых амплитуда уменьшается в e раз, а  - промежуток времени, соответствующий этому уменьшению. Тогда
- промежуток времени, соответствующий этому уменьшению. Тогда  ,
,  ,
,  и
и ,
, .
. – есть величина, обратная числу колебаний, по истечении которых амплитуда спадает в e раз. Например, если
– есть величина, обратная числу колебаний, по истечении которых амплитуда спадает в e раз. Например, если  это значит, что амплитуда колебаний уменьшается в e раз по истечении 100 колебаний. Зная
это значит, что амплитуда колебаний уменьшается в e раз по истечении 100 колебаний. Зная  (15.4.10)
(15.4.10)
 .
. .
. ,
,  ,
,  ,
,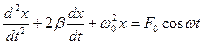 , (15.5.1)
, (15.5.1) - собственная частота колебаний системы.
- собственная частота колебаний системы. , (15.5.2)
, (15.5.2) ,
, (15.5.3)
(15.5.3) ; (15.5.4)
; (15.5.4) . (15.5.5)
. (15.5.5)
 ,
,
 (15.5.6)
(15.5.6) ; (15.5.7)
; (15.5.7) . (15.5.8)
. (15.5.8) ,
, . (15.5.9)
. (15.5.9) ;
; , (15.5.10)
, (15.5.10) . (15.5.11)
. (15.5.11)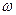 близка к частоте собственных колебаний системы
близка к частоте собственных колебаний системы  , называется резонансом, а соответствующая частота - резонансной частотой. Чтобы определить резонансную частоту wрез, нужно найти максимум функции или минимум выражения, стоящего под корнем в знаменателе формулы (15.5.9). Продифференцируем это выражение по w и, приравняв нулю, получим:
, называется резонансом, а соответствующая частота - резонансной частотой. Чтобы определить резонансную частоту wрез, нужно найти максимум функции или минимум выражения, стоящего под корнем в знаменателе формулы (15.5.9). Продифференцируем это выражение по w и, приравняв нулю, получим: . (15.5.12)
. (15.5.12)
 .
. .
.

 ,
, . Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной величины F. Чем меньше b, тем сильнее изменяется с частотой амплитуда, тем острее получается максимум. При стремлении w®¥ все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия.
. Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной величины F. Чем меньше b, тем сильнее изменяется с частотой амплитуда, тем острее получается максимум. При стремлении w®¥ все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия.


