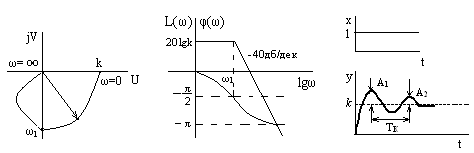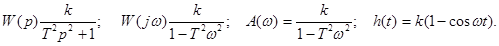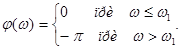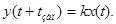Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотные и временные характеристики звеньевСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Частотные характеристики звеньев (системы) получают путем подачи на вход гармонического сигнала с постоянной амплитудой и переменной частотой от нуля до ∞, при этом замеряя на выходе амплитуду и фазу сигнала. Подставим в ПФ звена s = jω
где Экспериментально для построения амплитудно-фазовой частотной характеристики или годографа требуются в генератор частоты, вольтметр и частотомер. Для построения логарифмических амплитудно-частотных характеристик используется выражение L(ω) = 20 lg A(ω). По оси абсцисс откладываются частоты, выраженные в логарифмах lg ω, подекадно: 1, 10, 100…. или в логарифмах 0, 1, 2 … Временная характеристика звена (системы) определяется переходной функцией h(t) или кривой разгона, описывающей реакцию звена (системы) на единичный входной сигнал 1(t)
Импульсной переходной или весовой функцией ω(t) звена (системы) называют функцию, описывающую реакцию на единичное импульсное воздействие или дельта функции Импульсная переходная функция и переходная функция связаны выражением
3.2.1 Пропорциональное (усилительное) звено
Типовое уравнение взаимосвязи выходного и входного сигналов пропорционального звена является алгебраическим: y(t) = k х(t).
ПФ пропорционального звена имеет вид Аналитическое выражение вектора АФХ этого звена W(jω) = k, из которого видно, что ПФ не зависит от частоты входного сигнала. A(ω) = k; φ(ω) = arctg 0 = 0; L(ω) = 20 lg k.
Рисунок 3.1 – Частотные и временные характеристики пропорционального звена Поскольку АФХ пропорционального звена не зависит от частоты ω, годограф ее вектора лежит на действительной полуоси комплексной плоскости на расстоянии k от начала координат (рис.3.1). Пропорциональное звено мгновенно (без инерции) реагирует на возмущающее воздействие. По типовой кривой разгона видно, что выходной сигнал пропорционален входному и ордината выходного сигнала равна коэффициенту пропорциональности k. 3.2.2 Астатическое (интегрирующее) звено Типовое дифференциальное уравнение этого звена имеет вид
Операторная форма записи дифференциального уравнения Т р у (р) = k х(р).
Передаточная функция имеет вид
Из ПФ путем замены р = jω получается аналитическое выражение вектора АФЧХ астатического звена: При изменении частоты ω от 0 до ∞ конец вектора АФЧХ перемещается по отрицательной мнимой полуоси комплексной плоскости, т.к. действительная часть вектора АФЧХ равна нулю.
По кривой разгона видно, что объект, аппроксимируемый астатическим звеном, не обладает свойством самовыравнивания. По кривой разгона можно определить коэффициент постоянную времени Т в ПФ астатического звена: Т = 1/ tgα = ctgα.
Рисунок 3.2 – Частотные и временные характеристики астатического звена Примером реализации астатического ТДЗ является бункер накопитель в технологической цепи производства. Объекты, которые описываются астатическим (интегрирующим) звеном, называют астатическими. Такие объекты не обладают свойством самовыравнивания. 3.2.3Дифференцирующее звено
Дифференциальное уравнение дифференцирующего звена имеет вид
Операторная форма записи этого уравнения ПФ дифференцирующего звена имеет вид
Аналитическое выражение вектора АФЧХ такого звена Годограф этого звена показан на (рис.3.3). Конец вектора АФЧХ перемещается из начала координат по положительной мнимой полуоси, уходя при ω=∞ в бесконечность. Типовая кривая разгона дифференцирующего звена своеобразна: выходной сигнал пропорционален первой производной входного сигнала, т.е. тангенсу угла наклона вектора АФЧХ. В момент подачи входного воздействия этот угол равен +900, а tg(+900) = +∞, но далее входное воздействие устанавливается равным единице, при этом угол наклона становится равным -900, а tg(-900) = - ∞. Следовательно, выходной сигнал в момент подачи входного воздействия принимает значение +∞. Тут же из +∞ вычитается - ∞ и выходной сигнал возвращается в исходное нулевое состояние.
Рисунок 3.3 – Частотные и временные характеристики дифференцирующего звена Примером реализации дифференцирующего звена может быть электрическая RС цепь, состоящая из конденсатора и резистора.
3.2.4 Апериодическое (инерционное, статическое) звено первого порядка
Дифференциальное уравнение апериодического звена первого порядка имеет вид
а операторная форма записи – изображение этого уравнения
Из этого выражения можно получить передаточную функцию
Примером ПФ апериодического звена может служить фильтр низкой частоты на RC или RL элементах.
После необходимых преобразований получим
Изменяя частоту ω от 0 до ∞, можно построить годограф (рис.3.4), представляющий собой полуокружность, расположенную в четвертом квадранте комплексной плоскости, диаметр которой равен коэффициенту k.
Рисунок 3.4 – Частотные и временные характеристики апериодического звена 1 порядка В ЛАЧХ амплитуда ПФ остается постоянной и равной 20lgk до частоты ω1 = 1/Т называемой сопрягаемой частотой, после нее происходит уменьшение амплитуды через каждую декаду на 20 децибел (-20 дб/дек). Частота, при которой амплитуда ПФ равна единицы, называется частотой среза ωс А(ωс) = 1, после которой система теряет усилительные свойства A(ω) < 1. Кривая разгона апериодического звена имеет форму экспоненты. Если к любой ее точке провести касательную, а затем точку касания и точку пересечения касательной с асимптотой, спроецировать на ось времени, то получится один и тот же отрезок на оси времени. Эта проекция, называемая постоянной времени, соответствует коэффициенту Т в передаточной функции. Таким образом по кривой разгона легко найти коэффициента k и Т в передаточной функции апериодического звена. Примером реализации апериодического звена является электродвигатель небольшой мощности, который после включения в электросеть (подачи единичного скачка) набирает обороты по экспоненте. Объекты с передаточной функцией апериодического звена называют статическими.
3.2.5 Форсирующее звено 1 порядка
При моделировании систем приходится сталкиваться со звеньями, которые не входят в разряд типовых, но которые оказывают отрицательное влияние на устойчивость. К ним относятся форсирующие 1 и 2 порядков, консервативное и неминимально-фазовые звенья. Форсирующее звено 1 порядка напоминает апериодическое звено 1 порядка, но ПФ и частотные свойства противоположные. W(p) = k (Tp +1). Для построения годографа поставим в ПФ p = jω и получим W(jω) = k (1 + jTω).
Изменяя частоту ω от 0 до ∞, строится годограф (рисунок 3.5), представляющий собой прямую параллельную мнимой положительной полуоси и расположенную во втором квадранте комплексной плоскости.
Рисунок 3.5 – Частотные характеристики форсирующего звена 1 порядка
Как видно их частотных характеристик после сопрягаемой частоты ω1 = 1/Т амплитуда ПФ резко возрастает и звено (система) становится неустойчивой, т.е. такие звенья применять в структурной схеме нежелательно.
3.2.6 Апериодическое звено 2-го порядка
Дифференциальное уравнение этого звена имеет вид В операторной форме записи (Т1р2 + Т2 р + 1) у (р) = k х(р) или
где
Передаточная функция имеет вид Существуют три вида апериодических звеньев 2 порядка в зависимости от величины коэффициента демпфирования ξ: а) ξ ≥ 1 – апериодическое звено 2 порядка; б) 0 < ξ < 1 – колебательное звено; в) ξ = 0 – консервативное звено.
А. Апериодическое звено 2 порядка (ξ ≥ 1)
ПФ звена преобразуется как два последовательно соединенных апериодических звена 1 порядка.
где Таким образом, апериодическое звено 2 порядка при ξ ≥ 1 ведет себя также как и 2 апериодических звена 1 порядка. Поэтому АФЧХ и ФЧХ аналогичны звену первого порядка, но с наклоном ЛАЧХ при ω1 = 1/Т1 -20 дб/дек и затем при ω2 = 1/Т2 еще раз -20дб/дек. Общий наклон составит - 40дб/дек.
Б. Колебательное звено (0 < ξ < 1)
Подставив р = jω в ПФ звена, получим
Фазо-частотная характеристика звена имеет следующие значения
Решив дифференциальное уравнения звена при х(t) =1 при нулевых начальных условиях, получим переходную функцию h(t) или кривую разгона
где
Рисунок 3.6 – Частотные и временные характеристики колебательного звена По кривой разгона можно вычислить постоянную времени Т и ξ колебательного звена. Измерив период колебаний Тк и амплитуды колебаний А1 и А2 на кривой разгона, находят коэффициенты α и β по формулам
Подставив рассчитанные значения коэффициентов α и β в (3.1) и решая систему уравнений с двумя неизвестными, определяются Т и ξ. Объекты, описываемые колебательным звеном, обладают свойством самовыравнивания, т.е. способностью самостоятельно восстанавливать состояние равновесия после возмущающего воздействия.
В. Консервативное звено (ξ = 0) ПФ звена равна
Фаза ПФ звена при различных значениях частоты имеет вид
Рисунок 3.7 – Частотные и временные характеристики консервативного звена
Как видно из ЛАЧХ при сопрягаемой частоте амплитуда ПФ стремится к бесконечности, т.е. происходит явление резонанса. Переходная характеристика убеждает в нежелательности применения этого звена, т.к. при подаче единичного воздействия возникают незатухающие колебания.
3.2.7 Форсирующее звено 2 порядка
ПФ форсирующего звена 2 порядка имеет вид
а) при ξ ≥ 1 W(p) = k (T1p + 1)(T2p +1), где ПФ представляет собой 2 последовательно соединенных форсирующих звена 1 порядка. Поэтому АФЧХ и ФЧХ аналогичны звену первого порядка, но с наклоном ЛАЧХ при ω1 = 1/Т1 +20 дб/дек и затем при ω2 = 1/Т2 еще раз +20дб/дек. Общий наклон составит + 40дб/дек. б) при 0 ≤ ξ < 1 ЛАЧХ имеет наклон при ω1 = 1/Т +40дб/дек. Частотные свойства аналогичны как и у колебательного звена, но с противоположным знаком: годограф расположен в первом и во втором квадранте, а ФЧХ изменяется от 0 до +π.
3.2.8 Запаздывающее звено
Типовое уравнение взаимосвязи входного и выходного сигналов запаздывающего звена имеет вид
ПФ этого звена равна
Вектор АФЧХ этого звена имеет вид
Рисунок 3.8 – Частотные и временные характеристики запаздывающего звена Годограф запаздывающего звена представляет собой бесконечное число окружностей с единичным радиусом вокруг начала координат комплексной плоскости (рисунок 3.8). Первая окружность замыкается, когда ωtзап = 2π или при частоте ω = 2π/tзап.. Примером реализации этого звена может служить ленточный транспортер. Если на вход транспортера подать возмущение в виде единичного скачка, т.е. открыть подачу материала, то этот же единичный скачок появится на его выходе через отрезок времени, равный времени запаздывания.
3.2.9 Неминимально-фазовые звенья
Выше рассмотренные звенья относятся к минимально-фазовым. ПФ звена (системы) можно представить и как отношение полиномов входного и выходного сигналов комплексной переменной р
Характеристическим уравнением звена (системы) называется полином знаменателя ПФ звена (системы) Q(p). Корни числителя ПФ R(p) = 0 называются нулями zi, а знаменателя Q(p) = 0 называются полюсами рi. Минимально-фазовые звенья имеют отрицательные или равные нулю вещественные части Re pi и Re zi ≤ 0. Если хотя бы один нуль zi или полюс рi ПФ имеет положительную вещественную часть Re zi > 0 или Re pi > 0, то такое звено называется неминимально-фазовым, например:
Сдвиг фаз φ(ω) немимально-фазовых звеньев больше, чем у соответствующих минимально-фазовых звеньев. Рассмотрим АФЧХ немимально-фазового апериодического звена 1 порядка, ПФ которого имеет вид
Рисунок 3.7 – Частотные характеристики апериодического неминимально-фазового звена
Тема 4. АФЧХ и ЛАЧХ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.166.45 (0.008 с.) |


 - модуль ПФ;
- модуль ПФ;  - фаза ПФ или сдвиг фазы выходного сигнала.
- фаза ПФ или сдвиг фазы выходного сигнала.
 при нулевых начальных условиях.
при нулевых начальных условиях.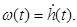



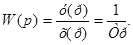





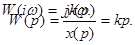
















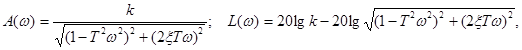

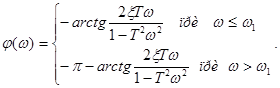
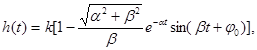
 (3.1)
(3.1)