
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость нестационарных систем
Линейными системами с переменными параметрами или нестационарными системами называют системы, процессы в которых описываются линейными дифференциальными уравнениями с переменными во времени коэффициентами [a0(t)pn + a1(t)pn-1 +.... + an(t)]Y(t) = [b0(t)pm + b1(t)pm-1 +.... + bm(t)]X(t), (7.14) где Y(t) и X(t) – выходная и входная величины; ai(t), bi(t) – переменные коэффициенты, являющиеся известными функциями времени и задаваемые либо графически, либо аналитически; p =d/dt – оператор дифференцирования. Для нестационарных систем понятие устойчивости имеет некоторую специфику. Действительно, если предположить, что входная величина системы x(t) = x0 = Const и к моменту времени t1 переходные процессы в системе закончились, т.е. если принять p = d/dt = 0, то из (8.14) для t > t1 имеем Y(t) = [bm(t)/an(t)]X0. (7.15) Из (7.15) видно, что в зависимости от характера изменения коэффициентов an(t) и bm(t) в нестационарной системе даже при постоянной входной величине Х0 выходная величина Y(t) может изменяться неограниченно долго. Так как время работы реальных систем ограничено, то установившегося значения в нестационарной системе за время ее работы не наблюдается и поэтому понятие асимптотической устойчивости теряет практический смысл. Точные методы исследования устойчивости нестационарных систем довольно сложны, поэтому на практике используются приближенные методы, например, метод замораживания коэффициентов. Он применим в тех случаях, когда нестационарная система работает только в течение ограниченного интервала времени Т, а коэффициенты (7.14) практически не изменяются за время переходного процесса в системе. В соответствии с этим методом для некоторого фиксированного времени t = tk определяют соответствующие ему значения ai(tk) и bi(tk) коэффициентов дифференциального уравнения (7.14), заменяют исходную нестационарную систему некоторой фиктивной стационарной САУ и исследуют устойчивость по любому критерию. Если полученная таким образом стационарная система устойчива, то считают, что исследуемая нестационарная система тоже устойчива в рассматриваемый момент времени. Затем проводят аналогичное исследование устойчивости для других фиксированных моментов времени, лежащих в интервале 0 ≤ t ≤ T, где Т – время работы. Если во всем рабочем интервале Т условия устойчивости стационарной системы, полученной методом замораживания коэффициентов, выполняются, то исходную нестационарную систему на этом интервале считают устойчивой.
Степень достоверности метода будет тем выше, чем меньше изменяются коэффициенты за время протекания переходного процесса, а также от правильного выбора фиксированных моментов времени, их количества, с тем чтобы охватить возможные варианты значений коэффициентов, в которых происходит значительное изменение, смена знака и т.д. В общем случае, когда коэффициенты уравнения (7.14) изменятся значительно, при 8сследовании устойчивости нестационарных систем пользуются понятием технической устойчивости или устойчивости на конечном интервале. Систему считают технически устойчивой на данном интервале Т, если выходная величина Y(t) не превышает некоторой заданной величины Yдоп при 0 ≤ t ≤ T. Yдоп выбирается в каждом конкретном случае из технических соображений (рисунок 7.5).
Рисунок 7.5 – Выходные величины нестационарных систем: 1,2 – технически устойчивая система; 3,4 – технически неустойчивая
Определение Y(t) производят обычно при заданном входном воздействии X(t) с помощью различных приближенных аналитических методов, либо методами математического моделирования (например, с помощью программы VisSim).
7.4 Контрольные вопросы
1) Какой критерий лежит в основе определения устойчивости по виду ЛАЧХ? 2) Чему равна ПФ запаздывающего звена? 3) Почему для определения устойчивости САУ с запаздыванием алгебраические критерии непригодны? 4) Что такое критическая частота ωкр системы с запаздыванием? 5) Что такое τкр для систем с запаздыванием? 6) Какие линейные системы называются нестационарными? 7) Как определяется устойчивость нестационарной системы? Лекция 8. Цифровые системы 8.1 Основные положения и определения
Система называется цифровой, если в контуре имеется хотя бы один цифровой элемент. Амплитудно-импульсная модуляция (АИМ) это модуляция, при которой амплитуда импульса модулированного сигнала У пропорциональна величине информационного сигнала Х, подаваемого на вход модулятора.
Существует 2 вида АИМ: первого и второго рода. В АИМ 1-го рода амплитуда модулированного сигнала в течение длительности импульса τ повторяет информационный сигнал Х. При АИМ 2-го рода амплитуда импульса в течение длительности импульса τ постоянна. Например, в АЦП используется АИМ 2-го рода.
Рисунок 8.1 – Виды АИМ В АЦП преобразование происходит в 2 этапа: дискретизация по времени с периодом Т и квантование по уровню аналогового сигнала. Поэтому блок АЦП можно представить в виде 2-х элементов: импульсного элемента, осуществляющего дискретизацию по времени и формирователя импульсов, выполняющий квантование по уровню (рисунок 8.2,а). Цифровая система (ЦС), содержащее АЦП, приведена на рисунке 8.2,б.
Рисунок 8.2 – Структурная схема ЦС с АЦП При увеличении разрядности АЦП (числа квантований) ошибка между значением цифрового сигнала и аналогового уменьшается.
8.2 Z-преобразование
Для описания ЦС используется z-преобразование. Для этого необходимо перейти из области t в область р, а затем в область Z. Преобразование Лапласа имеет вид
Приближенно интеграл можно представить в виде суммы
Примем
Пример 1. Найти z-изображение
В правой части уравнения сумма бесконечно убывающей геометрической прогрессии, знаменатель которой равен
Тогда
Таблица 8.1 – Примеры перехода из t в Z и P области
Пример 2. Дана x(t) = 1(t). Требуется получить z-изображение другим способом. Как и при первом способе, получим изображение единичной функции в виде ряда Тейлора x(z) = 1 + z-1 + z-2 +…..+z-n. Умножим на z-1 обе части уравнения x(z) ∙ z-1 = z-1 + z-2 + z-n-1, и вычтем из первого выражения x(z), полученное x(z) ∙ z-1. Тогда x(z) – x(z) ∙ z-1 = 1. Отсюда
Пример 3. Дана функция x(t)= t ∙ 1(t). Получить z-изображение.
x(z) ∙ z-1 = Tz-2 + 2Tz-3 + …;
8.3 Теоремы Z- преобразования
1) Суммирование и вычитание. Если f1(t) и f2(t) имеют z-преобразование, то
2) Умножение на константу. Если f(t) имеет z- преобразование F(z), то
3) Сдвиг во временной области. Если f(t) имеет z- преобразование F(z), то
Пример 4. Найти z- преобразование единичной ступенчатой функции 1(t) при задержке ее на один период квантования Т.
4) Об умножении оригинала на экспоненту (смещение в области изображений). Если f(t) имеет изображение f(z), то
5) Теорема о начальном значении. Если f(t) имеет z- преобразование F(z) и если существует предел
Из теоремы следует, что значение дискретного сигнала f(t) при t=0 определяется значением F(z) при z = ∞. 6) Теорема о конечном значении. Если f(t) имеет z-преобразование F(z) и если функция (1-z-1)F(z) не имеет полюсов на окружности единичного радиуса
Пример 5. Найти конечное значение f(nT) для заданного z-преобразования
Приведем заданную функцию к виду
Определим корни знаменателя, т.е. определим полюса ПФ. Поскольку функция не имеет полюсов на единичной окружности, то
7) Теорема дифференцирования. Если z-преобразование функции f(t,a) есть F(z,a), где а – независимая переменная или константа, то
Пример 6. Определить z-преобразование функции f(t) = te-αt с помощью теоремы дифференцирования.
8.4 Обратное z- преобразование
Преобразование Лапласа и его обратное преобразование для непрерывных функций является однозначным. Для z-преобразования обратное z-преобразование не является однозначным. Корректный результат обратного z-преобразования функции F(z) есть f(nT), который равен f(t) только в моменты t = nT. Рисунок 8.3 иллюстрирует тот факт, что для z-преобразования единичной ступенчатой функции, которое равно z/(z - 1) и соответствует последовательности единичных импульсов. Обратное z-преобразование может быть любой функцией, значения которой равны единицы в моменты t=0,T,2T. Неоднозначность обратного z-преобразования является одним из ограничений этого метода.
Рисунок 8.3 – Решетчатая функция ЦС Обратное z-преобразование осуществляет переход от z-изображения к решетчатой функции и обозначается как
Обратное z-преобразование может быть определено методом разложения на простые дроби. Этот метод близок к методу разложения на простые дроби в преобразовании Лапласа. При анализе непрерывных систем обратное преобразование Лапласа F(p) может быть получено разложением в виде
где а, в, с – отрицательные полюсы F(p); А, В, С – вычеты F(p) в этих полюсах. Тогда в соответствии с таблицей 1.2 можно осуществить переход к оригиналу
Для случая z-преобразования F(z) не надо представлять в форме (8.2), поскольку в таблице 8.2 обратное z-преобразование для выражений типа A/(z + a) отсутствует. Вместе с тем из таблицы 8.2 видно, что обратное z-преобразование функции Az/(z – e-at) равно Ae-anT. Следовательно, удобнее разложить на простые дроби функцию F(z)/z. После разложения обе части выражения для F(z)/z умножают на z для получения F(z). Пример 7. Дано z-изображение, имеющее вид
Разложим по (8.2) на слагаемые
В соответствии с таблицей 1.2 определяется оригинал функции
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.22.244 (0.027 с.) |




 - решетчатая функция. Например,
- решетчатая функция. Например,  .
. - разностное уравнение 1-го порядка;
- разностное уравнение 1-го порядка; - разностное уравнение 2-го порядка;
- разностное уравнение 2-го порядка; - разностное уравнение k-го порядка.
- разностное уравнение k-го порядка. .
.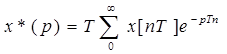 .
. , тогда
, тогда или
или . (8.1)
. (8.1) .
.
 .
. .
.




 .
.



 , то
, то
 или вне ее, то
или вне ее, то .
.





 .
. , (8.2)
, (8.2) .
. .
. ;
; 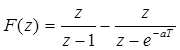 .
. .
.


