
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация САУ и законы управленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тема 1. Основные понятия и принципы управления 1.1 Основные термины и определения
В теории автоматического управления рассматриваются вопросы анализа и синтеза систем автоматического управления с заданными требованиями по качеству на основе методов и специального математического аппарата. Поэтому необходимо ознакомиться с основными терминами и определениями. Система автоматического управления(САУ) – это совокупность технических средств для управления регулируемым параметром, в которой вычисление сигналов управления осуществляется регулятором или программируемым контроллером. Объект управления(ОУ) – это установка, в которой протекающие физические процессы, управляются (регулируются) с помощью специальных технических средств. Регулируемый параметр – это технологический параметр, значением которого управляют с помощью специальных технических средств. Воздействия – внешние факторы, изменяющие течение технологического процесса в объекте управления. Различают возмущающие и управляющие воздействия. Возмущающиевоздействия носят случайный характер. Например, изменение температуры окружающей среды, давления, скорости воздуха, колебания напряжения в электросети. Управляющие воздействия на объект управления организуются техническим устройством в САУ для компенсации возмущающих воздействий. Под сигналами понимают совокупность энергии или вещества, поступающего в объект управления, возмущающие и управляющие воздействия, а также регулируемые параметры. По направлению различают входные х и выходные у сигналы объекта управления (рисунок 1.1). Так, возмущающие и управляющие воздействия будут входными сигналами для объекта управления; регулируемый же параметр всегда принимают за выходной сигнал, даже если он физически за пределы объекта не выходит (например, уровень жидкости в емкости, напряжение на обмотках электродвигателя). На схемах (рисунок 1.1) функциональные элементы САУ обозначают прямоугольником, а сигналы – стрелками.
Рисунок 1.1 - Функциональный элемент САУ
Параметры физических процессов, определяющие сигналы, содержат информацию. Например, с помощью электрических сигналов в связи передаются звуки, а в телевидении изображения. Параметры, содержащие информацию, называются информационными. Так, сигналом является электрическое напряжение, информационным параметром – амплитуда этого сигнала. Для примера рассмотрим технологический процесс регулирования температуры в электропечи для закаливания металла (рисунок 1.2). Функциональной схемой называется символическое изображение элементов технологического процесса и связей между ними, отражающее последовательность процессов в системе. Данная система предназначена для поддержания необходимого режима, т.е. изменения температуры х(t)в электропечи по заданному закону. Для обеспечения требуемого процесса электропечь снабжается: термопарой (датчик), с выхода которой получают электрическое напряжение у(t), пропорциональное температуре в электропечи, и реостатом, с помощью которого меняется сопротивление в цепи ее нагрева. Отклонение фактической температуры в электропечи от заданной не должно превышать допустимого значения ε(t). В системе имеет место так называемая обратная связь (ОС). Сигнал х(t)заданной температуры в печи называют управляющим, сигнал у(t) фактической температуры – управляемой переменной, а систему, реализующую процесс закаливания, - системой автоматического управления (рисунок 1.3). САУ представляет собой совокупность объекта управления и управляющего устройства: регулятор, усилитель, электродвигатель, реостат, датчик и элемент сравнения. Объект управления - электропечь, а управляемая выходная переменная – температура. Управляющее устройство выполняет целенаправленно действия, приводящие к заданному изменению управляемой переменной - температуры закаливания. В зависимости от значения и знака сигнала рассогласования ε(t) регулятор посредством привода уменьшает или увеличивает сопротивление на реостате, тем самым поддерживая заданную температуру печи. Регулятор вырабатывает команды управления u(t).
Рисунок 1.2 - Функциональная схема системы процессом закаливания металла: 1- задающее устройство; 2 – сравнивающее устройство; 3 – регулятор; 4 – усилитель мощности; 5 – привод электродвигателя; 6 – реостат; 7 – электропечь; 8 – датчик Данная САУ является замкнутой системой, в которой имеет место обратная связь (ОС), т.е. сравнение входного сигнала (эталона) с выходным (фактическим значением регулируемой величины). Теория автоматического управления – это наука об анализе и синтезе автоматических систем с заданными требованиями по качеству на основе методов и специального математического аппарата.
Цели и принципы управления Задача управления – изменять протекающие в объекте управления процессы посредством соответствующих команд для достижения поставленной цели. Фундаментальными принципами управления являются: - принцип разомкнутого управления; - принцип компенсации – управление по возмущению; - принцип обратной связи. Таким образом, САУ – это система, стремящаяся сохранить в допустимых пределах рассогласование (ошибку) ε(t) между требуемыми х(t) и действительными у(t) значениями управляемых переменных с помощью их сравнения на основе принципа ОС и использования получаемых при этом сигналов управления. Система, в которой входной сигнал х(t) – известная функция (детерминированный сигнал) на всем промежутке управления, называется системой программного управления. Система, в которой задающий входной сигнал х(t) =const, называется системой стабилизации. Система, в которой задающее входной сигнал x(t)– случайная функция, называется следящей системой. Система, управляющая только одной выходной величиной, называются одномерной. Одномерные системы могут быть системами программного управления, системами стабилизации и следящими системами. Кроме того, на практике используются: - системы с поиском экстремума показателя качества; - системы оптимального управления; - адаптивные системы.
Математические модели САУ
На первом этапе расчета и проектирования САУ ограничиваются их качественным описанием на основе анализа функциональных схем, т.е. неформальным описанием. Неформальным описанием называется совокупность сведений о САУ, достаточных для построения алгоритма ее работы, т.е. для построения функциональной схемы, служащей основой для разработки ее формального (математического) описания. Недостаток неформального описания САУ состоит в том, что в этом случае не оперируют количественными характеристиками и, таким образом не достигается необходимая точность. Под математической моделью САУ понимают количественную формазизацию абстрактных представлений об изучаемой системе. Математическая модель – это формальное описание системы с помощью дифференциальных, интегральных, разностных, алгебраических уравнений, а также неравенств, множеств и т.д. Пусть У и Х – множества входных и выходных сигналов САУ. Если каждому элементу у є У ставится в соответствие определенный элемент х є Х, то говорят, что задан системный оператор А, посредством которого задается связь между входом и выходом САУ: у = Ах; (1.1) Операторное уравнение (1) следует считать математическим уравнением САУ, поскольку оно устанавливает количественную связь между ее входным х(t) и выходным у(t) сигналами. Задать оператор системы - значит задать правило определения ее выходного сигнала по входному сигналу. В большинстве случаев операторные уравнения систем принадлежат к классу дифференциальных уравнений или эквивалентных им интегральных уравнений. Для получения дифференциального уравнения системы в целом обычно описывают отдельные элементы, т.е. составляют дифференциальные уравнения для каждого входящего в систему элемента: элемента сравнения, регулятора, усилителя, привода, датчика и т.д. (рисунок 1.2).
Рисунок 1.3 - Структурная схема САУ по отклонению
САУ по возмущению – принцип Ж.Понселе, предложеннй им в 1830г. Если f возмущающее действие на объект, его измеряют и подают на регулятор для сравнения с заданным значением и выработки управляющего сигнала, изменяющего значение входного сигнала (рисунок 1.4).
Рисунок 1.4 - Структурная схема САУ по возмущению При таком принципе управления изменение возмущающего воздействия компенсируется регулятором до того, как оно нарушит технологический режим работы объекта. Однако есть существенный недостаток – неспособность компенсировать влияние других возмущающих воздействий. САУ по возмущению является разомкнутой, т.е. без обратной связи по выходному сигналу. Комбинированные САУ совмещают оба закона управления и лишены многих недостатков рассмотренных схем (рисунок 1.5).
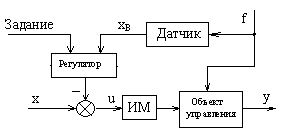
Рисунок 1.5 - Структурная схема комбинированной САУ По закону изменения выходного сигнала задатчика различают САУ стабилизации, программные и следящие. По закону изменения выходного сигнала регулятораразличают САУ дискретные (двух, трехпозиционные) и непрерывные (аналоговые). Двухпозиционные (вкл. – выкл.) САУ надежны (холодильные установки), дешевы, но мала точность регулирования. При рассмотрении САУ чаще используется укрупненная структурная схема (рисунке 4.2), на которой объект управления включает в себя регулирующий орган и датчик, а регулятор объединен с задатчиком и исполнительным механизмом. В ТАУ жетско организованную через цепочку элементов связи выходного сигнала системы с входным, при которой отклонение выходного сигнала системы (т.е. объекта) вызывает ссответствующее изменение ее входного сигнала, называют обратной связью (ОС). Различают о братную связь положительную и отрицательную. Отрицательная обратная связь– это связь выходного системы с входным, при которой отклонение выходного сигнала одного знака вызывает изменение входного сигнала противоположного знака. Например, при увеличении температуры выше заданной требуется уменьшить подачу топлива. Положительной обратной связью – это такая связь выходного сигнала системы с входным, при которой отклонение выходного сигнала одного знака вызывает изменение входного сигнала такого же знака. В промышленных САУ регулятор всегда включен в отрицательную обратную связь. Положительная обратная связь используется в электронике для повышения коэффициента усиления схем. Синтез САУ сводится к выбору типа регулятора, которые реализуют пять основных законов регулирования.
Классификация регуляторов
Пропорциональный (П-регулятор) с одним параметром настройки. Его ПФ совпадает с ПФ пропорционального типового динамического звена:
где К – коэффициент усиления. Коэффициенты, входящие в ПФ регуляторов, называются их параметры настройки. В конструкциях П-регуляторов коэффициент может изменяться в диапазоне от 0,1 до 40. Интегральный (астатический),или И-регулятор с одним параметром настройки. Его ПФ совпадает с ПФ астатического (интегрирующего) ТДЗ:
где Ти – время интегрирования. В некоторых конструкциях И-регулятора параметр настройки Ти может изменяться в диапазоне от 1 до 2000с. Пропорционально-интегральный, или ПИ-регулятор с двумя параметрами настройки. Это один из наиболее часто используемых в промышленных САУ типов регуляторов. Его ПФ следующая:
Параметрами настройки регуляторов этого типа являются коэффициент усиления К и время интегрирования Ти. ПФ включает в себя сумму его пропорциональной и интегральной составляющих, что соотвествует параллельно-согласованному соединению элементов, заложенному в структуре ПИ-регулятора. Следовательно, в случае отказа интегральной составляющей Пи-регулятор будет работать как П-регулятор, что повышает надежность его работы. Пропорционально-дифференциальныйили ПД-регулятор с двумя параметрами настройки. Его ПФ имеет вид
где Тд – время дифференцирования. В некоторых конструкциях ПД-регулятора параметр настройки Тд изменяется в диапазоне от 1 до 200 с.
т.е. этот регулятор имеет три параметра настройки: К – коэффициент усиления, Ти – время интегрирования, Тд – время дифференцирования.
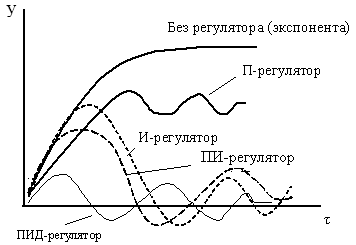
Рисунок 2.2 - Регулирование параметров объекта в системах с регуляторами различного типа.
Выбор типа регулятора или закона регулирования – трудная задача. Существуют ряд диаграмм и эмпирических формул, позволяющих по передаточной функции объекта определить необходимый тип регулятора и его оптимальные параметры настройки. Однако, на практике часто используются метод перебора: поочередно выбирают регулятор, проверяют на устойчивость и качество работы, и если полученные результаты неудовлетворительные, берут более сложный регулятор. Применение различных типов регуляторов проиллюстрировано на рисунке 2.3. Статический объект обладает свойством самовыравнивания, поэтому его регулируемый параметр без регулятора с течением времени по экспоненте приходит к постоянному значению. В САУ с П-регулятором имеется статическая ошибка, а в САУ с ПИД-регулятором (самым сложным и дорогим) – минимальные динамическая ошибка и время регулирования. В реальных промышленных САУ соединение элементов между собой может быть довольно сложным. Однако любую сложную схему можно разбить на отдельные блоки с одним из трех типовых соединений: последовательным, параллельно-согласованным или параллельно-встречным.
Тема 4. АФЧХ и ЛАЧХ Понятие об устойчивости
Под устойчивостью понимают способность системы самостоятельно приходить к последующему установившемуся состоянию после приложения воздействия, которое вывело ее из состояния равновесия. Исследование устойчивости является одной из основных задач в теории автоматического управления. Замкнутая система в силу свойств, обусловленных наличием обратной связи, склонна к неустойчивой работе. В процессе регулирования сигнал с выхода передается на вход группы звеньев системы, среди которых могут быть колебательные элементы. Приложение внешнего воздействия может привести к возмущенному состоянию системы, сопровождающемуся колебаниями регулируемой (выходной) величины. Наличие главной обратной связи будет способствовать поддержанию колебательного процесса и при больших коэффициентах усиления, если параметры системы не обеспечивают необходимого затухания энергии колебаний, может привести к неустойчивой работе, характеризуемой неограниченным возрастанием амплитуды колебаний. В устойчивых системах энергия колебаний с течением времени уменьшается, колебания затухают. Работа системы в переходном режиме описывается системой дифференциальных уравнений, на основании которых может быть написано одно-единственное дифференциальное уравнение. Его порядок определяется количеством и свойствами динамических звеньев. Понятие «устойчивость» в смысле его математической трактовки впервые в науку ввел русский ученый А.М.Ляпунов. Он дал строгую и законченную постановку задачи об устойчивости движения и методы ее решения. При исследовании устойчивости системы в общем случае приходится иметь дело с нелинейными задачами. Нелинейное дифференциальное уравнение, характеризующее возмущенное состояние системы, может быть разложено в ряд Тейлора и представлено в виде уравнения первого, второго или n-го приближения, содержащего величины первого, второго или n-го порядка малости. А.М.Ляпунов показал, что все случаи исследования устойчивости следует разделять на две категории: некритических (наиболее часто встречающихся) и критических случаев. Для категории некритических случаев справедливы две следующие теоремы. Теорема первая. Если вещественные части всех корней характеристического уравнения первого приближения отрицательны, то система будет устойчивой независимо от членов разложения выше первого порядка малости. Теорема вторая. Если среди корней характеристического уравнения первого приближения найдется по меньшей мере один с положительной вещественной частью, то система будет неустойчивой независимо от членов разложения выше первого порядка малости. Все критические случаи имеют место лишь тогда, когда среди корней характеристического уравнения первого приближения имеется некоторая группа корней, вещественная часть которых равна нулю, а остальная группа корней имеет отрицательную часть. В этом случае вопрос об устойчивости не может быть решен на основании исследования уравнений первого приближения. Поскольку уравнение первого приближения можно рассматривать как линеаризованное дифференциальное уравнение, то условия устойчивости А.М.Ляпунова справедливы и для линейных систем. Пусть, например, система описывается линейным дифференциальным уравнением n-го порядка
Решение этого уравнения:
где р1, р2, …рn – корни характеристического уравнения
Если система устойчива, то функция x(t) при t, стремящемся к бесконечности, будет приближаться к b/a0, что возможно лишь в том случае, если каждый из членов exp(pit) будет стремиться к нулю. Для этого все корни р1, р2, …рn должны иметь отрицательную вещественную часть. Корни характеристического уравнения можно представить в виде векторов, расположенных в комплексной плоскости (рисунок 5.1). Очевидно, что система будет устойчивой, если все корни располагаются слева от мнимой оси.
Рисунок 5.1 – Распределение корней в комплексной плоскости
В случае, если один вещественный корень или пара комплексно-сопряженных корней располагаются на мнимой оси, система оказывается на границе устойчивости. Системы, у которых имеется одна пара мнимых корней, могут совершать незатухающие колебания (автоколебания). Эти системы часто относят к неустойчивым, так как они практически неработоспособны. Линейные системы, характеристические уравнения которых имеют один нулевой корень при всех остальных корнях, расположенных левее мнимой оси, называют нейтрально-устойчивыми. Для того чтобы все корни оказались в левой полуплоскости, можно воздействовать на коэффициенты характеристического уравнения, которые, согласно теореме Виета, связаны с корнями непрерывными зависимостями. При исследовании устойчивости системы возможно решение следующих задач: - выяснение, является ли устойчивой система при заданных параметрах; - определение допустимых изменений некоторых параметров (при неизменных остальных параметрах и заданной структуре) без нарушения устойчивости системы; - анализ структуры системы и определение параметров, при которых она может стать устойчивой (анализ структурной устойчивости). Первая задача может быть решена различными методами. Можно определить корни характеристического уравнения и по ним установить знаки их вещественных частей. Однако такой метод может быть использован, когда порядок характеристического уравнения ниже третьего. Уже для кубического уравнения трудно определить корни, не говоря об уравнениях более высоких порядков. Кроме того, для определения устойчивости совершенно не обязательно знать значение корней характеристического уравнения. Достаточно убедиться только в отрицательности вещественных частей корней. Поэтому представляется целесообразным воспользоваться другими, более простыми методами определения устойчивости, основанными на установлении факта отрицательности вещественных частей корней без нахождения их значения. Такие методы основываются на использовании критериев устойчивости, например алгебраических критериев Рауса и Гурвица, частотных критериев Михайлова и Найквиста, а также условий устойчивости, определяемых логарифмическими частотными характеристиками. Для решения второй задачи могут быть использованы методы выделения областей устойчивости.
5 .2 Алгебраические критерии устойчивости
5.2.1 Критерий Рауса
Алгебраические критерии устойчивости позволяют установить, устойчива система или нет, по результатам алгебраических действий над коэффициентами характеристического уравнения. Условия, устанавливающие факт отрицательности вещественных частей корней, и будут являться критериями устойчивости. Впервые подобный критерий был предложен английским математиком Э.Раусом в 1877 году в виде алгоритма. Пусть дано характеристическое уравнение а0 рn + a1 pn-1 +... + an-1 p + an =0. (5.4)
В первой строке таблицы Рауса записывают в порядке возрастания индексы коэффициентов характеристического уравнения (6.4), имеющие четный порядок: а0 а2 а4 а6 … Во второй строке коэффициенты с нечетным порядком: а1 а3 а5 а7... Остальные строки состоят из элементов, определяемых по формуле Ck,i = Ck+1,i-2 – ri Ck+1,i-1 (5.5) ri = C1,i-2 / C1,i-1 (5.6) где k – номер столбца; i – номер строки. Число строк таблицы Рауса равно (n +1). Коэффициенты критерия Рауса сведены в таблицу 5.1. Таблица 5.1 - Коэффициенты критерия Рауса
Критерий Рауса: для того, чтобы система была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т.е. при а0>0 были положительными: С11 = а0 >0; C12 = a1 >0; C13 >0;..... C1,n+1 >0 (5.7)
5.2.2 Критерий Гурвица
В 1895 году немецкий математик Гурвиц А. предложил следующий метод: из коэффициентов характеристического уравнения (5.4) сначала строят главный определитель
Главный определитель составляется так, что по главной диагонали выписываются коэффициенты уравнения начиная с а1 в возрастающем порядке до аn. От каждого коэффициента главной диагонали по вертикали вверх выписываются коэффициенты с возрастающими и вниз - с убывающими индексами. Места в матрице коэффициентов с индексами больше n и меньше 0 заполняются нулями. Вещественные части корней будут отрицательными в том случае, если все коэффициенты уравнения и диагональные миноры главного определителя будут положительными. Отчеркивая в главном определителе Гурвица диагональные миноры, получаем определители Гурвица низшего порядка:
Критерий Гурвица: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки, одинаковые со знаком первого коэффициента а0 характеристического уравнения, т.е. при а 0 >0 были положительными
Обычно критерий Гурвица применяется для систем с n ≤ 4, выше используется критерий Льенара – Шипара. В последнем столбце главного определителя (6.8) отличен от нуля только аn, поэтому Δn = an Δn-1. (5.10) Поэтому для проверки устойчивости САУ достаточно найти Δ1 – Δn-1. Если все определители Δ1 – Δn-1 >0, а главный Δn = 0, то САУ находится на границе устойчивости. Это возможно только в двух случаях: an = 0 или Δn-1 >0. В первом (an = 0) САУ находится на границе апериодической устойчивости (один из корней si = 0); во втором (Δn-1 >0) на границе колебательной устойчивости (2 комплексно-сопряженных корня находятся на мнимой оси si = jωi; si+1 = -jωi). Для систем, имеющих характеристические уравнения n ≥ 5 удобно применять одну из модификаций критерия Гурвица, предложенную в в 1914 году Льенаром П. и Шипаром Р.: для того чтобы САУ была устойчива, необходимо и достаточно, чтобы выполнялись неравенства a0 >0, a1 >0,..........an >0 (5.11) Δ1 >0, Δ3 >0, Δ5 >0......... – нечетные определители или a0 >0, a1 >0,..........an >0 (5.12) Δ2 >0, Δ4 >0, Δ6 >0......... – четные определители Очевидно, что этот критерий требует в два раза меньше раскрытий определителей, чем критерий Гурвица, поэтому особенно удобен при исследовании устойчивости САУ высшего порядка. Рассмотрим выражение критерия Гурвица для некоторых уравнений. Уравнение третьего порядка a0 р3 +а1 р2 +а2 р + а3 = 0. Главный определитель
Условие Гурвица (а1 а2 –а0 а3) > 0, а3 (а1 а2 – а0 а3) > 0, ai > 0, i = 1, 2, 3. Следовательно, система будет устойчивой, если все коэффициенты а0,а1,a2,а3 положительны и а1a2 – a0a3 >0, т.е. а1a2 > a0a3. Для уравнений третьего порядка при положительных коэффициентах а0,а1,a2,а3 и выполнения условия а1a2 > a0a3 называется критерием устойчивости Вышнеградского. Уравнение четвертого порядка а0 р4 +al p3 +a2 p2 + а3 р + а4 = 0. Главный определитель
Условия Гурвица
или Δ3 = а3(а1а2 - а0а3) – а12 а4 = а3 Δ2 – а12 а4 >0. Определитель Δ3 может быть положительным лишь при условии Δ2 > 0. Поэтому условие устойчивости для уравнения четвертого порядка может быть выражено соотношением а3 (а1а2 –a3 a0) – а12 а4 > 0. Уравнение пятого порядка а0р5 + а1р4 +а2р3 +а3р2 +а4р + а5 = 0. Система, описываемая уравнением пятого порядка, устойчива, если Δ3 = а1(а2а3 – а1а4) – а0а32 >0. Δ4 = (a3a4 -а2а5)(а1а2 -а0а3)- (а1а4 -а0а5)2 > 0. Примеры: D(s) = 12S4 + 2S2 +4S + 50 = 0 - система неустойчива, т.к. а1 = 0. D(s) = 3S5 +10S4 + 5S3 - 7S2 +S + 10 = 0 - система неустойчива, т.к. а3 = -7<0. D(s) = 2S3 + 6S2 +10S + 15 = 0 - система устойчива, т.к. а1a2 > a0a3 или 6 ∙ 10>2 ∙ 15
Критерий Найквиста
Критерий Найквиста, основанный на использовании частотных характеристик, позволяет судить об устойчивости замкнутой САУ по ее амплитудно-фазовой характеристике в разомкнутом состоянии. Установим связь между п.ф. одноконтурной системы в замкнутом и разомкнутом состояниях. Рассмотрим функцию
где числитель представляет характеристический полином системы в замкнутом состоянии, а знаменатель — характеристический полином разомкнутой по цепи главной обратной связи системы. Выражение
есть передаточная функция разомкнутой системы. Так как порядок полинома D(p) для физически реализуемых систем не должен превышать порядок полинома G(p), то характеристическое уравнение замкнутой системы G(p) + D(p) = 0 (6.3) имеет столько же корней, сколько и характеристическое уравнение разомкнутой системы G(p) = 0. (6.4) При выводе критерия Найквиста будем исходить из того, что система устойчива как в замкнутом, так и в разомкнутом состоянии, т.е. вещественные части корней уравнений (6.3) и (6.4) отрицательны. Заменив в уравнении (7.1) р на jω и разложив числитель и знаменатель на простейшие множители, получим уравнение амплитудно-фазовой характеристики замкнутой системы:
где р1, р2,..., рm; s1, s2,..., sm — соответственно корни уравнении (6.3) и (6.4).
Множители числителя и знаменателя правой части выражения (7.5) представляют векторы, располагаемые в комплексной плоскости слева от мнимой оси (рисунок 6.1, а). Начало каждого вектора лежит в точке, соответствующей корню уравнения рк, а конец — на мнимой оси. При изменении частоты ω от -∞ до +∞ каждый из векторов повернется на угол π. Числитель выражения (6.5) представляет вектор, модуль которого А равен произведению модулей перемножаемых векторов, а аргумент φА — сумме аргументов тех же т векторов. Поэтому при изменении ω от - ∞ до +∞ результирующий вектор D(jω) + G(jω) повернется на угол φА = mπ. Так как по условию корни G(p) = 0 лежат слева от мнимой оси, угол поворота φВ результирующего вектора, имеющего модуль В, при изменении ω от - ∞ до +∞ также будет равен mπ. Нетрудно заключить поэтому, что угол поворота вектора 1 + W(jω) при изменении ω от - ∞ до +∞ равен φА - φВ = mπ – mπ = 0. (6.6)
Рисунок 6.1 - Пояснения критерия Найквиста: а) расположение векторов р-pi в комплексной плоскости; б) АФХ разомкнутой системы
Амплитудно-фазовая характеристика (АФХ) разомкнутой системы получается путем замены р на jω в уравнении (6.2):
Она отображает границу области устойчивости. При ω→0 W(jω)→an/bm, а при ω→∞ W(jω)→0, если порядок числителя меньше порядка знаменателя (n<m), и W(jω)→а0/b0 при равенстве порядков числителя и знаменателя (n= m). Амплитудно-фазовая характеристика при изменении ω от - ∞ до +∞ симметрична относительно оси абсцисс (рисунок 6.1, б). Если из точки с координатами (-1; j0) провести вектор, который своим концом касается амплитудно-фазовой характеристики, то получим вектор 1 + W(jω), так как О1А = ОА - (-1) = 1 + ОА = 1 + W(jω). При изменении ω от - ∞ до +∞ конец вектора 1 + W(jω) будет скользить по амплитудно-фазовой характеристике, а сам вектор повернется на угол, результирующее значение которого равно нулю. Последнее возможно, если точка (-1;j0) лежит вне амплитудно-фазовой характеристики. Это условие согласуется с условием (2.6), которое возможно лишь в случае, когда система устойчива. Первый критерий Найквиста: замкнутая система будет устойчивой в том случае, если устойчива разомкнутая система и ее амплитудно-фазовая характеристика не охватывает точку (-1; j0). Кривая (рисунок 6.1,б), представляющая частотную характеристику устойчивой системы, пересекается с осью абсцисс справа от точки (-1;jО) и называется амплитудно-фазовой характеристикой первого рода. Кривая (рисунок 7.2,а), пересекающаяся с осью абсцисс и справа, и слева от точки (-1;jО), называется амплитудно-фазовой характеристикой второго рода. В этом случае система в замкнутом состоянии будет устойчивой при условии, если, разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов амплитудно-фазовой характеристики через ось абсцисс слева от точки (-1;jО) равна нулю.
Рисунок 6.2 - Исследование устойчивости по АФХ: а) АФХ второго рода; б) определение запаса устойчивости по модулю и фазе
При анализе устойчивости системы по амплитудно-фазовым характеристикам целесообразно ввести понятие запаса устойчивости по модулю и по фазе. Если через точку (-1;jО) (рисунок 7.2,б) провести окружность единичного радиуса, получим точку пересечения ее с амплитудно-фазовой характеристикой (точка А). Запас устойчивости по модулю характеризуется отрезком h, а запас устойчивости по фазе — углом γ. В общем случае, если степень полинома D(jω) в уравнении (7.7) меньше степени полинома G(jω) и они не имеют общих корней с неотрицательной вещественной частью, критерий Найквиста формулируется следующим образом: САУ, неустойчивая в разомкнутом состоянии, является устойчивой в замкнутом состоянии, если разность между числам положительных и отрицательных переходов АФХ через ось абсцисс слева от точки (-1;j0) равна r/2. Сформулированный ранее критерий устойчивости Найквиста следует рассматривать как частный случай общей задачи при r = 0 (r – число правых корней характеристического уравнения разомкнутой системы).
Критерий Михайлова
Критерий Михайлова дает возможность судить об устойчивости системы по годографу, описываемому концом характеристического вектора замкнутой системы, который может быть получен из уравнения (6.3): М(р) = D(p) + G(p). (6.8) Если заменить р на jω и изменять ω от 0 до ∞, то вектор своим концом опишет в комплексной плоскости кривую, называемую годографом Михайлова. Выражение (6.8) представляет полином m-го порядка, который может быть разложен (при р = jω) на множители по теореме Безу: М(jω) = (jω – p1)(jω – p2)…(jω – рm), (6.9) где р1, р2, …,рm – корни уравнения (6.3). Уравнение (6.9) написано в предположении, что замкнутая система устойчива. Правая часть этого уравнения представляет произведение векторов, расположенных слева от мнимой оси в плоскости корней (рисунок 6.3,а). Так как векторы (jω – pk), соответствующие вещественным корням, совпадают с осью абсцисс, то при изменении ω от 0 до ∞ каждый из них повернется на угол π/2. Каждая же пара комплексно-сопряженных корней повернется при этом на угол π. Действительно, вектор (jω – р2) при изменении ω от 0 до ∞ повернется на угол α1, а вектор (jω – р3) на угол α2. Так как ∟ABO = ∟BAO = α2 (ΔOAB — равнобедренный), то результирующий угол поворота обоих векторов α1 + α2 = π. Таким образом, вектор М(jω), представляющий произведение m векторов, аргументы которых при умножении складываются, повернется при этих условиях на угол m(π/2). При ω=0 годограф Михайлова отсекает на вещественной оси в положительном направлении отрезок, равный свободному члену характеристического уравнения. Начало характеристического вектора совпадает с началом координат. Поэтому, если система устойчива, характеристический вектор при своем вращении нигде не должен обращат
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 4534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.28.79 (0.013 с.) |







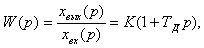

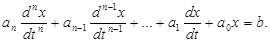 (5.1)
(5.1) (5.2)
(5.2)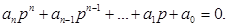 (5.3)
(5.3)
 (5.8)
(5.8)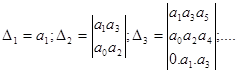
 (5.9)
(5.9)
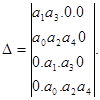


 (6.1)
(6.1) (6.2)
(6.2) (6.5)
(6.5)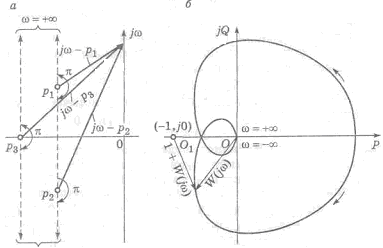
 (6.7)
(6.7)



